#include <circles.h>

Collaboration diagram for TCluster:

Public Member Functions
	TCluster (PGraphAttributes GraphAttributes, TInt K, TFlt Lambda)
	~TCluster ()
void	Train (TInt OuterReps, TInt GradientReps, TInt MCMCReps)
	Train the model to predict K Clusters.
TVec< TIntSet >	GetCircles (void)
Public Attributes
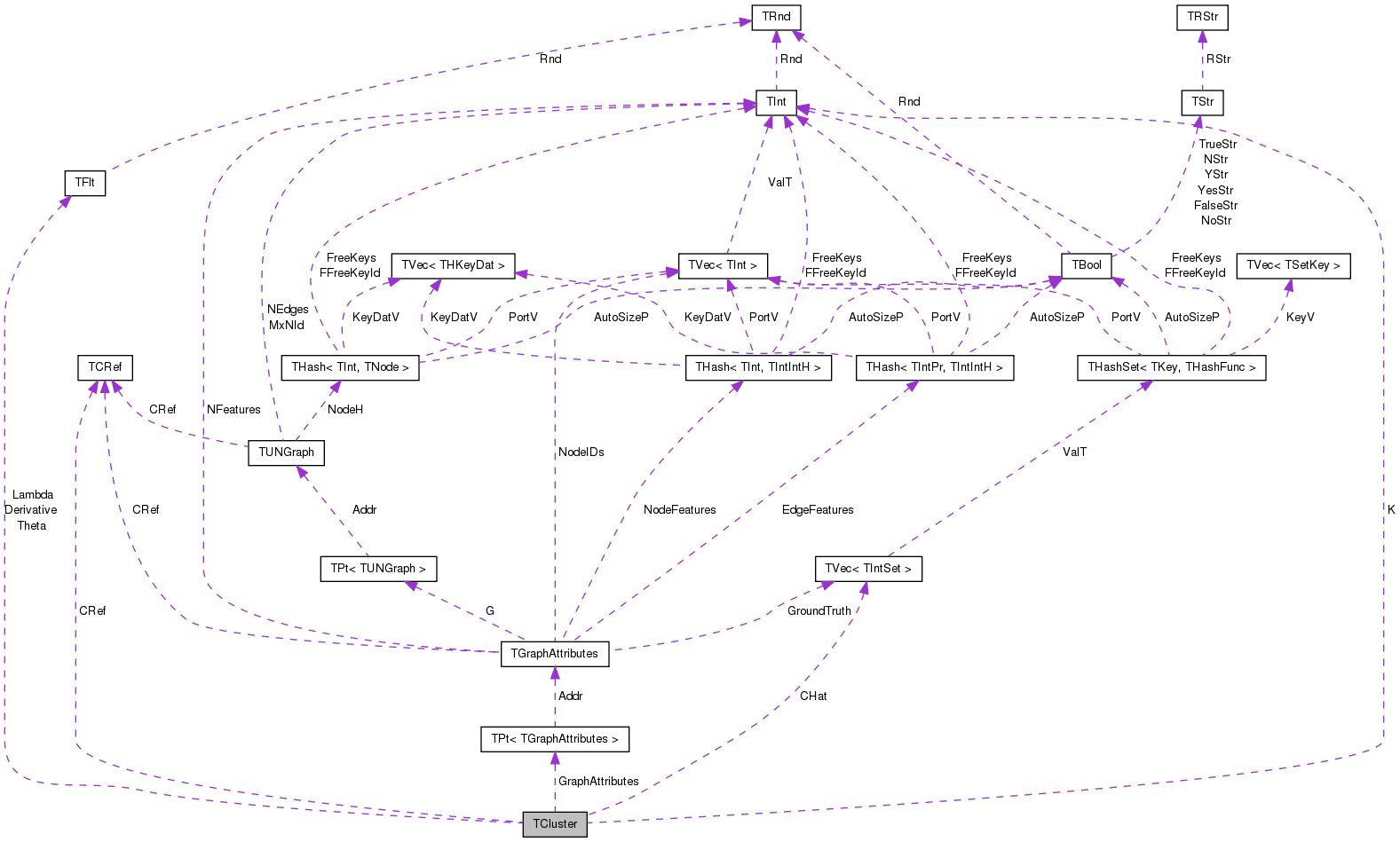
TCRef	CRef
Private Member Functions
TFlt	LogLikelihood ()
	Compute the log-likelihood of Parameters and cluster assignments.
TIntSet	MCMC (TInt k, TInt MCMCReps)
	Optimize the cluster assignments for the k'th cluster.
void	Gradient ()
	Update partial derivatives of log-likelihood.
Private Attributes
TFlt *	Theta
TFlt *	Derivative
TVec< TIntSet >	CHat
PGraphAttributes	GraphAttributes
TInt	K
TFlt	Lambda

Detailed Description

Definition at line 28 of file circles.h.

Constructor & Destructor Documentation

TCluster::TCluster	(	PGraphAttributes	GraphAttributes,
		TInt	K,
		TFlt	Lambda
	)		`[inline]`

Parameters:

GraphAttributes	attributed graph object with attributes
K	number of communities to detect
Lambda	regularization parameter

Definition at line 35 of file circles.h.

References TVec< TVal, TSizeTy >::Add(), CHat, Derivative, K, TGraphAttributes::NFeatures, and Theta.

                                                                  :
    GraphAttributes(GraphAttributes), K(K), Lambda(Lambda) {
    Theta = new TFlt[K * GraphAttributes->NFeatures];
    Derivative = new TFlt[K * GraphAttributes->NFeatures];
    for (int k = 0; k < K; k++) {
      for (int f = 0; f < GraphAttributes->NFeatures; f++) {
        Theta[k * GraphAttributes->NFeatures + f] = 0;
        Derivative[k * GraphAttributes->NFeatures + f] = 0;
      }

      // Clusters are initially empty.
      CHat.Add(TIntSet());
    }
  }

Here is the call graph for this function:

TCluster::~TCluster ( ) [inline]

Definition at line 49 of file circles.h.

References Derivative, and Theta.

              {
    delete[] Theta;
    delete[] Derivative;
  }

Member Function Documentation

TVec<TIntSet> TCluster::GetCircles ( void ) [inline]

Returns:: the predicted circles

Definition at line 64 of file circles.h.

References CHat.

                                 {
    return CHat;
  }

void TCluster::Gradient ( void ) [private]

Update partial derivatives of log-likelihood.

Definition at line 456 of file circles.h.

References THash< TKey, TDat, THashFunc >::BegI(), CHat, Derivative, TGraphAttributes::EdgeFeatures, TGraphAttributes::G, THashKeyDatI< TKey, TDat >::GetDat(), GraphAttributes, Inner(), TUNGraph::IsEdge(), THashKeyDatI< TKey, TDat >::IsEnd(), K, Lambda, TGraphAttributes::NFeatures, Theta, TPair< TVal1, TVal2 >::Val1, and TPair< TVal1, TVal2 >::Val2.

Referenced by Train().

                            {
  for (int i = 0; i < K * GraphAttributes->NFeatures; i++) {
    if (Theta[i] > 0) {
      Derivative[i] = -Lambda * Theta[i];
    } else {
      Derivative[i] = Lambda * Theta[i];
    }
  }

  for (THashKeyDatI<TIntPr, TIntIntH> it = GraphAttributes->EdgeFeatures.BegI();
       not it.IsEnd(); it++) {
    TFlt InnerProduct = 0;
    TIntPr Edge = it.GetKey();
    TInt Src = Edge.Val1;
    TInt Dst = Edge.Val2;
    TBool Exists = GraphAttributes->G->IsEdge(Src, Dst);
    for (int k = 0; k < K; k++) {
      TFlt d = CHat[k].IsKey(Src) and CHat[k].IsKey(Dst) ? 1 : -1;
      InnerProduct += d * Inner(it.GetDat(), Theta + k * GraphAttributes->NFeatures);
    }
    TFlt expinp = exp(InnerProduct);
    TFlt q = expinp / (1 + expinp);
    if (q != q) {
      q = 1; // Test for nan in case of overflow.
    }

    for (int k = 0; k < K; k++) {
      TBool d_ = CHat[k].IsKey(Src) and CHat[k].IsKey(Dst);
      TFlt d = d_ ? 1 : -1;
      for (THashKeyDatI<TInt, TInt> itf = it.GetDat().BegI();
           not itf.IsEnd(); itf++) {
        TInt i = itf.GetKey();
        TInt f = itf.GetDat();
        if (Exists) {
          Derivative[k * GraphAttributes->NFeatures + i] += d * f;
        }
        Derivative[k * GraphAttributes->NFeatures + i] += -d * f * q;
      }
    }
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

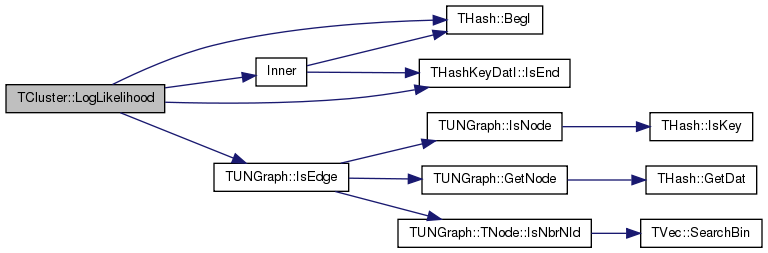
TFlt TCluster::LogLikelihood ( void ) [private]

Compute the log-likelihood of Parameters and cluster assignments.

Returns:: the log-likelihood of the current model

Definition at line 499 of file circles.h.

References THash< TKey, TDat, THashFunc >::BegI(), CHat, TGraphAttributes::EdgeFeatures, TGraphAttributes::G, GraphAttributes, Inner(), TUNGraph::IsEdge(), THashKeyDatI< TKey, TDat >::IsEnd(), K, TGraphAttributes::NFeatures, Theta, TPair< TVal1, TVal2 >::Val1, and TPair< TVal1, TVal2 >::Val2.

Referenced by Train().

                                 {
  TFlt ll = 0;
  for (THashKeyDatI<TIntPr, TIntIntH> it = GraphAttributes->EdgeFeatures.BegI();
       not it.IsEnd(); it++) {
    TFlt InnerProduct = 0;
    TIntPr Edge = it.GetKey();
    TInt Src = Edge.Val1;
    TInt Dst = Edge.Val2;
    TBool Exists = GraphAttributes->G->IsEdge(Src, Dst);

    for (int k = 0; k < K; k++) {
      TFlt d = CHat[k].IsKey(Src) and CHat[k].IsKey(Dst) ? 1 : -1;
      InnerProduct += d * Inner(it.GetDat(), Theta + k * GraphAttributes->NFeatures);
    }
    if (Exists) {
      ll += InnerProduct;
    }
    TFlt ll_ = log(1 + exp(InnerProduct));
    ll += -ll_;
  }

  if (ll != ll) {
    printf("ll isnan\n");
    exit(1);
  }
  return ll;
}

Here is the call graph for this function:

Here is the caller graph for this function:

TIntSet TCluster::MCMC	(	TInt	k,
		TInt	MCMCReps
	)		`[private]`

Optimize the cluster assignments for the k'th cluster.

Parameters:

k	community index on which to run MCMC
MCMCReps	number of iterations of MCMC

Returns:: node ids for the updated community

Definition at line 358 of file circles.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), THashSet< TKey, THashFunc >::AddKey(), THash< TKey, TDat, THashFunc >::BegI(), CHat, TGraphAttributes::EdgeFeatures, TGraphAttributes::G, THash< TKey, TDat, THashFunc >::GetDat(), THash< TKey, TDat, THashFunc >::GetKeyId(), TRnd::GetUniDev(), GraphAttributes, Inner(), TUNGraph::IsEdge(), THashKeyDatI< TKey, TDat >::IsEnd(), K, TVec< TVal, TSizeTy >::Len(), TGraphAttributes::NFeatures, TGraphAttributes::NodeIDs, Theta, TPair< TVal1, TVal2 >::Val1, and TPair< TVal1, TVal2 >::Val2.

Referenced by Train().

                                            {
  TRnd t;

  THash<TInt, TFlt> CostNotIncludeHash;
  THash<TInt, TFlt> CostIncludeHash;

  TVec<TInt> NewLabel;
  int csize = 0;
  for (int i = 0; i < GraphAttributes->NodeIDs.Len(); i++) {
    if (CHat[k].IsKey(GraphAttributes->NodeIDs[i])) {
      NewLabel.Add(0);
    } else {
      NewLabel.Add(1);
    }
    if (CHat[k].IsKey(GraphAttributes->NodeIDs[i])) {
      csize++;
    }
  }
  // Compute edge log-probabilities.
  for (THashKeyDatI<TIntPr, TIntIntH> it = GraphAttributes->EdgeFeatures.BegI();
       not it.IsEnd(); it++) {
    TIntPr e = it.GetKey();
    TInt kv = GraphAttributes->EdgeFeatures.GetKeyId(e);
    TInt Src = e.Val1;
    TInt Dst = e.Val2;

    TBool Exists = GraphAttributes->G->IsEdge(Src, Dst);
    TFlt InnerProduct = Inner(it.GetDat(), Theta + k * GraphAttributes->NFeatures);
    TFlt Other = 0;
    for (int l = 0; l < K; l++) {
      if (l == k) {
        continue;
      }
      TFlt d = (CHat[l].IsKey(Src) and CHat[l].IsKey(Dst)) ? 1 : -1;
      Other += d * Inner(it.GetDat(), Theta + l * GraphAttributes->NFeatures);
    }

    TFlt CostNotInclude;
    TFlt CostInclude;

    if (Exists) {
      CostNotInclude = -Other + InnerProduct + log(1 + exp(Other - InnerProduct));
      CostInclude = -Other - InnerProduct + log(1 + exp(Other + InnerProduct));
    } else {
      CostNotInclude = log(1 + exp(Other - InnerProduct));
      CostInclude = log(1 + exp(Other + InnerProduct));
    }

    CostNotIncludeHash.AddDat(kv) = -CostNotInclude;
    CostIncludeHash.AddDat(kv) = -CostInclude;
  }

  // Run MCMC using precomputed probabilities
  TFlt InitialTemperature = 1.0; // Initial temperature
  for (int r = 2; r < MCMCReps + 2; r++) {
    TFlt Temperature = InitialTemperature / log(r);
    for (int n = 0; n < GraphAttributes->NodeIDs.Len(); n++) {
      TFlt l0 = 0;
      TFlt l1 = 0;
      for (int np = 0; np < GraphAttributes->NodeIDs.Len(); np++) {
        if (n == np) {
          continue;
        }
        TIntPr ed(GraphAttributes->NodeIDs[n], GraphAttributes->NodeIDs[np]);
        if (ed.Val1 > ed.Val2) {
          ed = TIntPr(ed.Val2, ed.Val1);
        }
        TInt kv = GraphAttributes->EdgeFeatures.GetKeyId(ed);
        TFlt m0 = CostNotIncludeHash.GetDat(kv);
        if (NewLabel[np] == 0) {
          l0 += m0;
          l1 += m0;
        } else {
          l0 += m0;
          l1 += CostIncludeHash.GetDat(kv);
        }
      }
      TFlt LogLikelihoodDiff = exp(l1 - l0);
      TFlt AcceptProb = pow(LogLikelihoodDiff, 1.0 / Temperature);
      if (t.GetUniDev() < AcceptProb) {
        NewLabel[n] = 1;
      } else {
        NewLabel[n] = 0;
      }
    }
  }

  TIntSet Result;
  for (int i = 0; i < GraphAttributes->NodeIDs.Len(); i++) {
    if (NewLabel[i]) {
      Result.AddKey(GraphAttributes->NodeIDs[i]);
    }
  }

  return Result;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TCluster::Train	(	TInt	OuterReps,
		TInt	GradientReps,
		TInt	MCMCReps
	)

Train the model to predict K Clusters.

Parameters:

OuterReps	number of coordinate ascent iterations
GradientReps	number of iterations of gradient ascent
MCMCReps	number of iterations of MCMC

Definition at line 292 of file circles.h.

References CHat, TVec< TVal, TSizeTy >::Clr(), Derivative, TRnd::GetUniDevInt(), Gradient(), GraphAttributes, K, TVec< TVal, TSizeTy >::Len(), LogLikelihood(), MCMC(), TGraphAttributes::NFeatures, TGraphAttributes::NodeIDs, and Theta.

                                                                     {
  // Learning rate
  TFlt Increment = 1.0 / (1.0 * GraphAttributes->NodeIDs.Len() * GraphAttributes->NodeIDs.Len());
  TRnd t;

  for (int OuterRep = 0; OuterRep < OuterReps; OuterRep++) {
    // If it's the first iteration or the solution is degenerate,
    // randomly initialize the weights and Clusters
    for (int k = 0; k < K; k++) {
      if (OuterRep == 0 or CHat[k].Empty() or CHat[k].Len()
          == GraphAttributes->NodeIDs.Len()) {
        CHat[k].Clr();
        for (int i = 0; i < GraphAttributes->NodeIDs.Len(); i++) {
          if (t.GetUniDevInt(2) == 0) {
            CHat[k].AddKey(GraphAttributes->NodeIDs[i]);
          }
        }
        for (int i = 0; i < GraphAttributes->NFeatures; i++) {
          Theta[k * GraphAttributes->NFeatures + i] = 0;
        }
        // Just set a single Feature to 1 as a random initialization.
        Theta[k * GraphAttributes->NFeatures + t.GetUniDevInt(GraphAttributes->NFeatures)] = 1.0;
        Theta[k * GraphAttributes->NFeatures] = 1;
      }
    }
    
    for (int k = 0; k < K; k++) {
      CHat[k] = MCMC(k, MCMCReps);
    }
    TFlt llPrevious = LogLikelihood();

    // Perform gradient ascent
    TFlt ll = 0;
    for (int gradientRep = 0; gradientRep < GradientReps; gradientRep++) {
      Gradient();
      for (int i = 0; i < K * GraphAttributes->NFeatures; i++) {
        Theta[i] += Increment * Derivative[i];
      }
      printf(".");
      fflush( stdout);
      ll = LogLikelihood();

      // If we reduced the objective, undo the update and stop.
      if (ll < llPrevious) {
        for (int i = 0; i < K * GraphAttributes->NFeatures; i++) {
          Theta[i] -= Increment * Derivative[i];
        }
        ll = llPrevious;
        break;
      }
      llPrevious = ll;
    }
    printf("\nIteration %d, ll = %f\n", OuterRep + 1, (double) ll);
  }
}