#include <linalg.h>

Static Public Member Functions
static void	SimpleLanczos (const TMatrix &Matrix, const int &NumEig, TFltV &EigValV, const bool &DoLocalReortoP=false, const bool &SvdMatrixProductP=false)
static void	Lanczos (const TMatrix &Matrix, int NumEig, int Iters, const TSpSVDReOrtoType &ReOrtoType, TFltV &EigValV, TFltVV &EigVecVV, const bool &SvdMatrixProductP=false)
static void	Lanczos2 (const TMatrix &Matrix, int MaxNumEig, int MaxSecs, const TSpSVDReOrtoType &ReOrtoType, TFltV &EigValV, TFltVV &EigVecVV, const bool &SvdMatrixProductP=false)
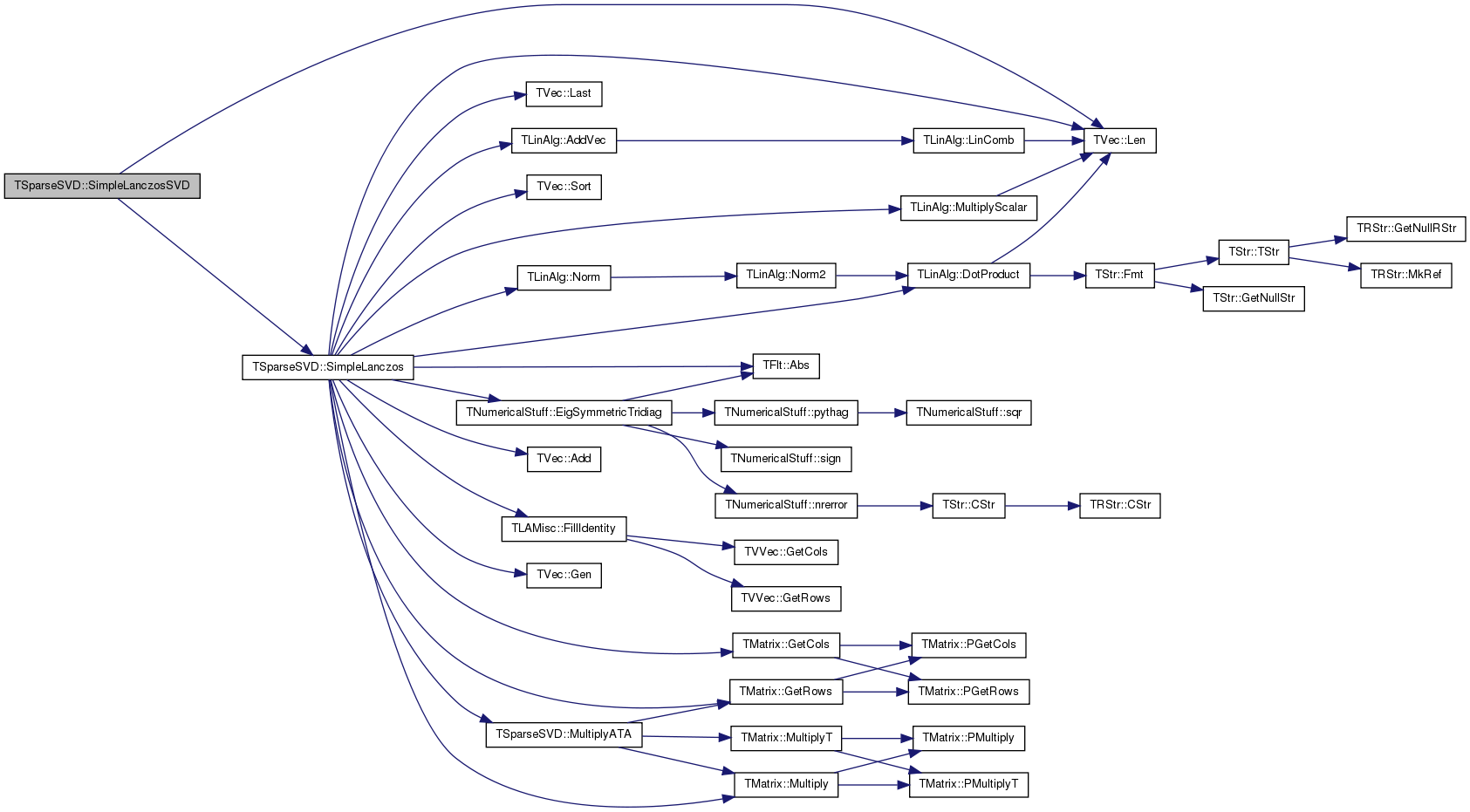
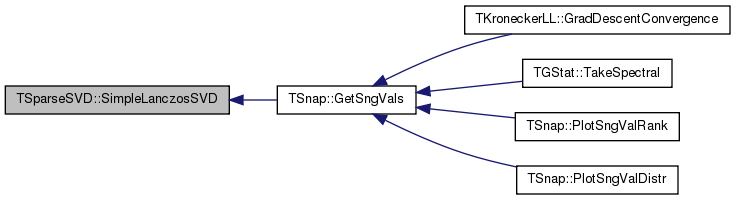
static void	SimpleLanczosSVD (const TMatrix &Matrix, const int &CalcSV, TFltV &SngValV, const bool &DoLocalReortoP=false)
static void	LanczosSVD (const TMatrix &Matrix, int NumSV, int Iters, const TSpSVDReOrtoType &ReOrtoType, TFltV &SgnValV, TFltVV &LeftSgnVecVV, TFltVV &RightSgnVecVV)
static void	OrtoIterSVD (const TMatrix &Matrix, int NumSV, int IterN, TFltV &SgnValV)
static void	Project (const TIntFltKdV &Vec, const TFltVV &U, TFltV &ProjVec)
Static Private Member Functions
static void	MultiplyATA (const TMatrix &Matrix, const TFltVV &Vec, int ColId, TFltV &Result)
static void	MultiplyATA (const TMatrix &Matrix, const TFltV &Vec, TFltV &Result)

Detailed Description

Definition at line 405 of file linalg.h.

Member Function Documentation

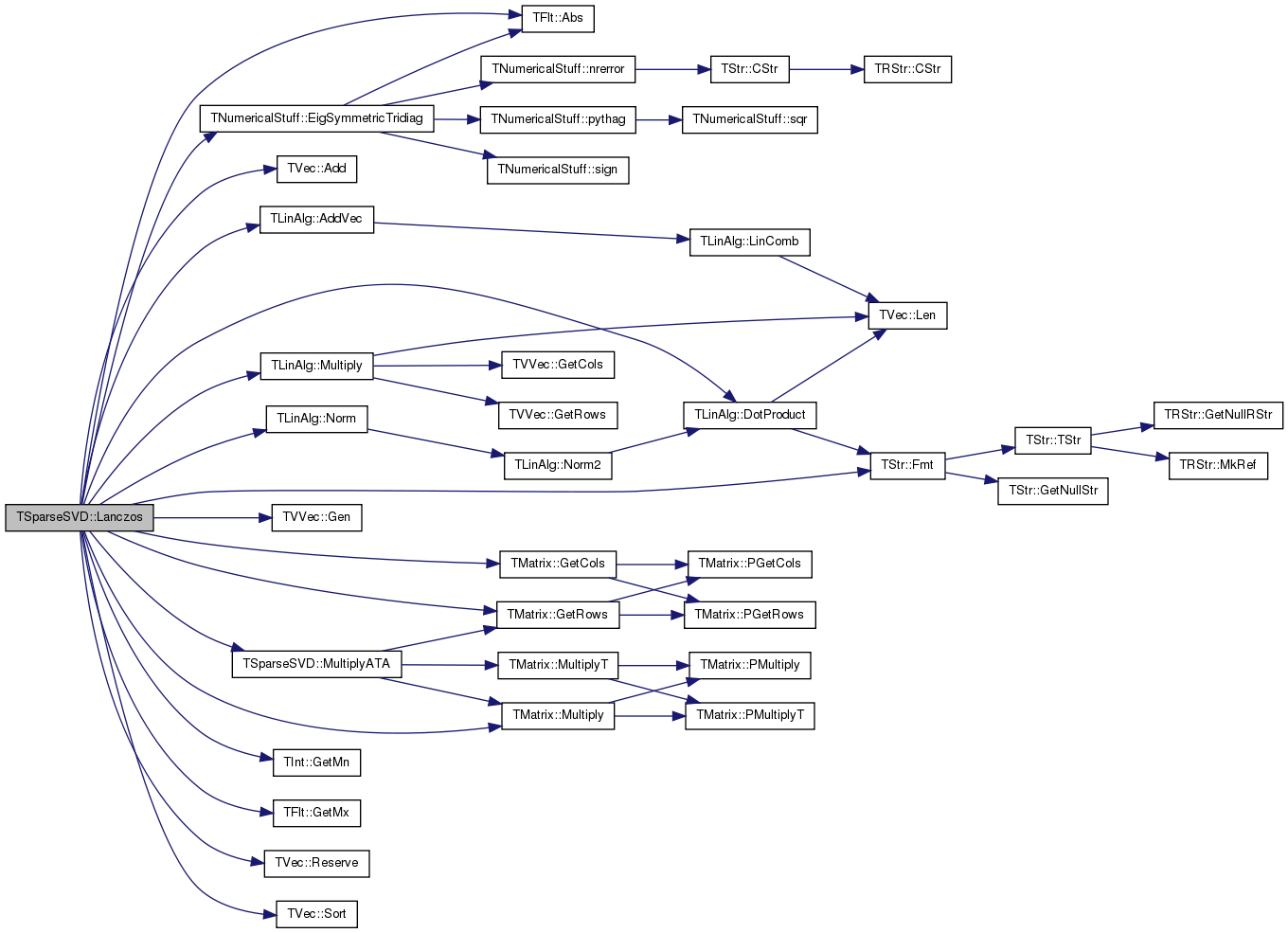
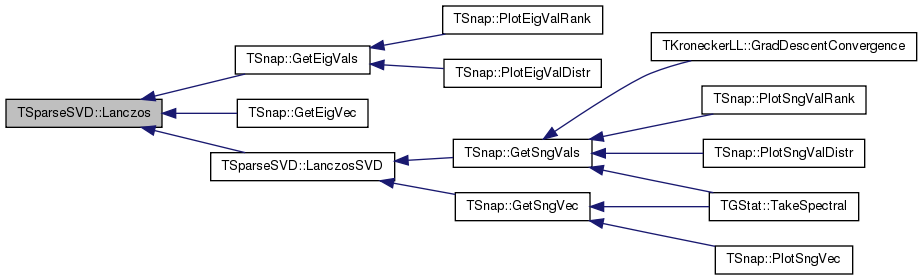
void TSparseSVD::Lanczos	(	const TMatrix &	Matrix,
		int	NumEig,
		int	Iters,
		const TSpSVDReOrtoType &	ReOrtoType,
		TFltV &	EigValV,
		TFltVV &	EigVecVV,
		const bool &	SvdMatrixProductP = `false`
	)		`[static]`

Definition at line 1123 of file linalg.cpp.

References TFlt::Abs(), TVec< TVal >::Add(), TLinAlg::AddVec(), TLinAlg::DotProduct(), TNumericalStuff::EigSymmetricTridiag(), TStr::Fmt(), TVVec< TVal >::Gen(), TMatrix::GetCols(), TInt::GetMn(), TFlt::GetMx(), TMatrix::GetRows(), IAssert, IAssertR, TMatrix::Multiply(), TLinAlg::Multiply(), MultiplyATA(), TLinAlg::Norm(), TVec< TVal >::Reserve(), TVec< TVal >::Sort(), ssotFull, and ssotSelective.

Referenced by TSnap::GetEigVals(), TSnap::GetEigVec(), and LanczosSVD().

                                                                         {

    if (SvdMatrixProductP) {
        // if this fails, use transposed matrix
        IAssert(Matrix.GetRows() >= Matrix.GetCols());
    } else {
        IAssert(Matrix.GetRows() == Matrix.GetCols());
    }
  IAssertR(NumEig <= Iters, TStr::Fmt("%d <= %d", NumEig, Iters));

    //if (ReOrtoType == ssotFull) printf("Full reortogonalization\n");
    int i, N = Matrix.GetCols(), K; // K - current dimension of T
    double t = 0.0, eps = 1e-6; // t - 1-norm of T

    //sequence of Ritz's vectors
    TFltVV Q(N, Iters);
    double tmp = 1/sqrt((double)N);
    for (i = 0; i < N; i++)
        Q(i,0) = tmp;
    //converget Ritz's vectors
    TVec<TFltV> ConvgQV(Iters);
    TIntV CountConvgV(Iters);
    for (i = 0; i < Iters; i++) CountConvgV[i] = 0;
    // const int ConvgTreshold = 50;

    //diagonal and subdiagonal of T
    TFltV d(Iters+1), e(Iters+1);
    //eigenvectors of T
    //TFltVV V;
    TFltVV V(Iters, Iters);

    // z - current Lanczos's vector
    TFltV z(N), bb(Iters), aa(Iters), y(N);
    //printf("svd(%d,%d)...\n", NumEig, Iters);

    if (SvdMatrixProductP) {
        // A = Matrix'*Matrix
        MultiplyATA(Matrix, Q, 0, z);
    } else {
        // A = Matrix
        Matrix.Multiply(Q, 0, z);
    }

    for (int j = 0; j < (Iters-1); j++) {
        //printf("%d..\r",j+2);

        //calculates (j+1)-th Lanczos's vector
        // aa[j] = <Q(:,j), z>
        aa[j] = TLinAlg::DotProduct(Q, j, z);
        //printf(" %g -- ", aa[j].Val); //HACK

        TLinAlg::AddVec(-aa[j], Q, j, z);
        if (j > 0) {
            // z := -aa[j] * Q(:,j) + z
            TLinAlg::AddVec(-bb[j-1], Q, j-1, z);

            //reortogonalization
            if (ReOrtoType == ssotSelective || ReOrtoType == ssotFull) {
                for (i = 0; i <= j; i++) {
                    // if i-tj vector converget, than we have to ortogonalize against it
                    if ((ReOrtoType == ssotFull) ||
                        (bb[j-1] * TFlt::Abs(V(K-1, i)) < eps * t)) {

                        ConvgQV[i].Reserve(N,N); CountConvgV[i]++;
                        TFltV& vec = ConvgQV[i];
                        //vec = Q * V(:,i)
                        for (int k = 0; k < N; k++) {
                            vec[k] = 0.0;
                            for (int l = 0; l < K; l++)
                                vec[k] += Q(k,l) * V(l,i);
                        }
                        TLinAlg::AddVec(-TLinAlg::DotProduct(ConvgQV[i], z), ConvgQV[i], z ,z);
                    }
                }
            }
        }

        //adds (j+1)-th Lanczos's vector to Q
        bb[j] = TLinAlg::Norm(z);
    if (!(bb[j] > 1e-10)) {
      printf("Rank of matrix is only %d\n", j+2);
      printf("Last singular value is %g\n", bb[j].Val);
      break;
    }
        for (i = 0; i < N; i++)
            Q(i, j+1) = z[i] / bb[j];

        //next Lanzcos vector
        if (SvdMatrixProductP) {
            // A = Matrix'*Matrix
            MultiplyATA(Matrix, Q, j+1, z);
        } else {
            // A = Matrix
            Matrix.Multiply(Q, j+1, z);
        }

        //calculate T (K x K matrix)
        K = j + 2;
        // calculate diagonal
        for (i = 1; i < K; i++) d[i] = aa[i-1];
        d[K] = TLinAlg::DotProduct(Q, K-1, z);
        // calculate subdiagonal
        e[1] = 0.0;
        for (i = 2; i <= K; i++) e[i] = bb[i-2];

        //calculate 1-norm of T
        t = TFlt::GetMx(TFlt::Abs(d[1]) + TFlt::Abs(e[2]), TFlt::Abs(e[K]) + TFlt::Abs(d[K]));
        for (i = 2; i < K; i++)
            t = TFlt::GetMx(t, TFlt::Abs(e[i]) + TFlt::Abs(d[i]) + TFlt::Abs(e[i+1]));

        //set V to identity matrix
        //V.Gen(K,K);
        for (i = 0; i < K; i++) {
            for (int k = 0; k < K; k++)
                V(i,k) = 0.0;
            V(i,i) = 1.0;
        }

        //eigenvectors of T
        TNumericalStuff::EigSymmetricTridiag(d, e, K, V);
    }//for
    //printf("\n");

    // Finds NumEig largest eigen values
    TFltIntKdV sv(K);
    for (i = 0; i < K; i++) {
        sv[i].Key = TFlt::Abs(d[i+1]);
        sv[i].Dat = i;
    }
    sv.Sort(false);

    TFltV uu(Matrix.GetRows());
    const int FinalNumEig = TInt::GetMn(NumEig, K);
    EigValV.Reserve(FinalNumEig,0);
    EigVecVV.Gen(Matrix.GetCols(), FinalNumEig);
    for (i = 0; i < FinalNumEig; i++) {
        //printf("s[%d] = %20.15f\r", i, sv[i].Key.Val);
        int ii = sv[i].Dat;
        double sigma = d[ii+1].Val;
        // calculate singular value
        EigValV.Add(sigma);
        // calculate i-th right singular vector ( V := Q * W )
        TLinAlg::Multiply(Q, V, ii, EigVecVV, i);
    }
    //printf("done                           \n");
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSparseSVD::Lanczos2	(	const TMatrix &	Matrix,
		int	MaxNumEig,
		int	MaxSecs,
		const TSpSVDReOrtoType &	ReOrtoType,
		TFltV &	EigValV,
		TFltVV &	EigVecVV,
		const bool &	SvdMatrixProductP = `false`
	)		`[static]`

Definition at line 1272 of file linalg.cpp.

References TFlt::Abs(), TVec< TVal >::Add(), TLinAlg::AddVec(), TLinAlg::DotProduct(), TNumericalStuff::EigSymmetricTridiag(), TVVec< TVal >::Gen(), TMatrix::GetCols(), TFlt::GetMx(), TMatrix::GetRows(), TExeTm::GetSecs(), TExeTm::GetStr(), IAssert, TMatrix::Multiply(), TLinAlg::Multiply(), MultiplyATA(), TLinAlg::Norm(), TVec< TVal >::Reserve(), TVec< TVal >::Sort(), ssotFull, and ssotSelective.

Referenced by TSnap::GetInvParticipRat().

                                                                     {

  if (SvdMatrixProductP) {
    // if this fails, use transposed matrix
    IAssert(Matrix.GetRows() >= Matrix.GetCols());
  } else {
    IAssert(Matrix.GetRows() == Matrix.GetCols());
  }
  //IAssertR(NumEig <= Iters, TStr::Fmt("%d <= %d", NumEig, Iters));

  //if (ReOrtoType == ssotFull) printf("Full reortogonalization\n");
  int i, N = Matrix.GetCols(), K; // K - current dimension of T
  double t = 0.0, eps = 1e-6; // t - 1-norm of T

  //sequence of Ritz's vectors
  TFltVV Q(N, MaxNumEig);
  double tmp = 1/sqrt((double)N);
  for (i = 0; i < N; i++)
      Q(i,0) = tmp;
  //converget Ritz's vectors
  TVec<TFltV> ConvgQV(MaxNumEig);
  TIntV CountConvgV(MaxNumEig);
  for (i = 0; i < MaxNumEig; i++) CountConvgV[i] = 0;
  // const int ConvgTreshold = 50;

  //diagonal and subdiagonal of T
  TFltV d(MaxNumEig+1), e(MaxNumEig+1);
  //eigenvectors of T
  //TFltVV V;
  TFltVV V(MaxNumEig, MaxNumEig);

  // z - current Lanczos's vector
  TFltV z(N), bb(MaxNumEig), aa(MaxNumEig), y(N);
  //printf("svd(%d,%d)...\n", NumEig, Iters);

  if (SvdMatrixProductP) {
      // A = Matrix'*Matrix
      MultiplyATA(Matrix, Q, 0, z);
  } else {
      // A = Matrix
      Matrix.Multiply(Q, 0, z);
  }
  TExeTm ExeTm;
  for (int j = 0; j < (MaxNumEig-1); j++) {
    printf("%d [%s]..\r",j+2, ExeTm.GetStr());
    if (ExeTm.GetSecs() > MaxSecs) { break; }

    //calculates (j+1)-th Lanczos's vector
    // aa[j] = <Q(:,j), z>
    aa[j] = TLinAlg::DotProduct(Q, j, z);
    //printf(" %g -- ", aa[j].Val); //HACK

    TLinAlg::AddVec(-aa[j], Q, j, z);
    if (j > 0) {
        // z := -aa[j] * Q(:,j) + z
        TLinAlg::AddVec(-bb[j-1], Q, j-1, z);

        //reortogonalization
        if (ReOrtoType == ssotSelective || ReOrtoType == ssotFull) {
            for (i = 0; i <= j; i++) {
                // if i-tj vector converget, than we have to ortogonalize against it
                if ((ReOrtoType == ssotFull) ||
                    (bb[j-1] * TFlt::Abs(V(K-1, i)) < eps * t)) {

                    ConvgQV[i].Reserve(N,N); CountConvgV[i]++;
                    TFltV& vec = ConvgQV[i];
                    //vec = Q * V(:,i)
                    for (int k = 0; k < N; k++) {
                        vec[k] = 0.0;
                        for (int l = 0; l < K; l++)
                            vec[k] += Q(k,l) * V(l,i);
                    }
                    TLinAlg::AddVec(-TLinAlg::DotProduct(ConvgQV[i], z), ConvgQV[i], z ,z);
                }
            }
        }
    }

    //adds (j+1)-th Lanczos's vector to Q
    bb[j] = TLinAlg::Norm(z);
    if (!(bb[j] > 1e-10)) {
      printf("Rank of matrix is only %d\n", j+2);
      printf("Last singular value is %g\n", bb[j].Val);
      break;
    }
    for (i = 0; i < N; i++)
        Q(i, j+1) = z[i] / bb[j];

    //next Lanzcos vector
    if (SvdMatrixProductP) {
        // A = Matrix'*Matrix
        MultiplyATA(Matrix, Q, j+1, z);
    } else {
        // A = Matrix
        Matrix.Multiply(Q, j+1, z);
    }

    //calculate T (K x K matrix)
    K = j + 2;
    // calculate diagonal
    for (i = 1; i < K; i++) d[i] = aa[i-1];
    d[K] = TLinAlg::DotProduct(Q, K-1, z);
    // calculate subdiagonal
    e[1] = 0.0;
    for (i = 2; i <= K; i++) e[i] = bb[i-2];

    //calculate 1-norm of T
    t = TFlt::GetMx(TFlt::Abs(d[1]) + TFlt::Abs(e[2]), TFlt::Abs(e[K]) + TFlt::Abs(d[K]));
    for (i = 2; i < K; i++)
        t = TFlt::GetMx(t, TFlt::Abs(e[i]) + TFlt::Abs(d[i]) + TFlt::Abs(e[i+1]));

    //set V to identity matrix
    //V.Gen(K,K);
    for (i = 0; i < K; i++) {
        for (int k = 0; k < K; k++)
            V(i,k) = 0.0;
        V(i,i) = 1.0;
    }

    //eigenvectors of T
    TNumericalStuff::EigSymmetricTridiag(d, e, K, V);
  }//for
  printf("... calc %d.", K);
  // Finds NumEig largest eigen values
  TFltIntKdV sv(K);
  for (i = 0; i < K; i++) {
    sv[i].Key = TFlt::Abs(d[i+1]);
    sv[i].Dat = i;
  }
  sv.Sort(false);

  TFltV uu(Matrix.GetRows());
  const int FinalNumEig = K; //TInt::GetMn(NumEig, K);
  EigValV.Reserve(FinalNumEig,0);
  EigVecVV.Gen(Matrix.GetCols(), FinalNumEig);
  for (i = 0; i < FinalNumEig; i++) {
    //printf("s[%d] = %20.15f\r", i, sv[i].Key.Val);
    int ii = sv[i].Dat;
    double sigma = d[ii+1].Val;
    // calculate singular value
    EigValV.Add(sigma);
    // calculate i-th right singular vector ( V := Q * W )
    TLinAlg::Multiply(Q, V, ii, EigVecVV, i);
  }
  printf("  done\n");
}

Here is the call graph for this function:

Here is the caller graph for this function:

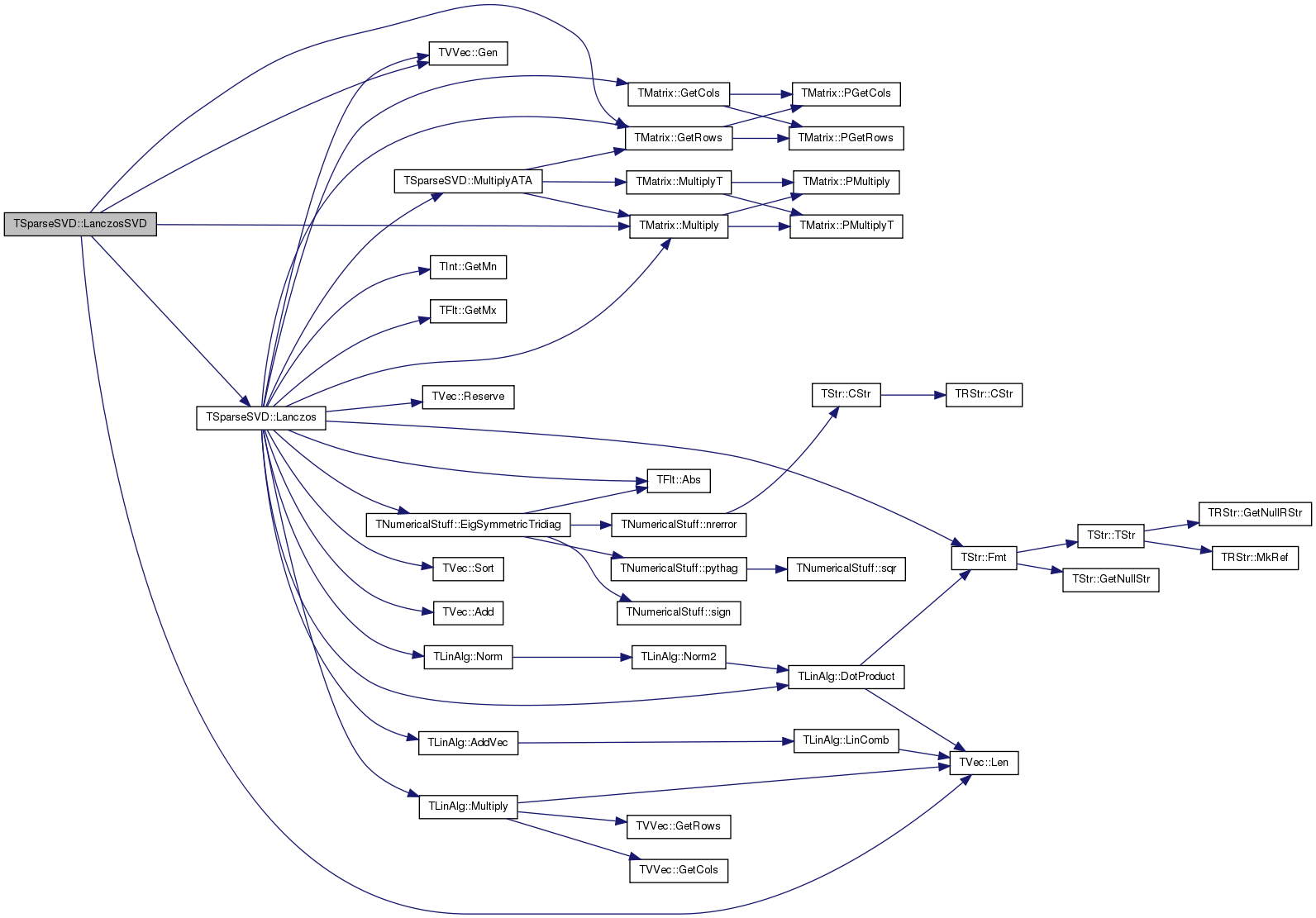
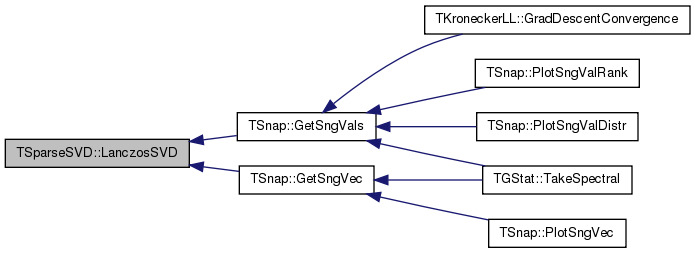
void TSparseSVD::LanczosSVD	(	const TMatrix &	Matrix,
		int	NumSV,
		int	Iters,
		const TSpSVDReOrtoType &	ReOrtoType,
		TFltV &	SgnValV,
		TFltVV &	LeftSgnVecVV,
		TFltVV &	RightSgnVecVV
	)		`[static]`

Definition at line 1436 of file linalg.cpp.

References TVVec< TVal >::Gen(), TMatrix::GetRows(), Lanczos(), TVec< TVal >::Len(), and TMatrix::Multiply().

Referenced by TSnap::GetSngVals(), and TSnap::GetSngVec().

                                                                     {

    // solve eigen problem for Matrix'*Matrix
    Lanczos(Matrix, NumSV, Iters, ReOrtoType, SgnValV, RightSgnVecVV, true);
    // calculate left singular vectors and sqrt singular values
    const int FinalNumSV = SgnValV.Len();
    LeftSgnVecVV.Gen(Matrix.GetRows(), FinalNumSV);
    TFltV LeftSgnVecV(Matrix.GetRows());
    for (int i = 0; i < FinalNumSV; i++) {
        if (SgnValV[i].Val < 0.0) { SgnValV[i] = 0.0; }
        const double SgnVal = sqrt(SgnValV[i]);
        SgnValV[i] = SgnVal;
        // calculate i-th left singular vector ( U := A * V * S^(-1) )
        Matrix.Multiply(RightSgnVecVV, i, LeftSgnVecV);
        for (int j = 0; j < LeftSgnVecV.Len(); j++) {
            LeftSgnVecVV(j,i) = LeftSgnVecV[j] / SgnVal; }
    }
    //printf("done                           \n");
}

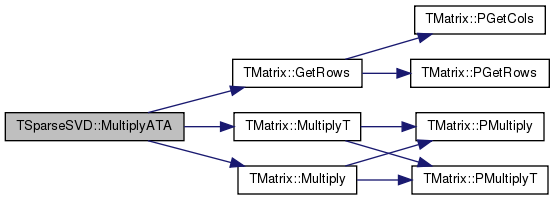
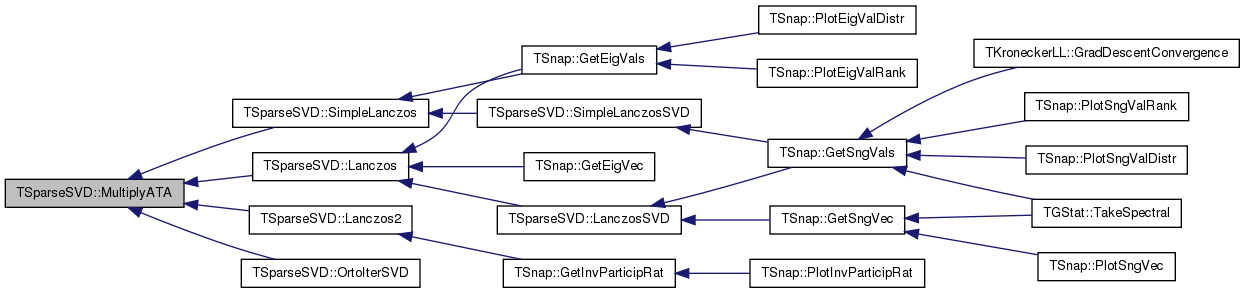
Here is the call graph for this function:

Here is the caller graph for this function:

void TSparseSVD::MultiplyATA	(	const TMatrix &	Matrix,
		const TFltVV &	Vec,
		int	ColId,
		TFltV &	Result
	)		`[static, private]`

Definition at line 992 of file linalg.cpp.

References TMatrix::GetRows(), TMatrix::Multiply(), and TMatrix::MultiplyT().

Referenced by Lanczos(), Lanczos2(), OrtoIterSVD(), and SimpleLanczos().

                                                     {
    TFltV tmp(Matrix.GetRows());
    // tmp = A * Vec(:,ColId)
    Matrix.Multiply(Vec, ColId, tmp);
    // Vec = A' * tmp
    Matrix.MultiplyT(tmp, Result);
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSparseSVD::MultiplyATA	(	const TMatrix &	Matrix,
		const TFltV &	Vec,
		TFltV &	Result
	)		`[static, private]`

Definition at line 1001 of file linalg.cpp.

References TMatrix::GetRows(), TMatrix::Multiply(), and TMatrix::MultiplyT().

                                         {
    TFltV tmp(Matrix.GetRows());
    // tmp = A * Vec
    Matrix.Multiply(Vec, tmp);
    // Vec = A' * tmp
    Matrix.MultiplyT(tmp, Result);
}

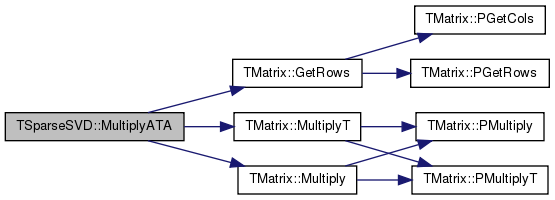
Here is the call graph for this function:

void TSparseSVD::OrtoIterSVD	(	const TMatrix &	Matrix,
		int	NumSV,
		int	IterN,
		TFltV &	SgnValV
	)		`[static]`

Definition at line 1010 of file linalg.cpp.

References TVec< TVal >::Add(), TMatrix::GetCols(), TRnd::GetUniDev(), TLinAlg::GS(), MultiplyATA(), TLinAlg::Norm(), and TVec< TVal >::Reserve().

                                              {

    int i, j, k;
    int N = Matrix.GetCols(), M = NumSV;
    TFltVV Q(N, M);

    // Q = rand(N,M)
    TRnd rnd;
    for (i = 0; i < N; i++) {
        for (j = 0; j < M; j++)
            Q(i,j) = rnd.GetUniDev();
    }

    TFltV tmp(N);
    for (int IterC = 0; IterC < IterN; IterC++) {
        printf("%d..", IterC);
        // Gram-Schmidt
        TLinAlg::GS(Q);
        // Q = A'*A*Q
        for (int ColId = 0; ColId < M; ColId++) {
            MultiplyATA(Matrix, Q, ColId, tmp);
            for (k = 0; k < N; k++) Q(k,ColId) = tmp[k];
        }
    }

    SgnValV.Reserve(NumSV,0);
    for (i = 0; i < NumSV; i++)
        SgnValV.Add(sqrt(TLinAlg::Norm(Q,i)));
    TLinAlg::GS(Q);
}

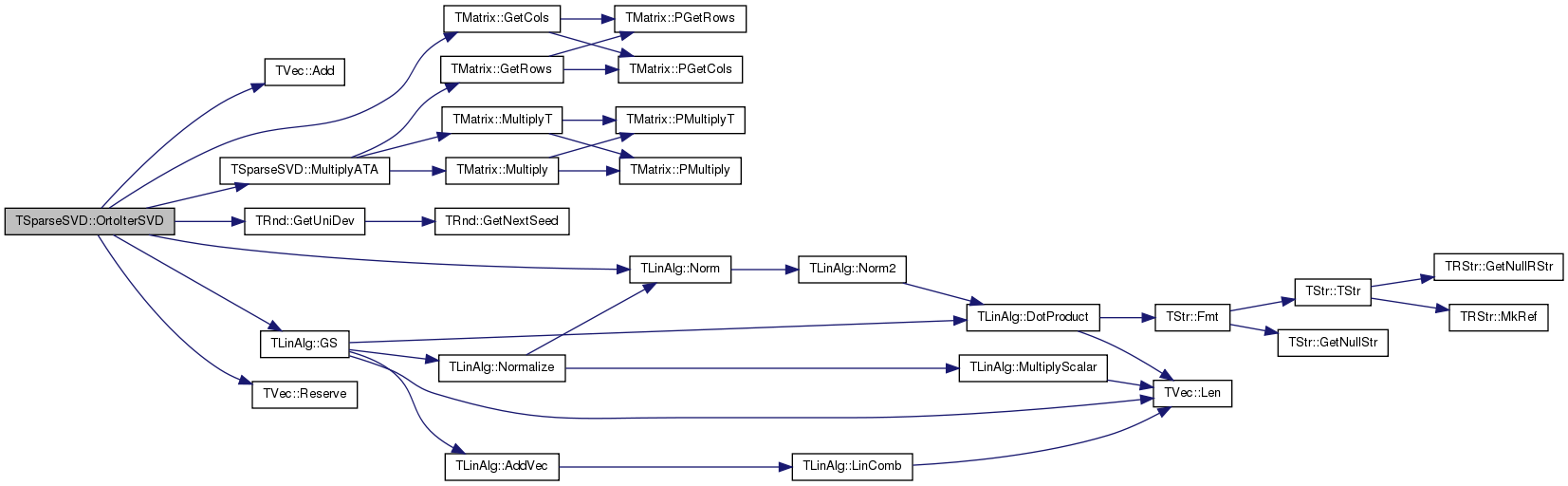
Here is the call graph for this function:

void TSparseSVD::Project	(	const TIntFltKdV &	Vec,
		const TFltVV &	U,
		TFltV &	ProjVec
	)		`[static]`

Definition at line 1458 of file linalg.cpp.

References TVec< TVal >::Add(), TVec< TVal >::Gen(), TVVec< TVal >::GetCols(), and TVec< TVal >::Len().

                                                                               {
    const int m = U.GetCols(); // number of columns

    ProjVec.Gen(m, 0);
    for (int j = 0; j < m; j++) {
        double x = 0.0;
        for (int i = 0; i < Vec.Len(); i++)
            x += U(Vec[i].Key, j) * Vec[i].Dat;
        ProjVec.Add(x);
    }
}

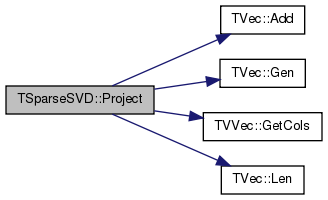
Here is the call graph for this function:

void TSparseSVD::SimpleLanczos	(	const TMatrix &	Matrix,
		const int &	NumEig,
		TFltV &	EigValV,
		const bool &	DoLocalReortoP = `false`,
		const bool &	SvdMatrixProductP = `false`
	)		`[static]`

Definition at line 1042 of file linalg.cpp.

References TFlt::Abs(), TVec< TVal >::Add(), TLinAlg::AddVec(), TLinAlg::DotProduct(), TNumericalStuff::EigSymmetricTridiag(), TLAMisc::FillIdentity(), TVec< TVal >::Gen(), TMatrix::GetCols(), TMatrix::GetRows(), IAssert, TVec< TVal >::Last(), TVec< TVal >::Len(), TMatrix::Multiply(), MultiplyATA(), TLinAlg::MultiplyScalar(), TLinAlg::Norm(), and TVec< TVal >::Sort().

Referenced by TSnap::GetEigVals(), and SimpleLanczosSVD().

                                                                   {

    if (SvdMatrixProductP) {
        // if this fails, use transposed matrix
        IAssert(Matrix.GetRows() >= Matrix.GetCols());
    } else {
        IAssert(Matrix.GetRows() == Matrix.GetCols());
    }

    const int N = Matrix.GetCols(); // size of matrix
    TFltV r(N), v0(N), v1(N); // current vector and 2 previous ones
    TFltV alpha(NumEig, 0), beta(NumEig, 0); // diagonal and subdiagonal of T

    printf("Calculating %d eigen-values of %d x %d matrix\n", NumEig, N, N);

    // set starting vector
    //TRnd Rnd(0);
    for (int i = 0; i < N; i++) {
        r[i] = 1/sqrt((double)N); // Rnd.GetNrmDev();
        v0[i] = v1[i] = 0.0;
    }
    beta.Add(TLinAlg::Norm(r));

    for (int j = 0; j < NumEig; j++) {
        printf("%d\r", j+1);
        // v_j -> v_(j-1)
        v0 = v1;
        // v_j = (1/beta_(j-1)) * r
        TLinAlg::MultiplyScalar(1/beta[j], r, v1);
        // r = A*v_j
        if (SvdMatrixProductP) {
            // A = Matrix'*Matrix
            MultiplyATA(Matrix, v1, r);
        } else {
            // A = Matrix
            Matrix.Multiply(v1, r);
        }
        // r = r - beta_(j-1) * v_(j-1)
        TLinAlg::AddVec(-beta[j], v0, r, r);
        // alpha_j = vj'*r
        alpha.Add(TLinAlg::DotProduct(v1, r));
        // r = r - v_j * alpha_j
        TLinAlg::AddVec(-alpha[j], v1, r, r);
        // reortogonalization if neessary
        if (DoLocalReortoP) { } //TODO
        // beta_j = ||r||_2
        beta.Add(TLinAlg::Norm(r));
        // compoute approximatie eigenvalues T_j
        // test bounds for convergence
    }
    printf("\n");

    // prepare matrix T
    TFltV d(NumEig + 1), e(NumEig + 1);
    d[1] = alpha[0]; d[0] = e[0] = e[1] = 0.0;
    for (int i = 1; i < NumEig; i++) {
        d[i+1] = alpha[i]; e[i+1] = beta[i]; }
    // solve eigne problem for tridiagonal matrix with diag d and subdiag e
    TFltVV S(NumEig+1,NumEig+1); // eigen-vectors
    TLAMisc::FillIdentity(S); // make it identity
    TNumericalStuff::EigSymmetricTridiag(d, e, NumEig, S); // solve
    //TLAMisc::PrintTFltV(d, "AllEigV");

    // check convergence
    TFltKdV AllEigValV(NumEig, 0);
    for (int i = 1; i <= NumEig; i++) {
        const double ResidualNorm = TFlt::Abs(S(i-1, NumEig-1) * beta.Last());
        if (ResidualNorm < 1e-5)
            AllEigValV.Add(TFltKd(TFlt::Abs(d[i]), d[i]));
    }

    // prepare results
    AllEigValV.Sort(false); EigValV.Gen(NumEig, 0);
    for (int i = 0; i < AllEigValV.Len(); i++) {
        if (i == 0 || (TFlt::Abs(AllEigValV[i].Dat/AllEigValV[i-1].Dat) < 0.9999))
            EigValV.Add(AllEigValV[i].Dat);
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

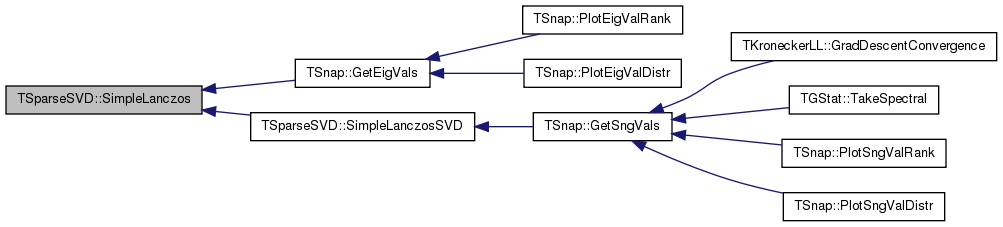
void TSparseSVD::SimpleLanczosSVD	(	const TMatrix &	Matrix,
		const int &	CalcSV,
		TFltV &	SngValV,
		const bool &	DoLocalReortoP = `false`
	)		`[static]`

Definition at line 1422 of file linalg.cpp.

References TVec< TVal >::Len(), and SimpleLanczos().

Referenced by TSnap::GetSngVals().

                                                                      {

    SimpleLanczos(Matrix, CalcSV, SngValV, DoLocalReorto, true);
    for (int SngValN = 0; SngValN < SngValV.Len(); SngValN++) {
      //IAssert(SngValV[SngValN] >= 0.0);
      if (SngValV[SngValN] < 0.0) {
        printf("bad sng val: %d %g\n", SngValN, SngValV[SngValN]());
        SngValV[SngValN] = 0;
      }
      SngValV[SngValN] = sqrt(SngValV[SngValN].Val);
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

The documentation for this class was generated from the following files:

glib-core/linalg.h
glib-core/linalg.cpp

Static Public Member Functions

Static Private Member Functions

Detailed Description

Member Function Documentation