TSnap Namespace Reference

Main namespace for all the Snap global entities. More...

Namespaces
	TSnapDetail

Classes
struct	IsBipart
	Tests (at compile time) if the graph is a bipartite graph type. More...
struct	IsBipart< TBPGraph >
struct	IsDirected
	Tests (at compile time) if the graph is directed. More...
struct	IsDirected< TBigNet< TNodeData, IsDir > >
struct	IsDirected< TBigNet< TNodeData, true > >
struct	IsDirected< TNEANet >
struct	IsDirected< TNEGraph >
struct	IsDirected< TNGraph >
struct	IsDirected< TNodeEDatNet< TNodeData, TEdgeData > >
struct	IsDirected< TNodeEdgeNet< TNodeData, TEdgeData > >
struct	IsDirected< TNodeNet< TNodeData > >
struct	IsDirected< TTimeNENet >
struct	IsDirected< TTimeNet >
struct	IsEdgeDat
	Tests (at compile time) if the graph is a network with data on edges. More...
struct	IsEdgeDat< TNodeEDatNet< TNodeData, TEdgeData > >
struct	IsEdgeDat< TNodeEdgeNet< TNodeData, TEdgeData > >
struct	IsEdgeDat< TTimeNENet >
struct	IsMultiGraph
	Tests (at compile time) if the graph is a multigraph with multiple edges between the same nodes. More...
struct	IsMultiGraph< TNEANet >
struct	IsMultiGraph< TNEGraph >
struct	IsMultiGraph< TNodeEdgeNet< TNodeData, TEdgeData > >
struct	IsMultiGraph< TTimeNENet >
struct	IsNodeDat
	Tests (at compile time) if the graph is a network with data on nodes. More...
struct	IsNodeDat< TBigNet< TNodeData, IsDir > >
struct	IsNodeDat< TNodeEDatNet< TNodeData, TEdgeData > >
struct	IsNodeDat< TNodeEdgeNet< TNodeData, TEdgeData > >
struct	IsNodeDat< TNodeNet< TNodeData > >
struct	IsNodeDat< TTimeNENet >
struct	IsNodeDat< TTimeNet >
struct	IsSources
	Tests (at compile time) if the nodes store only out-edges, but not in-edges. More...
class	TPRManager
	Push relabel attr manager. More...

Functions
template<class PGraph >
int	CntInDegNodes (const PGraph &Graph, const int &NodeInDeg)
	Returns the number of nodes with in-degree NodeInDeg. More...
template<class PGraph >
int	CntOutDegNodes (const PGraph &Graph, const int &NodeOutDeg)
	Returns the number of nodes with out-degree NodeOutDeg. More...
template<class PGraph >
int	CntDegNodes (const PGraph &Graph, const int &NodeDeg)
	Returns the number of nodes with degree NodeDeg. More...
template<class PGraph >
int	CntNonZNodes (const PGraph &Graph)
	Returns the number of nodes with degree greater than 0. More...
template<class PGraph >
int	CntEdgesToSet (const PGraph &Graph, const int &NId, const TIntSet &NodeSet)
	Returns the number of nodes in NodeSet that have an edge to the node NId. More...
template<class PGraph >
int	GetMxDegNId (const PGraph &Graph)
	Returns a randomly chosen node from all the nodes with the maximum degree. More...
template<class PGraph >
int	GetMxInDegNId (const PGraph &Graph)
	Returns a randomly chosen node from all the nodes with the maximum in-degree. More...
template<class PGraph >
int	GetMxOutDegNId (const PGraph &Graph)
	Returns a randomly chosen node from all the nodes with the maximum out-degree. More...
template<class PGraph >
void	GetInDegCnt (const PGraph &Graph, TIntPrV &DegToCntV)
	Returns an in-degree histogram: a set of pairs (in-degree, number of nodes of such in-degree) More...
template<class PGraph >
void	GetInDegCnt (const PGraph &Graph, TFltPrV &DegToCntV)
	Returns an in-degree histogram: a set of pairs (in-degree, number of nodes of such in-degree) More...
template<class PGraph >
void	GetOutDegCnt (const PGraph &Graph, TIntPrV &DegToCntV)
	Returns an out-degree histogram: a set of pairs (out-degree, number of nodes of such out-degree) More...
template<class PGraph >
void	GetOutDegCnt (const PGraph &Graph, TFltPrV &DegToCntV)
	Returns an out-degree histogram: a set of pairs (out-degree, number of nodes of such out-degree) More...
template<class PGraph >
void	GetDegCnt (const PGraph &Graph, TIntPrV &DegToCntV)
	Returns a degree histogram: a set of pairs (degree, number of nodes of such degree) More...
template<class PGraph >
void	GetDegCnt (const PGraph &Graph, TFltPrV &DegToCntV)
	Returns a degree histogram: a set of pairs (degree, number of nodes of such degree) More...
template<class PGraph >
void	GetDegSeqV (const PGraph &Graph, TIntV &DegV)
	Returns a degree sequence vector. More...
template<class PGraph >
void	GetDegSeqV (const PGraph &Graph, TIntV &InDegV, TIntV &OutDegV)
	Returns an in- and out-degree sequence vectors. More...
template<class PGraph >
void	GetNodeInDegV (const PGraph &Graph, TIntPrV &NIdInDegV)
	Returns a vector of pairs (node id, node in-degree) More...
template<class PGraph >
void	GetNodeOutDegV (const PGraph &Graph, TIntPrV &NIdOutDegV)
	Returns a vector of pairs (node id, node out-degree) More...
template<class PGraph >
int	CntUniqUndirEdges (const PGraph &Graph)
	Counts unique undirected edges in the graph Graph. Nodes (u,v)<. More...
template<class PGraph >
int	CntUniqDirEdges (const PGraph &Graph)
	Counts unique directed edges in the graph Graph. Nodes (u,v)<. More...
template<class PGraph >
int	CntUniqBiDirEdges (const PGraph &Graph)
	Counts unique bidirectional edges in the graph Graph. Edge is bidirectional is there exist directed edges in both directions: (u,v) and (v,u) More...
template<class PGraph >
int	CntSelfEdges (const PGraph &Graph)
	Counts the number fo of self-edges in a graph. Edge (u,u) is a self-edge. More...
template<class PGraph >
PGraph	GetUnDir (const PGraph &Graph)
	Returs an undirected version of the graph. For every edge (u,v) an edge (v,u) is added (if it does not yet exist). More...
template<class PGraph >
void	MakeUnDir (const PGraph &Graph)
	Makes the graph undirected. For every edge (u,v) an edge (v,u) is added (if it does not yet exist). More...
template<class PGraph >
void	AddSelfEdges (const PGraph &Graph)
	Adds a self-edge to every node in the graph. More...
template<class PGraph >
void	DelSelfEdges (const PGraph &Graph)
	Removes all the self-edges from the graph. More...
template<class PGraph >
void	DelNodes (PGraph &Graph, const TIntV &NIdV)
	Removes nodes with ids stored in NIdV from the graph. More...
template<class PGraph >
void	DelZeroDegNodes (PGraph &Graph)
	Removes all the zero-degree nodes, that isolated nodes, from the graph. More...
template<class PGraph >
void	DelDegKNodes (PGraph &Graph, const int &OutDegK, const int &InDegK)
	Removes all the node of out-degree OutDegK and all the nodes of in-degree InDegK from the graph. More...
template<class PGraph >
bool	IsTree (const PGraph &Graph, int &RootNIdX)
template<class PGraph >
int	GetTreeRootNId (const PGraph &Graph)
template<class PGraph >
void	GetTreeSig (const PGraph &Graph, const int &RootNId, TIntV &Sig)
template<class PGraph >
void	GetTreeSig (const PGraph &Graph, const int &RootNId, TIntV &Sig, TIntPrV &NodeMap)
template<class PGraph >
void	GetAnf (const PGraph &Graph, const int &SrcNId, TIntFltKdV &DistNbrsV, const int &MxDist, const bool &IsDir, const int &NApprox=32)
template<class PGraph >
void	GetAnf (const PGraph &Graph, TIntFltKdV &DistNbrsV, const int &MxDist, const bool &IsDir, const int &NApprox=32)
template<class PGraph >
double	GetAnfEffDiam (const PGraph &Graph, const bool &IsDir, const double &Percentile, const int &NApprox)
template<class PGraph >
double	GetAnfEffDiam (const PGraph &Graph, const int NRuns=1, int NApprox=-1)
template<class PGraph >
void	TestAnf ()
template<class PGraph >
PNGraph	GetBfsTree (const PGraph &Graph, const int &StartNId, const bool &FollowOut, const bool &FollowIn)
	Returns a directed Breadth-First-Search tree rooted at StartNId. More...
template<class PGraph >
int	GetSubTreeSz (const PGraph &Graph, const int &StartNId, const bool &FollowOut, const bool &FollowIn, int &TreeSzX, int &TreeDepthX)
	Returns the BFS tree size (number of nodes) and depth (number of levels) by following in-links (parameter FollowIn = true) and/or out-links (parameter FollowOut = true) of node StartNId. More...
template<class PGraph >
int	GetNodesAtHop (const PGraph &Graph, const int &StartNId, const int &Hop, TIntV &NIdV, const bool &IsDir=false)
	Finds IDs of all nodes that are at distance Hop from node StartNId. More...
template<class PGraph >
int	GetNodesAtHops (const PGraph &Graph, const int &StartNId, TIntPrV &HopCntV, const bool &IsDir=false)
	Returns the number of nodes at each hop distance from the starting node StartNId. More...
template<class PGraph >
int	GetShortPath (const PGraph &Graph, const int &SrcNId, const int &DstNId, const bool &IsDir=false)
	Returns the length of the shortest path from node SrcNId to node DstNId. More...
template<class PGraph >
int	GetShortPath (const PGraph &Graph, const int &SrcNId, TIntH &NIdToDistH, const bool &IsDir=false, const int &MaxDist=TInt::Mx)
	Returns the length of the shortest path from node SrcNId to all other nodes in the network. More...
template<class PGraph >
int	GetBfsFullDiam (const PGraph &Graph, const int &NTestNodes, const bool &IsDir=false)
	Returns the (approximation of the) Diameter (maximum shortest path length) of a graph (by performing BFS from NTestNodes random starting nodes). More...
template<class PGraph >
double	GetBfsEffDiam (const PGraph &Graph, const int &NTestNodes, const bool &IsDir=false)
	Returns the (approximation of the) Effective Diameter (90-th percentile of the distribution of shortest path lengths) of a graph (by performing BFS from NTestNodes random starting nodes). More...
template<class PGraph >
double	GetBfsEffDiam (const PGraph &Graph, const int &NTestNodes, const bool &IsDir, double &EffDiamX, int &FullDiamX)
	Returns the (approximation of the) Effective Diameter and the Diameter of a graph (by performing BFS from NTestNodes random starting nodes). More...
template<class PGraph >
double	GetBfsEffDiam (const PGraph &Graph, const int &NTestNodes, const bool &IsDir, double &EffDiamX, int &FullDiamX, double &AvgSPLX)
	Returns the (approximation of the) Effective Diameter, the Diameter and the Average Shortest Path length in a graph (by performing BFS from NTestNodes random starting nodes). GetBfsEffDiam3. More...
template<class PGraph >
double	GetBfsEffDiam (const PGraph &Graph, const int &NTestNodes, const TIntV &SubGraphNIdV, const bool &IsDir, double &EffDiamX, int &FullDiamX)
	Use the whole graph (all edges) to measure the shortest path lengths but only report the path lengths between nodes in the SubGraphNIdV. GetBfsEffDiam4. More...
double	GetDegreeCentr (const PUNGraph &Graph, const int &NId)
double	GetFarnessCentr (const PUNGraph &Graph, const int &NId)
double	GetClosenessCentr (const PUNGraph &Graph, const int &NId)
void	GetBetweennessCentr (const PUNGraph &Graph, const TIntV &BtwNIdV, TIntFltH &NodeBtwH, const bool &DoNodeCent, TIntPrFltH &EdgeBtwH, const bool &DoEdgeCent)
void	GetBetweennessCentr (const PUNGraph &Graph, TIntFltH &NodeBtwH, const double &NodeFrac)
void	GetBetweennessCentr (const PUNGraph &Graph, TIntPrFltH &EdgeBtwH, const double &NodeFrac)
void	GetBetweennessCentr (const PUNGraph &Graph, TIntFltH &NodeBtwH, TIntPrFltH &EdgeBtwH, const double &NodeFrac)
void	GetEigenVectorCentr (const PUNGraph &Graph, TIntFltH &NIdEigenH, const double &Eps, const int &MaxIter)
template<class PGraph >
int	GetNodeEcc (const PGraph &Graph, const int &NId, const bool &IsDir=false)
template<class PGraph >
void	GetPageRank (const PGraph &Graph, TIntFltH &PRankH, const double &C=0.85, const double &Eps=1e-4, const int &MaxIter=100)
template<class PGraph >
void	GetHits (const PGraph &Graph, TIntFltH &NIdHubH, TIntFltH &NIdAuthH, const int &MaxIter=20)
double	CommunityGirvanNewman (PUNGraph &Graph, TCnComV &CmtyV)
double	Infomap (PUNGraph &Graph, TCnComV &CmtyV)
double	CommunityCNM (const PUNGraph &Graph, TCnComV &CmtyV)
template<typename PGraph >
double	GetModularity (const PGraph &G, const TIntV &NIdV, int GEdges=-1)
template<typename PGraph >
double	GetModularity (const PGraph &G, const TCnComV &CmtyV, int GEdges=-1)
template<typename PGraph >
void	GetEdgesInOut (const PGraph &Graph, const TIntV &NIdV, int &EdgesInX, int &EdgesOutX)
void	GetBiConSzCnt (const PUNGraph &Graph, TIntPrV &SzCntV)
	Returns a distribution of bi-connected component sizes. More...
void	GetBiCon (const PUNGraph &Graph, TCnComV &BiCnComV)
	Returns all bi-connected components of a Graph. More...
void	GetArtPoints (const PUNGraph &Graph, TIntV &ArtNIdV)
	Returns articulation points of a Graph. More...
void	GetEdgeBridges (const PUNGraph &Graph, TIntPrV &EdgeV)
	Returns bridge edges of a Graph. More...
void	Get1CnComSzCnt (const PUNGraph &Graph, TIntPrV &SzCntV)
	Distribution of sizes of 1-components, maximal number of components that can be disconnected from the Graph by removing a single edge. More...
void	Get1CnCom (const PUNGraph &Graph, TCnComV &Cn1ComV)
	Returns 1-components: maximal connected components of that can be disconnected from the Graph by removing a single edge. More...
PUNGraph	GetMxBiCon (const PUNGraph &Graph, const bool &RenumberNodes=false)
	Returns a graph representing the largest bi-connected component on an undirected Graph. More...
template<class PGraph >
void	GetNodeWcc (const PGraph &Graph, const int &NId, TIntV &CnCom)
	Returns (via output parameter CnCom) all nodes that are in the same connected component as node NId. More...
template<class PGraph >
bool	IsConnected (const PGraph &Graph)
	Tests whether the Graph is (weakly) connected. More...
template<class PGraph >
bool	IsWeaklyConn (const PGraph &Graph)
	Tests whether the Graph is weakly connected. More...
template<class PGraph >
void	GetWccSzCnt (const PGraph &Graph, TIntPrV &WccSzCnt)
	Returns a distribution of weakly connected component sizes. More...
template<class PGraph >
void	GetWccs (const PGraph &Graph, TCnComV &CnComV)
	Returns all weakly connected components in a Graph. More...
template<class PGraph >
void	GetSccSzCnt (const PGraph &Graph, TIntPrV &SccSzCnt)
	Returns a distribution of strongly connected component sizes. More...
template<class PGraph >
void	GetSccs (const PGraph &Graph, TCnComV &CnComV)
	Returns all strongly connected components in a Graph. More...
template<class PGraph >
double	GetMxWccSz (const PGraph &Graph)
	Returns the fraction of nodes in the largest weakly connected component of a Graph. More...
template<class PGraph >
double	GetMxSccSz (const PGraph &Graph)
	Returns the fraction of nodes in the largest strongly connected component of a Graph. More...
template<class PGraph >
PGraph	GetMxWcc (const PGraph &Graph)
	Returns a graph representing the largest weakly connected component on an input Graph. More...
template<class PGraph >
PGraph	GetMxScc (const PGraph &Graph)
	Returns a graph representing the largest strongly connected component on an input Graph. More...
template<class PGraph >
PGraph	GetMxBiCon (const PGraph &Graph)
	Returns a graph representing the largest bi-connected component on an input Graph. More...
int	IntFlowBiDBFS (const PNEANet &Net, const int &CapIndex, TIntV &Flow, TIntQ &FwdNodeQ, TIntH &PredEdgeH, TIntQ &BwdNodeQ, TIntH &SuccEdgeH, const int &SrcNId, const int &SnkNId)
int	FindAugV (const PNEANet &Net, const int &CapIndex, TIntV &Flow, TIntQ &FwdNodeQ, TIntH &PredEdgeH, TIntQ &BwdNodeQ, TIntH &SuccEdgeH, TIntV &MidToSrcAugV, TIntV &MidToSnkAugV, const int &SrcNId, const int &SnkNId)
	Returns the amount the flow can be augmented over the paths, 0 if no path can be found. More...
int	GetMaxFlowIntEK (PNEANet &Net, const int &SrcNId, const int &SnkNId)
	Returns the maximum integer valued flow in the network Net from source SrcNId to sink SnkNId. More...
void	PushToOutNbr (TPRManager &PRM, const int &NId, const int &OutNId, const int &EId)
	Pushes flow from a node NId to a neighbor OutNId over edge EId. More...
void	PushToInNbr (TPRManager &PRM, const int &NId, const int &InNId, const int &EId)
	Returns flow from a node NId to a neighbor InNId over edge EId. More...
void	Relabel (TPRManager &PRM, const int &NId, const TNEANet::TNodeI &NI)
	Increases the label of a node NId to allow valid pushes to some neighbor. More...
int	PushRelabel (TPRManager &PRM, const int &NId, const TNEANet::TNodeI &NI)
	Returns the ID of the neighbor that NId pushes to, -1 if no push was made. More...
void	GlobalRelabel (PNEANet &Net, TPRManager &PRM, const int &SrcNId, const int &SnkNId)
	Implements the Global Relabeling heuristic. More...
int	GetMaxFlowIntPR (PNEANet &Net, const int &SrcNId, const int &SnkNId)
	Returns the maximum integer valued flow in the network Net from source SrcNId to sink SnkNId. More...
const TStr	CapAttrName ("capacity")
TStr	GetFlagStr (const TGraphFlag &GraphFlag)
	Returns a string representation of a flag. More...
template<class PGraph >
void	PrintInfo (const PGraph &Graph, const TStr &Desc="", const TStr &OutFNm="", const bool &Fast=true)
	Prints basic graph statistics. More...
template<class PGraph >
int64	GetTriads (const PGraph &Graph, int64 &ClosedTriadsX, int64 &OpenTriadsX, int SampleNodes)
	Computes the number of Closed and Open triads. More...
template<class PGraph >
int	GetKCoreNodes (const PGraph &Graph, TIntPrV &CoreIdSzV)
	Returns the number of nodes in each core of order K (where K=0, 1, ...) More...
template<class PGraph >
int	GetKCoreEdges (const PGraph &Graph, TIntPrV &CoreIdSzV)
	Returns the number of edges in each core of order K (where K=0, 1, ...) More...
PBPGraph	GenRndBipart (const int &LeftNodes, const int &RightNodes, const int &Edges, TRnd &Rnd=TInt::Rnd)
	Generates a random bipartite graph. More...
PUNGraph	GenRndDegK (const int &Nodes, const int &NodeDeg, const int &NSwitch=100, TRnd &Rnd=TInt::Rnd)
	Generates a random graph where each node has degree exactly NodeDeg. More...
PUNGraph	GenRndPowerLaw (const int &Nodes, const double &PowerExp, const bool &ConfModel=true, TRnd &Rnd=TInt::Rnd)
	Generates a random scale-free graph with power-law degree distribution. More...
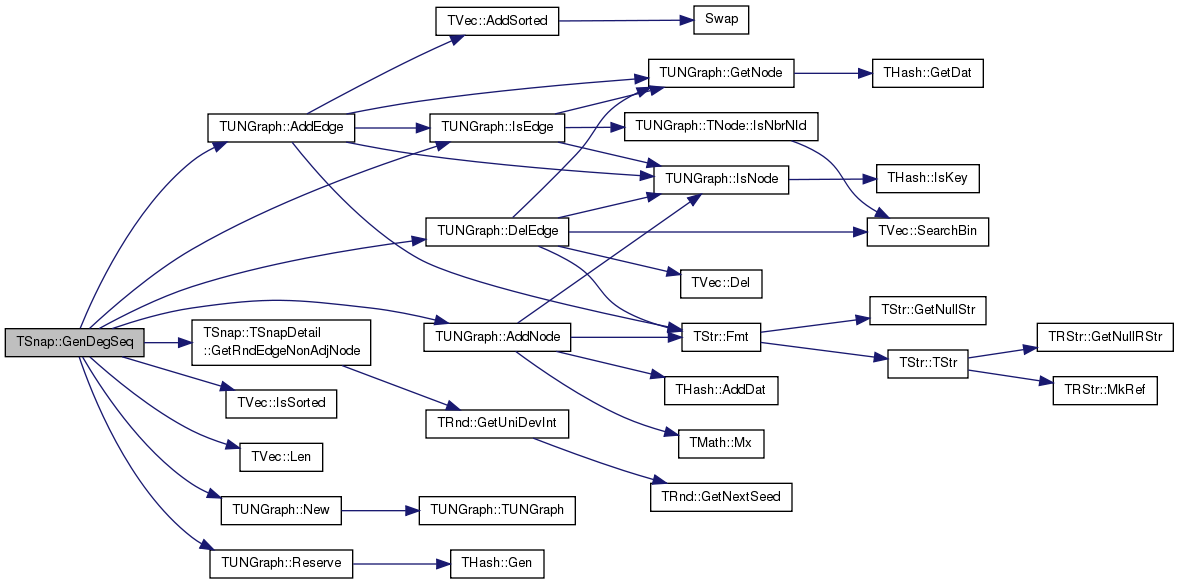
PUNGraph	GenDegSeq (const TIntV &DegSeqV, TRnd &Rnd=TInt::Rnd)
	Generates a random graph with exact degree sequence. More...
PUNGraph	GenConfModel (const TIntV &DegSeqV, TRnd &Rnd=TInt::Rnd)
	Generates a random undirect graph with a given degree sequence. More...
PUNGraph	GenRewire (const PUNGraph &Graph, const int &NSwitch=100, TRnd &Rnd=TInt::Rnd)
	Rewire a random undirected graph. Keeps node degrees the same, but randomly rewires the edges. More...
PNGraph	GenRewire (const PNGraph &Graph, const int &NSwitch=100, TRnd &Rnd=TInt::Rnd)
	Rewire a random directed graph. Keeps node degrees the same, but randomly rewires the edges. More...
PBPGraph	GenRewire (const PBPGraph &Graph, const int &NSwitch=100, TRnd &Rnd=TInt::Rnd)
	Rewire a random bipartite graph. Keeps node degrees the same, but randomly rewires the edges. More...
PUNGraph	GenPrefAttach (const int &Nodes, const int &NodeOutDeg, TRnd &Rnd=TInt::Rnd)
	Generates a power-law degree distribution using Barabasi-Albert model of scale-free graphs. More...
PUNGraph	GenConfModel (const PUNGraph &G)
	Generate a random graph using (approximately) the same node degrees as in G using the configuration model. More...
PUNGraph	GenGeoPrefAttach (const int &Nodes, const int &OutDeg, const double &Beta, TRnd &Rnd=TInt::Rnd)
	Generates a random scale-free graph using the Geometric Preferential model. More...
PUNGraph	GenSmallWorld (const int &Nodes, const int &NodeOutDeg, const double &RewireProb, TRnd &Rnd=TInt::Rnd)
	Generates a randomly small-world graph using the Watts-Strogatz model. More...
PNGraph	GenForestFire (const int &Nodes, const double &FwdProb, const double &BckProb)
	Generates a random Forest Fire, directed graph with given probabilities. More...
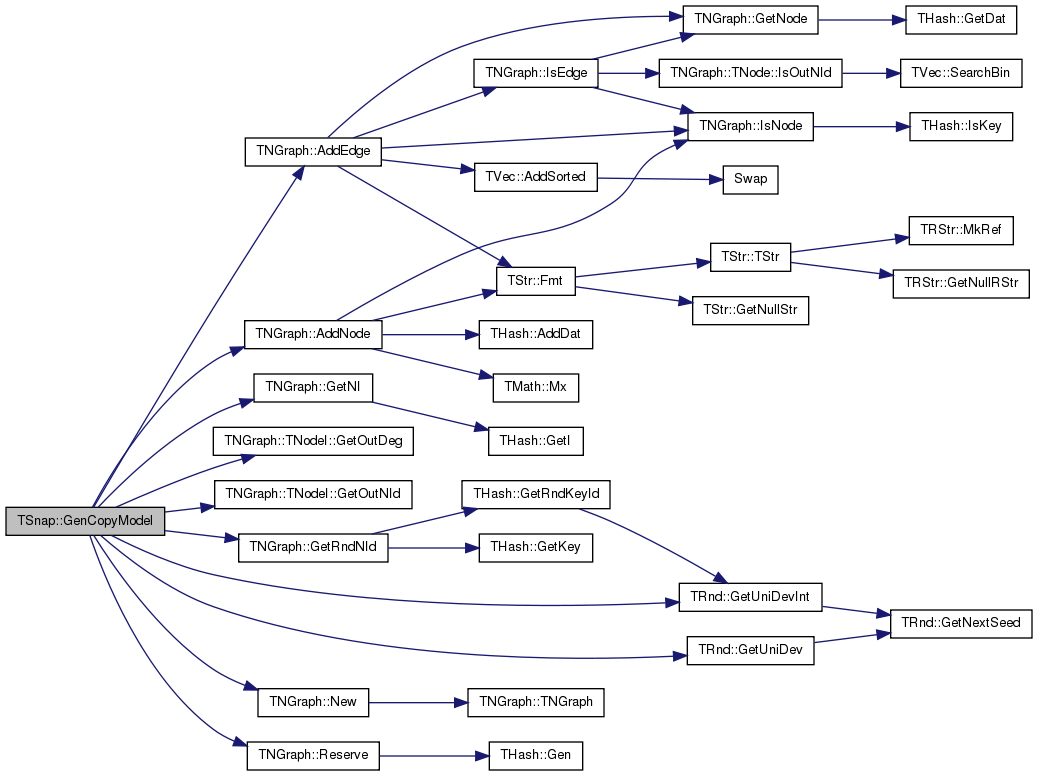
PNGraph	GenCopyModel (const int &Nodes, const double &Beta, TRnd &Rnd=TInt::Rnd)
	Generates a random scale-free network using the Copying Model. More...
PNGraph	GenRMat (const int &Nodes, const int &Edges, const double &A, const double &B, const double &C, TRnd &Rnd=TInt::Rnd)
	Generates a R-MAT graph using recursive descent into a 2x2 matrix [A,B; C, 1-(A+B+C)]. More...
PNGraph	GenRMatEpinions ()
	Generates a R-Mat graph, with a synthetic copy of the Epinions social network. More...
template<class PGraph >
PGraph	GenGrid (const int &Rows, const int &Cols, const bool &IsDir=true)
	Generates a 2D-grid graph of Rows rows and Cols columns. More...
template<class PGraph >
PGraph	GenStar (const int &Nodes, const bool &IsDir=true)
	Generates a graph with star topology. Node id 0 is in the center and then links to all other nodes. More...
template<class PGraph >
PGraph	GenCircle (const int &Nodes, const int &NodeOutDeg=1, const bool &IsDir=true)
	Generates a circle graph where every node creates out-links to NodeOutDeg forward nodes. More...
template<class PGraph >
PGraph	GenFull (const int &Nodes)
	Generates a complete graph on Nodes nodes. Graph has no self-loops. More...
template<class PGraph >
PGraph	GenTree (const int &Fanout, const int &Levels, const bool &IsDir=true, const bool &ChildPointsToParent=true)
	Generates a tree graph of Levels levels with every parent having Fanout children. More...
template<class PGraph >
PGraph	GenBaraHierar (const int &Levels, const bool &IsDir=true)
	Generates a Ravasz-Barabasi deterministic scale-free graph. More...
template<class PGraph >
PGraph	GenRndGnm (const int &Nodes, const int &Edges, const bool &IsDir=true, TRnd &Rnd=TInt::Rnd)
	Generates an Erdos-Renyi random graph. More...
PNGraph	LoadDyNet (const TStr &FNm)
	For more info see ORA Network Analysis Data (http://www.casos.cs.cmu.edu/computational_tools/data2.php) More...
TVec< PNGraph >	LoadDyNetGraphV (const TStr &FNm)
	For more info see ORA Network Analysis Data (http://www.casos.cs.cmu.edu/computational_tools/data2.php) More...
template<class PGraph >
PGraph	LoadEdgeList (const TStr &InFNm, const int &SrcColId=0, const int &DstColId=1)
	Loads a (directed, undirected or multi) graph from a text file InFNm with 1 edge per line (whitespace separated columns, integer node ids). More...
template<class PGraph >
PGraph	LoadEdgeList (const TStr &InFNm, const int &SrcColId, const int &DstColId, const char &Separator)
	Loads a (directed, undirected or multi) graph from a text file InFNm with 1 edge per line ('Separator' separated columns, integer node ids). More...
template<class PGraph >
PGraph	LoadEdgeListStr (const TStr &InFNm, const int &SrcColId=0, const int &DstColId=1)
	Loads a (directed, undirected or multi) graph from a text file InFNm with 1 edge per line (whitespace separated columns, arbitrary string node ids). More...
template<class PGraph >
PGraph	LoadEdgeListStr (const TStr &InFNm, const int &SrcColId, const int &DstColId, TStrHash< TInt > &StrToNIdH)
	Loads a (directed, undirected or multi) graph from a text file InFNm with 1 edge per line (whitespace separated columns, arbitrary string node ids). More...
template<class PGraph >
PGraph	LoadConnList (const TStr &InFNm)
	Loads a (directed, undirected or multi) graph from a text file InFNm with 1 node and all its edges in a single line. More...
template<class PGraph >
PGraph	LoadConnListStr (const TStr &InFNm, TStrHash< TInt > &StrToNIdH)
	Loads a (directed, undirected or multi) graph from a text file InFNm with 1 node and all its edges in a single line. More...
template<class PGraph >
PGraph	LoadPajek (const TStr &InFNm)
	Loads a (directed, undirected or multi) graph from Pajek .PAJ format file. More...
template<class PGraph >
void	SaveEdgeList (const PGraph &Graph, const TStr &OutFNm, const TStr &Desc=TStr())
	Saves a graph into a text file. Each line contains two columns and encodes a single edge: <source node="" id>=""><tab><destination node="" id>=""> More...
template<class PGraph >
void	SavePajek (const PGraph &Graph, const TStr &OutFNm)
	Saves a graph in a Pajek .NET format. More...
template<class PGraph >
void	SavePajek (const PGraph &Graph, const TStr &OutFNm, const TIntStrH &NIdColorH)
	Saves a graph in a Pajek .NET format. More...
template<class PGraph >
void	SavePajek (const PGraph &Graph, const TStr &OutFNm, const TIntStrH &NIdColorH, const TIntStrH &NIdLabelH)
	Saves a graph in a Pajek .NET format. More...
template<class PGraph >
void	SavePajek (const PGraph &Graph, const TStr &OutFNm, const TIntStrH &NIdColorH, const TIntStrH &NIdLabelH, const TIntStrH &EIdColorH)
	Saves a graph in a Pajek .NET format. More...
template<class PGraph >
void	SaveMatlabSparseMtx (const PGraph &Graph, const TStr &OutFNm)
	Saves a graph in a MATLAB sparse matrix format. More...
template<class PGraph >
void	SaveGViz (const PGraph &Graph, const TStr &OutFNm, const TStr &Desc=TStr(), const bool &NodeLabels=false, const TIntStrH &NIdColorH=TIntStrH())
	Save a graph in GraphVizp .DOT format. More...
template<class PGraph >
void	SaveGViz (const PGraph &Graph, const TStr &OutFNm, const TStr &Desc, const TIntStrH &NIdLabelH)
	Save a graph in GraphVizp .DOT format. More...
void	SetAllInvertSign (TFltV &ValV, const double &Val)
bool	IsAllValVNeg (TFltV &ValV, const bool &InvertSign)
void	GetSngVals (const PNGraph &Graph, const int &SngVals, TFltV &SngValV)
	Computes largest SngVals singular values of the adjacency matrix representing a directed Graph. More...
void	GetSngVec (const PNGraph &Graph, TFltV &LeftSV, TFltV &RightSV)
	Computes the leading left and right singular vector of the adjacency matrix representing a directed Graph. More...
void	GetSngVec (const PNGraph &Graph, const int &SngVecs, TFltV &SngValV, TVec< TFltV > &LeftSV, TVec< TFltV > &RightSV)
void	GetEigVals (const PUNGraph &Graph, const int &EigVals, TFltV &EigValV)
	Computes top EigVals eigenvalues of the adjacency matrix representing a given undirected Graph. More...
void	GetEigVec (const PUNGraph &Graph, TFltV &EigVecV)
	Computes the leading eigenvector of the adjacency matrix representing a given undirected Graph. More...
void	GetEigVec (const PUNGraph &Graph, const int &EigVecs, TFltV &EigValV, TVec< TFltV > &EigVecV)
	Computes top EigVecs eigenvalues and eigenvectors of the adjacency matrix representing a given undirected Graph. More...
void	GetInvParticipRat (const PUNGraph &Graph, int MaxEigVecs, int TimeLimit, TFltPrV &EigValIprV)
template<class PGraph >
void	DrawGViz (const PGraph &Graph, const TGVizLayout &Layout, const TStr &PltFNm, const TStr &Desc=TStr(), const bool &NodeLabels=false, const TIntStrH &NIdColorH=TIntStrH())
	Draws a given Graph using a selected GraphViz Layout engine with nodes colored. More...
template<class PGraph >
void	DrawGViz (const PGraph &Graph, const TGVizLayout &Layout, const TStr &PltFNm, const TStr &Desc, const TIntStrH &NodeLabelH)
	Draws a given Graph using a selected GraphViz Layout engine with nodes labeled. More...
template<class PGraph >
PGraph	GetKCore (const PGraph &Graph, const int &K)
void	PlotEigValRank (const PUNGraph &Graph, const int &EigVals, const TStr &FNmPref, TStr DescStr=TStr())
	Plots the eigen-value rank distribution of the Graph adjacency matrix. Plots first EigVals eigenvalues. More...
void	PlotEigValDistr (const PUNGraph &Graph, const int &EigVals, const TStr &FNmPref, TStr DescStr=TStr())
	Plots the distribution of components of the leading eigen-vector of the Graph adjacency matrix. Plots first EigVals values. More...
void	PlotInvParticipRat (const PUNGraph &Graph, const int &MaxEigVecs, const int &TimeLimit, const TStr &FNmPref, TStr DescStr)
void	PlotSngValRank (const PNGraph &Graph, const int &SngVals, const TStr &FNmPref, TStr DescStr=TStr())
	Plots the rank distribution of singular values of the Graph adjacency matrix. Plots first SngVals values. More...
void	PlotSngValDistr (const PNGraph &Graph, const int &SngVals, const TStr &FNmPref, TStr DescStr=TStr())
	Plots the rank distribution of singular values of the Graph adjacency matrix. Plots first SngVals values. More...
void	PlotSngVec (const PNGraph &Graph, const TStr &FNmPref, TStr DescStr=TStr())
	Plots the distribution of the values of the leading left singular vector of the Graph adjacency matrix. Plots first SngVals values. More...
template<class PGraph >
void	PlotInDegDistr (const PGraph &Graph, const TStr &FNmPref, TStr DescStr=TStr(), const bool &PlotCCdf=false, const bool &PowerFit=false)
template<class PGraph >
void	PlotOutDegDistr (const PGraph &Graph, const TStr &FNmPref, TStr DescStr=TStr(), const bool &PlotCCdf=false, const bool &PowerFit=false)
template<class PGraph >
void	PlotWccDistr (const PGraph &Graph, const TStr &FNmPref, TStr DescStr=TStr())
	Plots the distribution of sizes of weakly connected components of a Graph. More...
template<class PGraph >
void	PlotSccDistr (const PGraph &Graph, const TStr &FNmPref, TStr DescStr=TStr())
	Plots the distribution of sizes of strongly connected components of a Graph. More...
template<class PGraph >
void	PlotClustCf (const PGraph &Graph, const TStr &FNmPref, TStr DescStr=TStr())
	Plots the distribution of clustering coefficient of a Graph. More...
template<class PGraph >
void	PlotHops (const PGraph &Graph, const TStr &FNmPref, TStr DescStr=TStr(), const bool &IsDir=false, const int &NApprox=32)
template<class PGraph >
void	PlotShortPathDistr (const PGraph &Graph, const TStr &FNmPref, TStr DescStr=TStr(), int TestNodes=TInt::Mx)
	Plots the distribution of the shortest path lengths of a Graph. Implementation is based on BFS. More...
template<class PGraph >
void	PlotKCoreNodes (const PGraph &Graph, const TStr &FNmPref, TStr DescStr=TStr())
	Plots the k-Core node-size distribution: Core k vs. number of nodes in k-core. More...
template<class PGraph >
void	PlotKCoreEdges (const PGraph &Graph, const TStr &FNmPref, TStr DescStr=TStr())
	Plots the k-Core edge-size distribution: Core k vs. number of edges in k-core. More...
PUNGraph	GetSubGraph (const PUNGraph &Graph, const TIntV &NIdV, const bool &RenumberNodes=false)
	Returns an induced subgraph of an undirected graph Graph with NIdV nodes with an optional node renumbering. More...
PNGraph	GetSubGraph (const PNGraph &Graph, const TIntV &NIdV, const bool &RenumberNodes)
PUNGraph	GetEgonet (const PUNGraph &Graph, const int CtrNId, int &ArndEdges)
	Returns the egonet of node CtrNId as center in undirected graph Graph. And returns number of edges around the egonet. More...
PNGraph	GetEgonet (const PNGraph &Graph, const int CtrNId, int &InEdges, int &OutEdges)
	Returns the egonet of node CtrNId as center in directed graph Graph. And returns number of edges go in and out the egonet. More...
template<class PGraph >
PGraph	GetSubGraph (const PGraph &Graph, const TIntV &NIdV)
	Returns an induced subgraph of graph Graph with NIdV nodes. More...
template<class PGraph >
PGraph	GetESubGraph (const PGraph &Graph, const TIntV &EIdV)
	Returns a subgraph of graph Graph with EIdV edges. More...
template<class PGraph >
PGraph	GetESubGraph (const PGraph &Graph, const TIntPrV &EdgeV)
template<class PGraph , class TEdgeDat >
PGraph	GetEDatSubGraph (const PGraph &Graph, const TEdgeDat &EDat, const int &Cmp)
	Returns a subgraph of graph Graph with edges where edge data matches the parameters. More...
template<class PGraph , class TEdgeDat >
PGraph	GetEDatSubGraph (const PGraph &Graph, const TIntV &NIdV, const TEdgeDat &EDat, const int &Cmp)
	Returns a subgraph of graph Graph with NIdV nodes and edges where edge data matches the parameters. More...
template<class POutGraph , class PInGraph >
POutGraph	ConvertGraph (const PInGraph &InGraph, const bool &RenumberNodes=false)
	Performs conversion of graph InGraph with an optional node renumbering. More...
template<class POutGraph , class PInGraph >
POutGraph	ConvertSubGraph (const PInGraph &InGraph, const TIntV &NIdV, const bool &RenumberNodes=false)
	Returns an induced subgraph of graph InGraph with NIdV nodes with an optional node renumbering. More...
template<class POutGraph , class PInGraph >
POutGraph	ConvertESubGraph (const PInGraph &InGraph, const TIntV &EIdV, const bool &RenumberNodes=false)
	Returns a subgraph of graph InGraph with EIdV edges with an optional node renumbering. More...
template<class PGraph >
PGraph	GetRndSubGraph (const PGraph &Graph, const int &NNodes)
	Returns an induced random subgraph of graph Graph with NNodes nodes. More...
template<class PGraph >
PGraph	GetRndESubGraph (const PGraph &Graph, const int &NEdges)
	Returns a random subgraph of graph Graph with NEdges edges. More...
template<class PGraph >
double	GetClustCf (const PGraph &Graph, int SampleNodes=-1)
	Computes the average clustering coefficient as defined in Watts and Strogatz, Collective dynamics of 'small-world' networks. More...
template<class PGraph >
double	GetClustCf (const PGraph &Graph, TFltPrV &DegToCCfV, int SampleNodes=-1)
	Computes the distribution of average clustering coefficient. More...
template<class PGraph >
double	GetClustCf (const PGraph &Graph, TFltPrV &DegToCCfV, int64 &ClosedTriadsX, int64 &OpenTriadsX, int SampleNodes=-1)
	Computes the distribution of average clustering coefficient as well as the number of open and closed triads in the graph. More...
template<class PGraph >
double	GetNodeClustCf (const PGraph &Graph, const int &NId)
	Returns clustering coefficient of a particular node. More...
template<class PGraph >
void	GetNodeClustCf (const PGraph &Graph, TIntFltH &NIdCCfH)
	Computes clustering coefficient of each node of the Graph. More...
template<class PGraph >
int64	GetTriads (const PGraph &Graph, int SampleNodes=-1)
	Returns the number of triangles in a graph. More...
template<class PGraph >
void	GetTriads (const PGraph &Graph, TIntTrV &NIdCOTriadV, int SampleNodes=-1)
	Computes the number of open and close triads for every node of the network. More...
template<class PGraph >
int	GetTriadEdges (const PGraph &Graph, int SampleEdges=-1)
	Counts the number of edges that participate in at least one triad. More...
template<class PGraph >
int	GetNodeTriads (const PGraph &Graph, const int &NId)
	Returns the number of undirected triads a node NId participates in. More...
template<class PGraph >
int	GetNodeTriads (const PGraph &Graph, const int &NId, int &ClosedNTriadsX, int &OpenNTriadsX)
	Returns number of Open and Closed triads a node NId participates in. More...
template<class PGraph >
int	GetNodeTriads (const PGraph &Graph, const int &NId, const TIntSet &GroupSet, int &InGroupEdgesX, int &InOutGroupEdgesX, int &OutGroupEdgesX)
	Returns the number of triads between a node NId and a subset of its neighbors GroupSet. More...
template<class PGraph >
void	GetTriadParticip (const PGraph &Graph, TIntPrV &TriadCntV)
	Triangle Participation Ratio: For each node counts how many triangles it participates in and then returns a set of pairs (number of triangles, number of such nodes). More...
template<class PGraph >
int	GetCmnNbrs (const PGraph &Graph, const int &NId1, const int &NId2)
	Returns a number of shared neighbors between a pair of nodes NId1 and NId2. More...
template<class PGraph >
int	GetCmnNbrs (const PGraph &Graph, const int &NId1, const int &NId2, TIntV &NbrV)
	Returns the shared neighbors between a pair of nodes NId1 and NId2. More...
template<class PGraph >
int	GetLen2Paths (const PGraph &Graph, const int &NId1, const int &NId2)
	Returns the number of length 2 directed paths between a pair of nodes NId1, NId2 (NId1 –> U –> NId2). More...
template<class PGraph >
int	GetLen2Paths (const PGraph &Graph, const int &NId1, const int &NId2, TIntV &NbrV)
	Returns the 2 directed paths between a pair of nodes NId1, NId2 (NId1 –> U –> NId2). More...
template<>
int	GetCmnNbrs< PUNGraph > (const PUNGraph &Graph, const int &NId1, const int &NId2, TIntV &NbrV)

Detailed Description

Main namespace for all the Snap global entities.

Function Documentation

template<class PGraph >

void TSnap::AddSelfEdges

(

const PGraph &

Graph

)

Adds a self-edge to every node in the graph.

Definition at line 369 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), and TVec< TVal, TSizeTy >::Len().

                                       {
  TIntV EdgeV;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    const int NId = NI.GetId();
    if (! Graph->IsEdge(NId, NId)) {
      EdgeV.Add(NId);
    }
  }
  for (int i = 0; i < EdgeV.Len(); i++) {
    Graph->AddEdge(EdgeV[i], EdgeV[i]);
  }
}

Here is the call graph for this function:

const TStr TSnap::CapAttrName

(

"capacity"

)

Referenced by GetMaxFlowIntEK(), and TSnap::TPRManager::TPRManager().

Here is the caller graph for this function:

template<class PGraph >

int TSnap::CntDegNodes	(	const PGraph &	Graph,
		const int &	NodeDeg
	)

Returns the number of nodes with degree NodeDeg.

Definition at line 105 of file alg.h.

Referenced by TTimeNet::LoadArxiv(), TTimeNet::LoadPatents(), and TGStat::TakeBasicStat().

                                                         {
  int Cnt = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetDeg() == NodeDeg) Cnt++;
  }
  return Cnt;
}

Here is the caller graph for this function:

template<class PGraph >

int TSnap::CntEdgesToSet	(	const PGraph &	Graph,
		const int &	NId,
		const TIntSet &	NodeSet
	)

Returns the number of nodes in NodeSet that have an edge to the node NId.

Definition at line 123 of file alg.h.

References THashSet< TKey, THashFunc >::AddKey(), gfDirected, and THashSet< TKey, THashFunc >::IsKey().

                                                                               {
  if (! Graph->IsNode(NId)) { return 0; }
  const bool IsDir = Graph->HasFlag(gfDirected);
  const typename PGraph::TObj::TNodeI NI = Graph->GetNI(NId);
  if (! IsDir) {
    int EdgesToSet = 0;
    for (int e = 0; e < NI.GetOutDeg(); e++) {
      if (NodeSet.IsKey(NI.GetOutNId(e))) { EdgesToSet++; } }
    return EdgesToSet;
  } else {
    TIntSet Set(NI.GetDeg());
    for (int e = 0; e < NI.GetOutDeg(); e++) {
      if (NodeSet.IsKey(NI.GetOutNId(e))) { Set.AddKey(NI.GetOutNId(e)); } }
    for (int e = 0; e < NI.GetInDeg(); e++) {
      if (NodeSet.IsKey(NI.GetInNId(e))) { Set.AddKey(NI.GetInNId(e)); } }
    return Set.Len();
  }
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::CntInDegNodes	(	const PGraph &	Graph,
		const int &	NodeInDeg
	)

Returns the number of nodes with in-degree NodeInDeg.

Definition at line 87 of file alg.h.

Referenced by TTimeNet::LoadBipartite(), and TGStat::TakeBasicStat().

                                                             {
  int Cnt = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetInDeg() == NodeInDeg) Cnt++;
  }
  return Cnt;
}

Here is the caller graph for this function:

template<class PGraph >

int TSnap::CntNonZNodes

(

const PGraph &

Graph

)

Returns the number of nodes with degree greater than 0.

Definition at line 114 of file alg.h.

Referenced by TTimeNet::PlotMedianDegOverTm().

                                      {
  int Cnt = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetDeg() > 0) Cnt++;
  }
  return Cnt;
}

Here is the caller graph for this function:

template<class PGraph >

int TSnap::CntOutDegNodes	(	const PGraph &	Graph,
		const int &	NodeOutDeg
	)

Returns the number of nodes with out-degree NodeOutDeg.

Definition at line 96 of file alg.h.

Referenced by TTimeNet::LoadBipartite(), and TGStat::TakeBasicStat().

                                                               {
  int Cnt = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetOutDeg() == NodeOutDeg) Cnt++;
  }
  return Cnt;
}

Here is the caller graph for this function:

template<class PGraph >

int TSnap::CntSelfEdges

(

const PGraph &

Graph

)

Counts the number fo of self-edges in a graph. Edge (u,u) is a self-edge.

Definition at line 334 of file alg.h.

                                      {
  int Cnt = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    for (int e = 0; e < NI.GetOutDeg(); e++) {
      if (NI.GetId() == NI.GetOutNId(e)) { Cnt++; }
    }
  }
  return Cnt;
}

template<class PGraph >

int TSnap::CntUniqBiDirEdges

(

const PGraph &

Graph

)

Counts unique bidirectional edges in the graph Graph. Edge is bidirectional is there exist directed edges in both directions: (u,v) and (v,u)

Definition at line 316 of file alg.h.

References CntUniqUndirEdges(), and gfDirected.

Referenced by TGStat::TakeBasicStat().

                                           {
  if (! Graph->HasFlag(gfDirected)) { // graph is undirected
    return CntUniqUndirEdges(Graph);  // then every edge is bi-directional
  }
  TIntSet NbrSet;
  int Cnt = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    const int SrcId = NI.GetId();
    for (int e = 0; e < NI.GetOutDeg(); e++) {
      const int DstId = NI.GetOutNId(e);
      if (DstId <= SrcId) { continue; } // count each un-dir edge only once
      if (Graph->IsEdge(DstId, SrcId)) { Cnt++; }
    }
  }
  return Cnt;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

int TSnap::CntUniqDirEdges

(

const PGraph &

Graph

)

Counts unique directed edges in the graph Graph. Nodes (u,v)<.

> (where <code>u!=v</code>) are connected via an directted edge if there exists a directed edge from node \c u to node \c v. 

Definition at line 301 of file alg.h.

References THashSet< TKey, THashFunc >::AddKey(), THashSet< TKey, THashFunc >::Clr(), and THashSet< TKey, THashFunc >::Len().

Referenced by TGStat::TakeBasicStat().

                                         {
  TIntSet NbrSet;
  int Cnt = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    NbrSet.Clr(false);
    for (int e = 0; e < NI.GetOutDeg(); e++) { // unique out-neighbors of a node
      if (NI.GetOutNId(e) != NI.GetId()) { // skip self-edges
        NbrSet.AddKey(NI.GetOutNId(e)); }
    }
    Cnt += NbrSet.Len();
  }
  return Cnt;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

int TSnap::CntUniqUndirEdges

(

const PGraph &

Graph

)

Counts unique undirected edges in the graph Graph. Nodes (u,v)<.

> (where <code>u!=v</code>) are connected via an undirected edge if there exists an edge in either direction <code>(u,v)</code> or <code>(v,u)</code>. 

Definition at line 279 of file alg.h.

References THashSet< TKey, THashFunc >::AddKey(), THashSet< TKey, THashFunc >::Clr(), and THashSet< TKey, THashFunc >::Len().

Referenced by CntUniqBiDirEdges().

                                           {
  TIntSet NbrSet;
  TIntSet SelfNbrSet;
  int Cnt = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    NbrSet.Clr(false);
    for (int e = 0; e < NI.GetDeg(); e++) { // unique neighbors of a node
      const int NbrId = NI.GetNbrNId(e);
      if (NbrId == NI.GetId()) { // remember self-edges
        SelfNbrSet.AddKey(NbrId);
      } else {
        NbrSet.AddKey(NbrId);
      }
    }
    Cnt += NbrSet.Len();
  }
  // OP RS 2014/06/11 self-edges are currently not used 
  //return Cnt / 2 + SelfNbrSet.Len();
  return Cnt / 2;
}

Here is the call graph for this function:

Here is the caller graph for this function:

double TSnap::CommunityCNM	(	const PUNGraph &	Graph,
		TCnComV &	CmtyV
	)

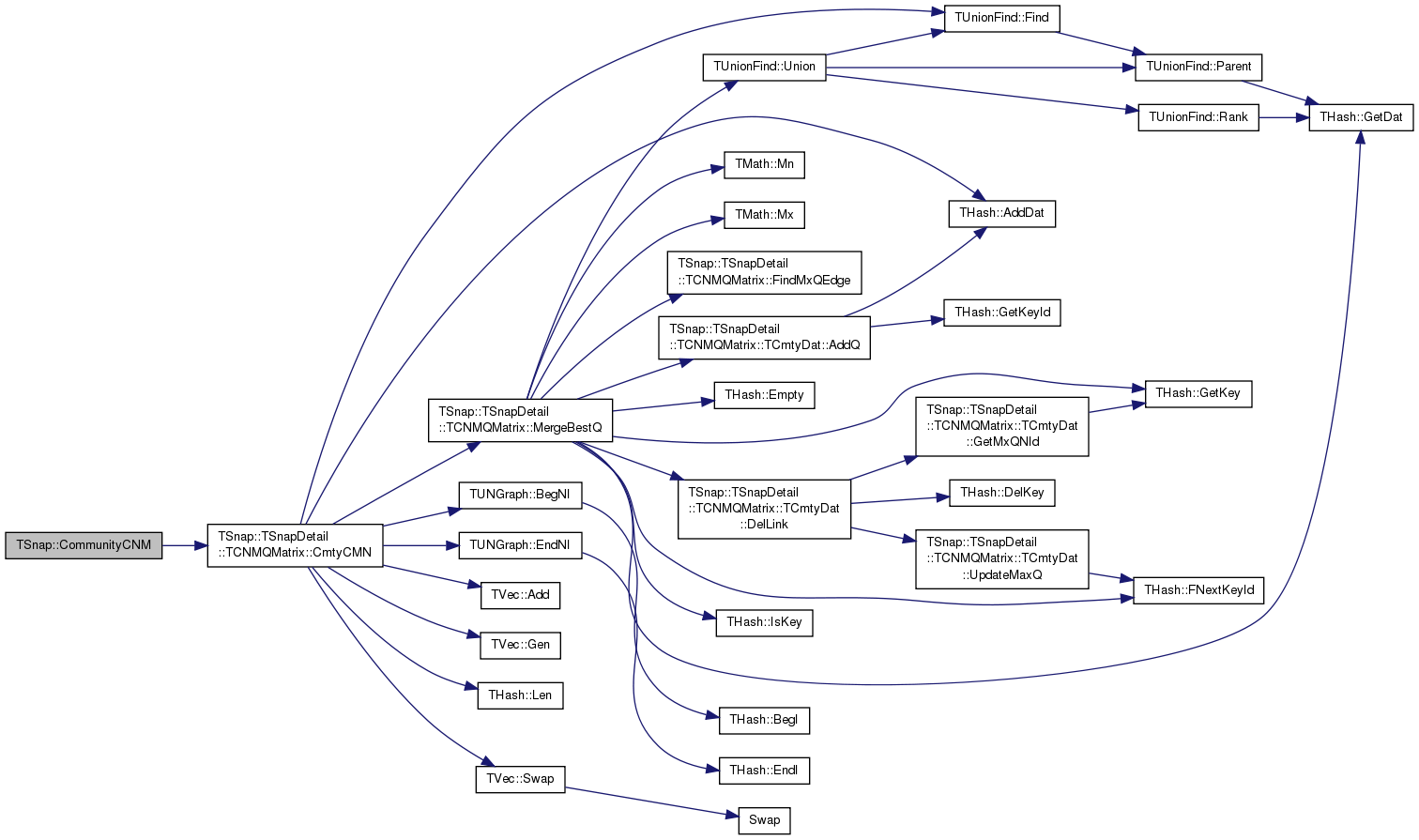
Clauset-Newman-Moore community detection method for large networks. At every step of the algorithm two communities that contribute maximum positive value to global modularity are merged. See: Finding community structure in very large networks, A. Clauset, M.E.J. Newman, C. Moore, 2004

Definition at line 304 of file cmty.cpp.

References TSnap::TSnapDetail::TCNMQMatrix::CmtyCMN().

                                                           {
  return TSnapDetail::TCNMQMatrix::CmtyCMN(Graph, CmtyV);
}

Here is the call graph for this function:

double TSnap::CommunityGirvanNewman	(	PUNGraph &	Graph,
		TCnComV &	CmtyV
	)

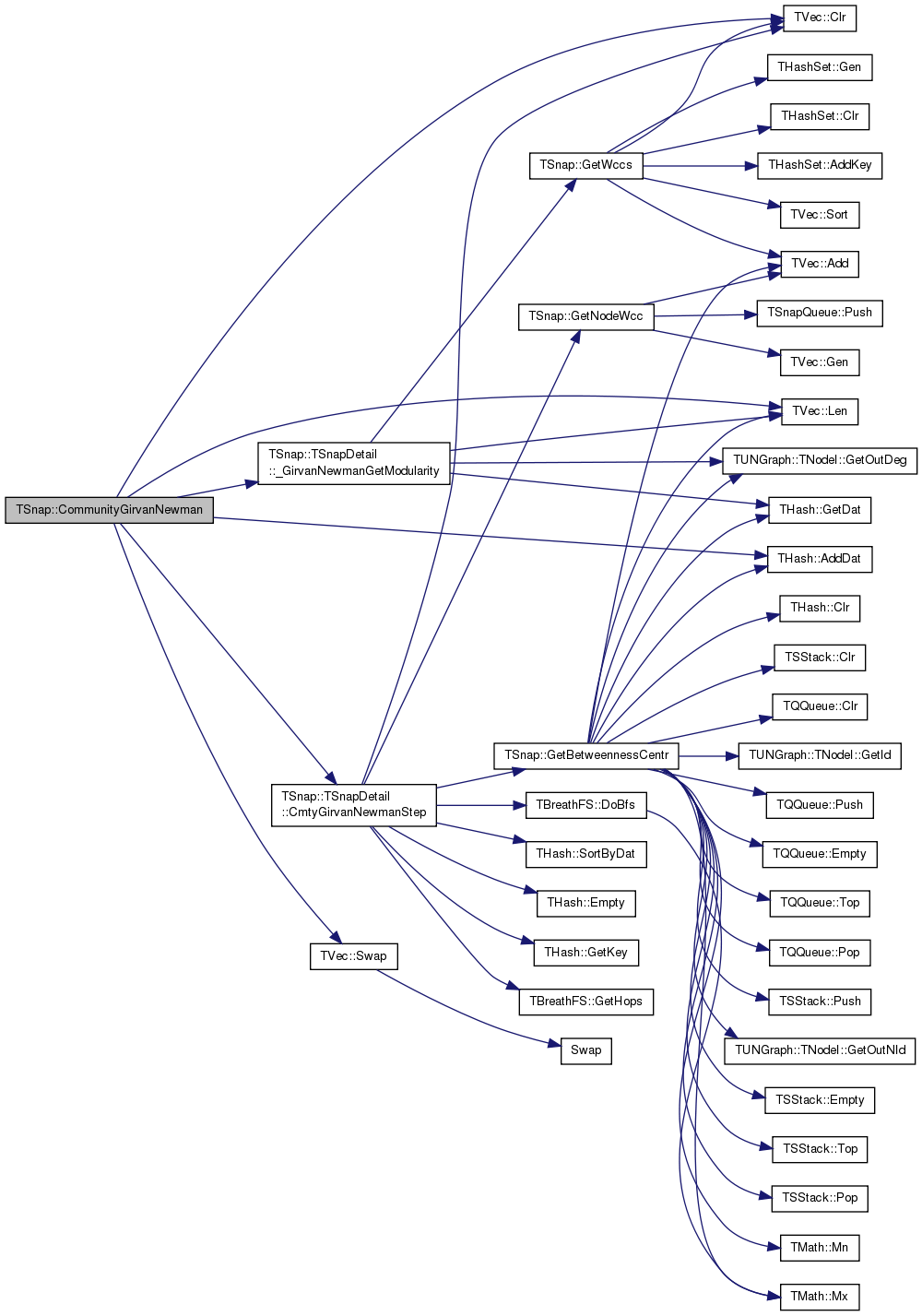
Girvan-Newman community detection algorithm based on Betweenness centrality. See: Girvan M. and Newman M. E. J., Community structure in social and biological networks, Proc. Natl. Acad. Sci. USA 99, 7821-7826 (2002)

Definition at line 98 of file cmty.cpp.

References TSnap::TSnapDetail::_GirvanNewmanGetModularity(), THash< TKey, TDat, THashFunc >::AddDat(), TVec< TVal, TSizeTy >::Clr(), TSnap::TSnapDetail::CmtyGirvanNewmanStep(), TVec< TVal, TSizeTy >::Len(), and TVec< TVal, TSizeTy >::Swap().

                                                              {
  TIntH OutDegH;
  const int NEdges = Graph->GetEdges();
  for (TUNGraph::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    OutDegH.AddDat(NI.GetId(), NI.GetOutDeg());
  }
  double BestQ = -1; // modularity
  TCnComV CurCmtyV;
  CmtyV.Clr();
  TIntV Cmty1, Cmty2;
  while (true) {
    TSnapDetail::CmtyGirvanNewmanStep(Graph, Cmty1, Cmty2);
    const double Q = TSnapDetail::_GirvanNewmanGetModularity(Graph, OutDegH, NEdges, CurCmtyV);
    //printf("current modularity: %f\n", Q);
    if (Q > BestQ) {
      BestQ = Q; 
      CmtyV.Swap(CurCmtyV);
    }
    if (Cmty1.Len()==0 || Cmty2.Len() == 0) { break; }
  }
  return BestQ;
}

Here is the call graph for this function:

template<class POutGraph , class PInGraph >

POutGraph TSnap::ConvertESubGraph	(	const PInGraph &	InGraph,
		const TIntV &	EIdV,
		const bool &	RenumberNodes = false
	)

Returns a subgraph of graph InGraph with EIdV edges with an optional node renumbering.

Creates a subgraph of the input graph InGraph on EIdV edges and returns an output graph. Input and output graphs can have different types. Node and edge data is not copied, but it is shared by input and output graphs.

Parameter RenumberNodes determines, whether the node IDs are preserved or not. If RenumberNodes is false, then nodes in the resulting graph have the same node IDs as nodes in InGraph. If RenumberNodes is true, then nodes in the resulting graph are renumbered sequentially from 0 to N-1. By default, the nodes are not renumbered.

Definition at line 403 of file subgraph.h.

References CAssert, gfMultiGraph, HasGraphFlag, IAssert, and TVec< TVal, TSizeTy >::Len().

                                                                                                  {
  CAssert(HasGraphFlag(typename PInGraph::TObj, gfMultiGraph)); // needs to have explicit edges
  POutGraph NewGraphPt = POutGraph::TObj::New();
  typename POutGraph::TObj& NewGraph = *NewGraphPt;
  NewGraph.Reserve(-1, EIdV.Len());
  if (! RenumberNodes) {
    for (int edge = 0; edge < EIdV.Len(); edge++) {
      const int EId = EIdV[edge];
      IAssert(InGraph->IsEdge(EId));
      const typename PInGraph::TObj::TEdgeI EI = InGraph->GetEI(EId);
      const int SrcNId = EI.GetSrcNId();
      const int DstNId = EI.GetDstNId();
      if (! NewGraph.IsNode(SrcNId)) {
        NewGraph.AddNode(SrcNId); }
      if (! NewGraph.IsNode(DstNId)) {
        NewGraph.AddNode(DstNId); }
      NewGraph.AddEdge(SrcNId, DstNId);
    }
  } else {
    // renumber nodes so that node ids are 0...N-1
    TIntSet NIdSet(InGraph->GetNodes());
    for (int edge = 0; edge < EIdV.Len(); edge++) {
      const int EId = EIdV[edge];
      IAssert(InGraph->IsEdge(EId));
      const typename PInGraph::TObj::TEdgeI EI = InGraph->GetEI(EId);
      const int SrcNId = NIdSet.AddKey(EI.GetSrcNId()); // map node ids
      const int DstNId = NIdSet.AddKey(EI.GetDstNId());
      if (! NewGraph.IsNode(SrcNId)) {
        NewGraph.AddNode(SrcNId); }
      if (! NewGraph.IsNode(DstNId)) {
        NewGraph.AddNode(DstNId); }
      NewGraph.AddEdge(SrcNId, DstNId);
    }
  }
  return NewGraphPt;
}

Here is the call graph for this function:

template<class POutGraph , class PInGraph >

POutGraph TSnap::ConvertGraph	(	const PInGraph &	InGraph,
		const bool &	RenumberNodes = false
	)

Performs conversion of graph InGraph with an optional node renumbering.

Takes an input graph InGraph and returns an output graph. Input and output graphs can have different types. Node and edge data is not copied, but it is shared by input and output graphs.

Parameter RenumberNodes determines, whether the node IDs are preserved or not. If RenumberNodes is false, then nodes in the resulting graph have the same node IDs as nodes in InGraph. If RenumberNodes is true, then nodes in the resulting graph are renumbered sequentially from 0 to N-1. By default, the nodes are not renumbered.

Definition at line 288 of file subgraph.h.

References THashSet< TKey, THashFunc >::AddKey(), gfDirected, and HasGraphFlag.

                                                                           {
  POutGraph OutGraphPt = POutGraph::TObj::New();
  typename POutGraph::TObj& OutGraph = *OutGraphPt;
  OutGraph.Reserve(InGraph->GetNodes(), InGraph->GetEdges());
  if (! RenumberNodes) {
    for (typename PInGraph::TObj::TNodeI NI = InGraph->BegNI(); NI < InGraph->EndNI(); NI++) {
      OutGraph.AddNode(NI.GetId());
    }
    for (typename PInGraph::TObj::TEdgeI EI = InGraph->BegEI(); EI < InGraph->EndEI(); EI++) {
      OutGraph.AddEdge(EI.GetSrcNId(), EI.GetDstNId());
      if (! HasGraphFlag(typename PInGraph::TObj, gfDirected) && HasGraphFlag(typename POutGraph::TObj, gfDirected)) { // add edge in the other direction
        OutGraph.AddEdge(EI.GetDstNId(), EI.GetSrcNId()); }
    }
  } else { // renumber nodes so that node ids are 0...N-1
    TIntSet NIdSet(InGraph->GetNodes());
    for (typename PInGraph::TObj::TNodeI NI = InGraph->BegNI(); NI < InGraph->EndNI(); NI++) {
      const int nid = NIdSet.AddKey(NI.GetId());
      OutGraph.AddNode(nid);
    }
    for (typename PInGraph::TObj::TEdgeI EI = InGraph->BegEI(); EI < InGraph->EndEI(); EI++) {
      const int SrcNId = NIdSet.GetKeyId(EI.GetSrcNId());
      const int DstNId = NIdSet.GetKeyId(EI.GetDstNId());
      OutGraph.AddEdge(SrcNId, DstNId);
      if (! HasGraphFlag(typename PInGraph::TObj, gfDirected) && HasGraphFlag(typename POutGraph::TObj, gfDirected)) {
        OutGraph.AddEdge(DstNId, SrcNId); }
    }
  }
  //OutGraph.Defrag();
  return OutGraphPt;
}

Here is the call graph for this function:

template<class POutGraph , class PInGraph >

POutGraph TSnap::ConvertSubGraph	(	const PInGraph &	InGraph,
		const TIntV &	NIdV,
		const bool &	RenumberNodes = false
	)

Returns an induced subgraph of graph InGraph with NIdV nodes with an optional node renumbering.

Creates a subgraph of the input graph InGraph on NIdV nodes and returns an output graph. Input and output graphs can have different types. Node and edge data is not copied, but it is shared by input and output graphs.

Parameter RenumberNodes determines, whether the node IDs are preserved or not. If RenumberNodes is false, then nodes in the resulting graph have the same node IDs as nodes in InGraph. If RenumberNodes is true, then nodes in the resulting graph are renumbered sequentially from 0 to N-1. By default, the nodes are not renumbered.

Definition at line 398 of file subgraph.h.

                                                                                                 {
  return TSnapDetail::TConvertSubGraph<POutGraph, PInGraph, HasGraphFlag(typename PInGraph::TObj, gfMultiGraph)>::Do(InGraph, NIdV, RenumberNodes);
}

template<class PGraph >

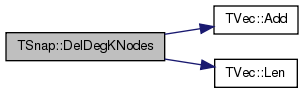
void TSnap::DelDegKNodes	(	PGraph &	Graph,
		const int &	OutDegK,
		const int &	InDegK
	)

Removes all the node of out-degree OutDegK and all the nodes of in-degree InDegK from the graph.

Definition at line 445 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), and TVec< TVal, TSizeTy >::Len().

                                                                        {
  TIntV DelNIdV;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetOutDeg() == OutDegK || NI.GetInDeg() == InDegK) {
      DelNIdV.Add(NI.GetId());
    }
  }
  for (int i = 0; i < DelNIdV.Len(); i++) {
    Graph->DelNode(DelNIdV[i]);
  }
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::DelNodes	(	PGraph &	Graph,
		const TIntV &	NIdV
	)

Removes nodes with ids stored in NIdV from the graph.

Definition at line 425 of file alg.h.

References TVec< TVal, TSizeTy >::Len().

                                                {
  for (int n = 0; n < NIdV.Len(); n++) {
    Graph->DelNode(NIdV[n]);
  }
}

Here is the call graph for this function:

template<class PGraph >

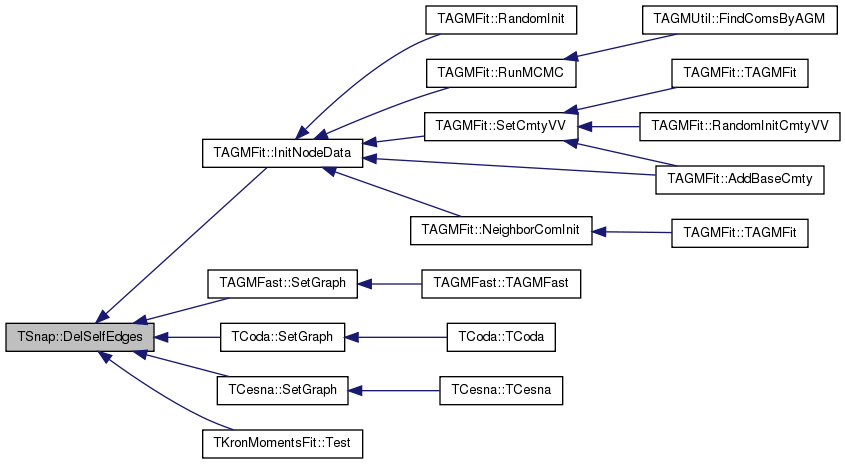
void TSnap::DelSelfEdges

(

const PGraph &

Graph

)

Removes all the self-edges from the graph.

Definition at line 419 of file alg.h.

Referenced by TAGMFit::InitNodeData(), TAGMFast::SetGraph(), TCoda::SetGraph(), TCesna::SetGraph(), and TKronMomentsFit::Test().

                                       {
  TSnapDetail::TDelSelfEdges<PGraph, HasGraphFlag(typename PGraph::TObj, gfMultiGraph)>
    ::Do(Graph);
}

Here is the caller graph for this function:

template<class PGraph >

void TSnap::DelZeroDegNodes

(

PGraph &

Graph

)

Removes all the zero-degree nodes, that isolated nodes, from the graph.

Definition at line 432 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), and TVec< TVal, TSizeTy >::Len().

Referenced by TKronMtx::PlotCmpGraphs(), and TMAGFitBern::PlotProperties().

                                    {
  TIntV DelNIdV;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetDeg() == 0) {
      DelNIdV.Add(NI.GetId());
    }
  }
  for (int i = 0; i < DelNIdV.Len(); i++) {
    Graph->DelNode(DelNIdV[i]);
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::DrawGViz	(	const PGraph &	Graph,
		const TGVizLayout &	Layout,
		const TStr &	PltFNm,
		const TStr &	Desc = TStr(),
		const bool &	NodeLabels = false,
		const TIntStrH &	NIdColorH = TIntStrH()
	)

Draws a given Graph using a selected GraphViz Layout engine with nodes colored.

Useful for drawing small (<100 node) graphs.

Parameters

PltFNm	Output filename (extension .ps, .png, .gif) determines the output format.
NIdColorH	Maps node ids to node colors (see GraphViz documentation for more details).

Definition at line 34 of file gviz.h.

References TStr::GetFExt(), TStr::GetSubStr(), TSnap::TSnapDetail::GVizDoLayout(), TStr::Len(), and SaveGViz().

Referenced by TLocClust::DrawWhiskers(), and PlotRoles().

                                                                                                                                                       {
  const TStr Ext = PltFNm.GetFExt();
  const TStr GraphFNm = PltFNm.GetSubStr(0, PltFNm.Len()-Ext.Len()) + "dot";
  SaveGViz(Graph, GraphFNm, Desc, NodeLabels, NIdColorH);
  TSnap::TSnapDetail::GVizDoLayout(GraphFNm, PltFNm, Layout);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::DrawGViz	(	const PGraph &	Graph,
		const TGVizLayout &	Layout,
		const TStr &	PltFNm,
		const TStr &	Desc,
		const TIntStrH &	NodeLabelH
	)

Draws a given Graph using a selected GraphViz Layout engine with nodes labeled.

Useful for drawing small (<100 node) graphs.

Parameters

PltFNm	Output filename (extension .ps, .png, .gif) determines the output format.
NIdColorH	Maps node ids to node colors (see GraphViz documentation for more details).

Definition at line 42 of file gviz.h.

References TStr::GetFExt(), TStr::GetSubStr(), TSnap::TSnapDetail::GVizDoLayout(), TStr::Len(), and SaveGViz().

                                                                                                                                {
  const TStr Ext = PltFNm.GetFExt();
  const TStr GraphFNm = PltFNm.GetSubStr(0, PltFNm.Len()-Ext.Len()) + "dot";
  SaveGViz(Graph, GraphFNm, Desc, NodeLabelH);
  TSnap::TSnapDetail::GVizDoLayout(GraphFNm, PltFNm, Layout);
}

Here is the call graph for this function:

int TSnap::FindAugV	(	const PNEANet &	Net,
		const int &	CapIndex,
		TIntV &	Flow,
		TIntQ &	FwdNodeQ,
		TIntH &	PredEdgeH,
		TIntQ &	BwdNodeQ,
		TIntH &	SuccEdgeH,
		TIntV &	MidToSrcAugV,
		TIntV &	MidToSnkAugV,
		const int &	SrcNId,
		const int &	SnkNId
	)

Returns the amount the flow can be augmented over the paths, 0 if no path can be found.

Find the augmenting path. Calls bidirectional BFS to find the path, and then builds the two path vectors.

Parameters

MidToSrcAugV	Contains the path vector from the midpoint node where the bi-d search met back to the source node.
MidToSnkAugV	Contains the path vector from the midpoint node where the bi-d search met back to the sink node.

Definition at line 71 of file flow.cpp.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::GetDat(), TNEANet::TEdgeI::GetDstNId(), TNEANet::TEdgeI::GetSrcNId(), IntFlowBiDBFS(), and TInt::Mx.

Referenced by GetMaxFlowIntEK().

                                                                                                                                                                                                                          {
  int MidPtNId = IntFlowBiDBFS(Net, CapIndex, Flow, FwdNodeQ, PredEdgeH, BwdNodeQ, SuccEdgeH, SrcNId, SnkNId);
  if (MidPtNId == -1) { return 0; }
  int MinAug = TInt::Mx, NId = MidPtNId, AugFlow = 0;
  // Build the path from the midpoint back to the source by tracing through the PredEdgeH
  for (int EId = PredEdgeH.GetDat(NId); NId != SrcNId; EId = PredEdgeH.GetDat(NId)) {
    MidToSrcAugV.Add(EId);
    const TNEANet::TEdgeI &EI = Net->GetEI(EId);
    if (EI.GetSrcNId() == NId) {
      NId = EI.GetDstNId();
      AugFlow = Flow[EId];
    } else {
      NId = EI.GetSrcNId();
      AugFlow = Net->GetIntAttrIndDatE(EId, CapIndex) - Flow[EId];
    }
    if (AugFlow < MinAug) { MinAug = AugFlow; }
  }
  NId = MidPtNId;
  // Build the path from the midpoint back to the sink by tracing through the SuccEdgeH
  for (int EId = SuccEdgeH.GetDat(NId); NId != SnkNId; EId = SuccEdgeH.GetDat(NId)) {
    MidToSnkAugV.Add(EId);
    const TNEANet::TEdgeI &EI = Net->GetEI(EId);
    if (EI.GetDstNId() == NId) {
      NId = EI.GetSrcNId();
      AugFlow = Flow[EId];
    } else {
      NId = EI.GetDstNId();
      AugFlow = Net->GetIntAttrIndDatE(EId, CapIndex) - Flow[EId];
    }
    if (AugFlow < MinAug) { MinAug = AugFlow; }
  }
  return MinAug;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

PGraph TSnap::GenBaraHierar	(	const int &	Levels,
		const bool &	IsDir
	)

Generates a Ravasz-Barabasi deterministic scale-free graph.

Corners of the graph are recursively expanded with miniature copies of the base graph (below). The graph has power-law degree distribution with the exponent 1+ln(5)/ln(4) and clustering coefficient with power-law decay exponent -1. Base graph:

///   o---o
///   |\ /|
///   | o |
///   |/ \|
///   o---o
/// 

See: Hierarchical organization in complex networks. Ravasz and Barabasi. URL: http://arxiv.org/abs/cond-mat/0206130

Definition at line 174 of file ggen.h.

References TMath::Power(), and TMath::Round().

                                                           {
  const int Nodes = (int) TMath::Round(TMath::Power(5, Levels));
  PGraph GraphPt = PGraph::New();
  typename PGraph::TObj& Graph = *GraphPt;
  Graph.Reserve(Nodes, -1);
  // base graph
  for (int i = 0; i < 5; i++) { Graph.AddNode(i); }
  Graph.AddEdge(1,2);  Graph.AddEdge(2,3);
  Graph.AddEdge(3,4);  Graph.AddEdge(4,1);
  Graph.AddEdge(1,0);  Graph.AddEdge(3,0);
  Graph.AddEdge(2,0);  Graph.AddEdge(4,0);
  // expansion
  const int CenterId = 0;
  for (int lev = 1; lev < Levels+1; lev++) {
    const int MxNId = Graph.GetNodes();
    // make 4 duplicate copies
    for (int d = 0; d < 4; d++) {
      for (int n = 0; n < MxNId; n++) { Graph.AddNode(); }
      for (int n = 0; n < MxNId; n++) {
        typename PGraph::TObj::TNodeI NI = Graph.GetNI(n);
        const int SrcId = n+MxNId*(d+1);
        for (int e = 0; e < NI.GetOutDeg(); e++) {
          Graph.AddEdge(SrcId, NI.GetOutNId(e)+MxNId*(d+1));
        }
      }
    }
    // add edges to the center
    //const int LevPow = (int)TMath::Round(TMath::Power(5,lev-1));
    for (int n = MxNId; n < Graph.GetNodes(); n++) {
      typename PGraph::TObj::TNodeI NI = Graph.GetNI(n);
      const int SrcId = n;
      int Pow = 1;  bool Skip = false;
      for (int p = 1; p <= lev; p++) {
        if (SrcId % (5*Pow) < Pow) { Skip=true; break; }
        Pow *= 5;
      }
      if (Skip) { continue; }
      Graph.AddEdge(SrcId, CenterId);
    }
  }
  return GraphPt;
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::GenCircle	(	const int &	Nodes,
		const int &	NodeOutDeg = 1,
		const bool &	IsDir = true
	)

Generates a circle graph where every node creates out-links to NodeOutDeg forward nodes.

Definition at line 104 of file ggen.h.

References gfDirected.

                                                                             {
  PGraph Graph = PGraph::TObj::New();
  Graph->Reserve(Nodes, Nodes*NodeOutDeg);
  for (int n = 0; n < Nodes; n++) {
    Graph->AddNode(n); }
  for (int n = 0; n < Nodes; n++) {
    for (int x = 0; x < NodeOutDeg; x++) {
      Graph->AddEdge(n, (n+x+1) % Nodes);
      if (Graph->HasFlag(gfDirected) && ! IsDir) { Graph->AddEdge((n+x+1) % Nodes, n); }
    }
  }
  return Graph;
}

PUNGraph TSnap::GenConfModel	(	const TIntV &	DegSeqV,
		TRnd &	Rnd
	)

Generates a random undirect graph with a given degree sequence.

Generates a random undirect graph with a given degree sequence DegSeqV. Configuration model operates as follows. For each node N, of degree DeqSeqV[N] we create DeqSeqV[N] spokes (half-edges). We then pick two spokes at random, and connect the spokes endpoints. We continue this process until no spokes are left. Generally this generates a multigraph (i.e., spokes out of same nodes can be chosen multiple times).We ignore (discard) self-loops and multiple edges. Thus, the generated graph will only approximate follow the given degree sequence. The method is very fast!

Definition at line 119 of file ggen.cpp.

References TUNGraph::AddEdge(), THashSet< TKey, THashFunc >::AddKey(), TUNGraph::AddNode(), TRnd::GetUniDevInt(), THashSet< TKey, THashFunc >::IsKey(), TVec< TVal, TSizeTy >::Len(), TMath::Mn(), TUNGraph::New(), TUNGraph::Reserve(), and Swap().

Referenced by GenConfModel(), GenRndPowerLaw(), and TTimeNet::PlotEffDiam().

                                                       {
  const int Nodes = DegSeqV.Len();
  PUNGraph GraphPt = TUNGraph::New();
  TUNGraph& Graph = *GraphPt;
  Graph.Reserve(Nodes, -1);
  TIntV NIdDegV(DegSeqV.Len(), 0);
  int DegSum=0, edges=0;
  for (int node = 0; node < Nodes; node++) {
    Graph.AddNode(node);
    for (int d = 0; d < DegSeqV[node]; d++) { NIdDegV.Add(node); }
    DegSum += DegSeqV[node];
  }
  NIdDegV.Shuffle(Rnd);
  TIntPrSet EdgeH(DegSum/2); // set of all edges, is faster than graph edge lookup
  if (DegSum % 2 != 0) {
    printf("Seg seq is odd [%d]: ", DegSeqV.Len());
    for (int d = 0; d < TMath::Mn(100, DegSeqV.Len()); d++) { printf("  %d", (int)DegSeqV[d]); }
    printf("\n");
  }
  int u=0, v=0;
  for (int c = 0; NIdDegV.Len() > 1; c++) {
    u = Rnd.GetUniDevInt(NIdDegV.Len());
    while ((v = Rnd.GetUniDevInt(NIdDegV.Len())) == u) { }
    if (u > v) { Swap(u, v); }
    const int E1 = NIdDegV[u];
    const int E2 = NIdDegV[v];
    if (v == NIdDegV.Len()-1) { NIdDegV.DelLast(); } 
    else { NIdDegV[v] = NIdDegV.Last();  NIdDegV.DelLast(); }
    if (u == NIdDegV.Len()-1) { NIdDegV.DelLast(); } 
    else { NIdDegV[u] = NIdDegV.Last();  NIdDegV.DelLast(); }
    if (E1 == E2 || EdgeH.IsKey(TIntPr(E1, E2))) { continue; }
    EdgeH.AddKey(TIntPr(E1, E2));
    Graph.AddEdge(E1, E2);
    edges++;
    if (c % (DegSum/100+1) == 0) { printf("\r configuration model: iter %d: edges: %d, left: %d", c, edges, NIdDegV.Len()/2); }
  }
  printf("\n");
  return GraphPt;
}

Here is the call graph for this function:

Here is the caller graph for this function:

PUNGraph TSnap::GenConfModel

(

const PUNGraph &

G

)

Generate a random graph using (approximately) the same node degrees as in G using the configuration model.

Definition at line 335 of file ggen.cpp.

References GenConfModel(), and GetDegSeqV().

                                         {
  TIntV DegSeqV(G->GetNodes(), 0);
  TSnap::GetDegSeqV(G, DegSeqV);
  return TSnap::GenConfModel(DegSeqV);
}

Here is the call graph for this function:

PNGraph TSnap::GenCopyModel	(	const int &	Nodes,
		const double &	Beta,
		TRnd &	Rnd
	)

Generates a random scale-free network using the Copying Model.

Generates a random scale-free network using the Copying Model. The generating process operates as follows: Node u is added to a graph, it selects a random node v, and with prob Beta it links to v, with 1-Beta links u links to neighbor of v. The power-law degree exponent is -1/(1-Beta). See: Stochastic models for the web graph. Kumar, Raghavan, Rajagopalan, Sivakumar, Tomkins, Upfal. URL: http://snap.stanford.edu/class/cs224w-readings/kumar00stochastic.pdf

Definition at line 453 of file ggen.cpp.

References TNGraph::AddEdge(), TNGraph::AddNode(), TNGraph::GetNI(), TNGraph::TNodeI::GetOutDeg(), TNGraph::TNodeI::GetOutNId(), TNGraph::GetRndNId(), TRnd::GetUniDev(), TRnd::GetUniDevInt(), TNGraph::New(), and TNGraph::Reserve().

                                                                      {
  PNGraph GraphPt = TNGraph::New();
  TNGraph& Graph = *GraphPt;
  Graph.Reserve(Nodes, Nodes);
  const int startNId = Graph.AddNode();
  Graph.AddEdge(startNId, startNId);
  for (int n = 1; n < Nodes; n++) {
    const int rnd = Graph.GetRndNId();
    const int NId = Graph.AddNode();
    if (Rnd.GetUniDev() < Beta) {
      Graph.AddEdge(NId, rnd); }
    else {
      const TNGraph::TNodeI NI = Graph.GetNI(rnd);
      const int rnd2 = Rnd.GetUniDevInt(NI.GetOutDeg());
      Graph.AddEdge(NId, NI.GetOutNId(rnd2));
    }
  }
  return GraphPt;
}

Here is the call graph for this function:

PUNGraph TSnap::GenDegSeq	(	const TIntV &	DegSeqV,
		TRnd &	Rnd
	)

Generates a random graph with exact degree sequence.

Generates a random graph with exact degree sequence DegSeqV. The generated graph has no self loops. The graph generation process simulates the Configuration Model but if a duplicate edge occurs, we find a random edge, break it and reconnect it with the duplicate.

Definition at line 58 of file ggen.cpp.

References TUNGraph::AddEdge(), TUNGraph::AddNode(), TUNGraph::DelEdge(), TSnap::TSnapDetail::GetRndEdgeNonAdjNode(), IAssert, IAssertR, TUNGraph::IsEdge(), TVec< TVal, TSizeTy >::IsSorted(), TVec< TVal, TSizeTy >::Len(), TUNGraph::New(), TUNGraph::Reserve(), TInt::Rnd, TPair< TVal1, TVal2 >::Val1, and TPair< TVal1, TVal2 >::Val2.

Referenced by GenRndDegK(), and GenRndPowerLaw().

                                                    {
  const int Nodes = DegSeqV.Len();
  PUNGraph GraphPt = TUNGraph::New();
  TUNGraph& Graph = *GraphPt;
  Graph.Reserve(Nodes, -1);
  TIntH DegH(DegSeqV.Len(), true);
  
  IAssertR(DegSeqV.IsSorted(false), "DegSeqV must be sorted in descending order.");
  int DegSum=0, edge=0;
  for (int node = 0; node < Nodes; node++) {
    IAssert(Graph.AddNode(node) == node);
    DegH.AddDat(node, DegSeqV[node]);
    DegSum += DegSeqV[node];
  }
  IAssert(DegSum % 2 == 0);
  while (! DegH.Empty()) {
    // pick random nodes and connect
    const int NId1 = DegH.GetKey(DegH.GetRndKeyId(TInt::Rnd, 0.5));
    const int NId2 = DegH.GetKey(DegH.GetRndKeyId(TInt::Rnd, 0.5));
    IAssert(DegH.IsKey(NId1) && DegH.IsKey(NId2));
    if (NId1 == NId2) {
      if (DegH.GetDat(NId1) == 1) { continue; }
      // find rnd edge, break it, and connect the endpoints to the nodes
      const TIntPr Edge = TSnapDetail::GetRndEdgeNonAdjNode(GraphPt, NId1, -1);
      if (Edge.Val1==-1) { continue; }
      Graph.DelEdge(Edge.Val1, Edge.Val2);
      Graph.AddEdge(Edge.Val1, NId1);
      Graph.AddEdge(NId1, Edge.Val2);
      if (DegH.GetDat(NId1) == 2) { DegH.DelKey(NId1); }
      else { DegH.GetDat(NId1) -= 2; }
    } else {
      if (! Graph.IsEdge(NId1, NId2)) {
        Graph.AddEdge(NId1, NId2); }  // good edge
      else {
        // find rnd edge, break and cross-connect
        const TIntPr Edge = TSnapDetail::GetRndEdgeNonAdjNode(GraphPt, NId1, NId2);
        if (Edge.Val1==-1) {continue; }
        Graph.DelEdge(Edge.Val1, Edge.Val2);
        Graph.AddEdge(NId1, Edge.Val1);
        Graph.AddEdge(NId2, Edge.Val2);
      }
      if (DegH.GetDat(NId1)==1) { DegH.DelKey(NId1); }
      else { DegH.GetDat(NId1) -= 1; }
      if (DegH.GetDat(NId2)==1) { DegH.DelKey(NId2); }
      else { DegH.GetDat(NId2) -= 1; }
    }
    if (++edge % 1000 == 0) {
      printf("\r %dk / %dk", edge/1000, DegSum/2000); }
  }
  return GraphPt;
}

Here is the call graph for this function:

Here is the caller graph for this function:

PNGraph TSnap::GenForestFire	(	const int &	Nodes,
		const double &	FwdProb,
		const double &	BckProb
	)

Generates a random Forest Fire, directed graph with given probabilities.

Definition at line 442 of file ggen.cpp.

References TForestFire::GenGraph().

                                                                                      {
  return TForestFire::GenGraph(Nodes, FwdProb, BckProb);
}

Here is the call graph for this function:

template<class PGraph >

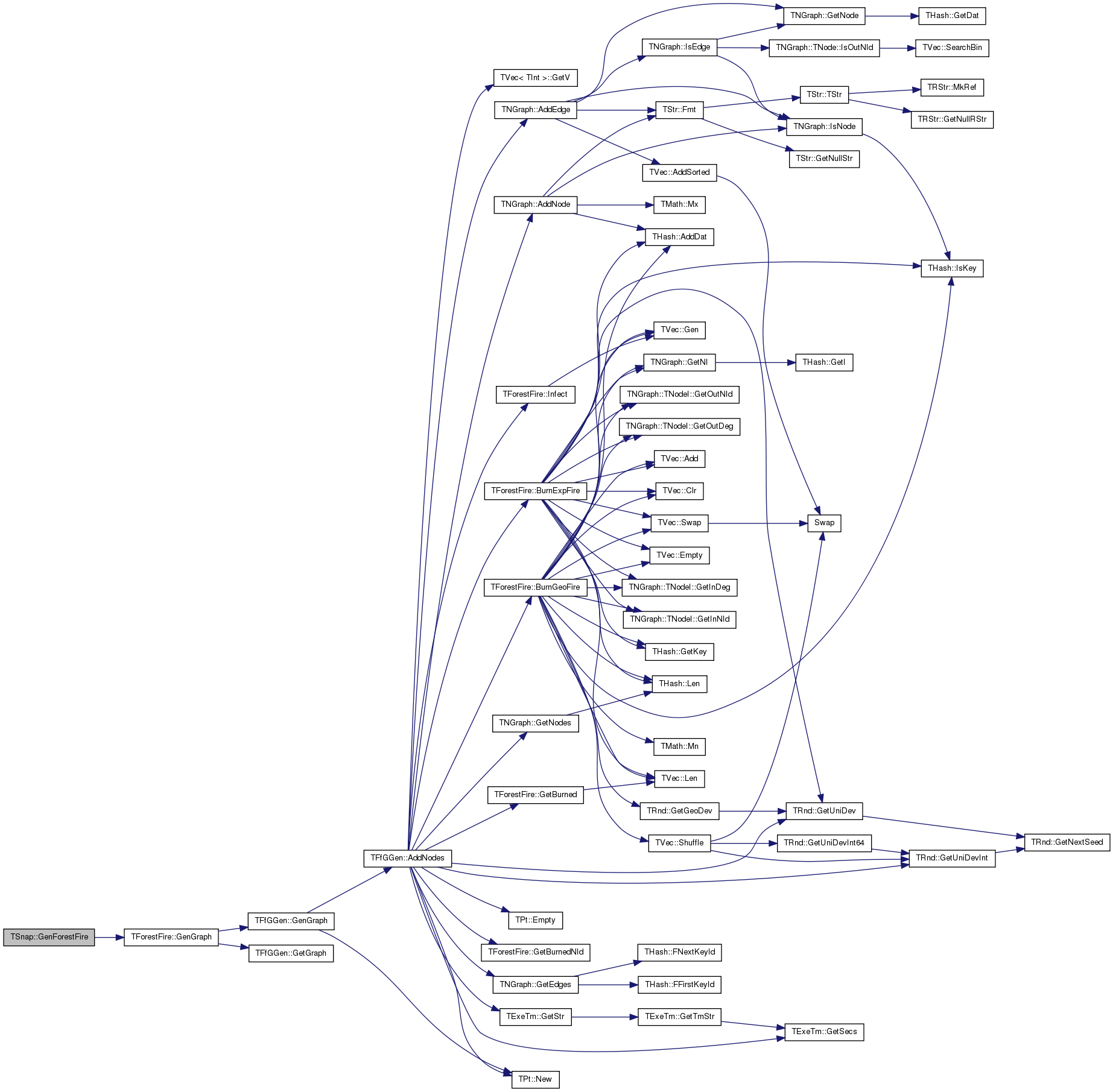
PGraph TSnap::GenFull

(

const int &

Nodes

)

Generates a complete graph on Nodes nodes. Graph has no self-loops.

Definition at line 119 of file ggen.h.

                                 {
  PGraph Graph = PGraph::TObj::New();
  Graph->Reserve(Nodes, Nodes*Nodes);
  for (int n = 0; n < Nodes; n++) {
    Graph->AddNode(n); }
  for (int n1 = 0; n1 < Nodes; n1++) {
    for (int n2 = 0; n2 < Nodes; n2++) {
      if (n1 != n2) { Graph->AddEdge(n1, n2); }
    }
  }
  return Graph;
}

PUNGraph TSnap::GenGeoPrefAttach	(	const int &	Nodes,
		const int &	OutDeg,
		const double &	Beta,
		TRnd &	Rnd
	)

Generates a random scale-free graph using the Geometric Preferential model.

Generates a random scale-free graph using the Geometric Preferential Attachment model by Flexman, Frieze and Vera. See: A geometric preferential attachment model of networks by Flexman, Frieze and Vera. WAW 2004. URL: http://math.cmu.edu/~af1p/Texfiles/GeoWeb.pdf

Definition at line 361 of file ggen.cpp.

References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Clr(), TVec< TVal, TSizeTy >::Del(), TSnap::TSnapDetail::GetSphereDev(), TRnd::GetUniDevInt(), TVec< TVal, TSizeTy >::Last(), TVec< TVal, TSizeTy >::Len(), TUNGraph::New(), TMath::Pi, TMath::Sqr(), TTriple< TVal1, TVal2, TVal3 >::Val1, TTriple< TVal1, TVal2, TVal3 >::Val2, and TTriple< TVal1, TVal2, TVal3 >::Val3.

                                                                                              {
  PUNGraph G = TUNGraph::New(Nodes, Nodes*OutDeg);
  TFltTrV PointV(Nodes, 0);
  TFltV ValV;
  // points on a sphere of radius 1/(2*pi)
  const double Rad = 0.5 * TMath::Pi;
  for (int i = 0; i < Nodes; i++) {
    TSnapDetail::GetSphereDev(3, Rnd, ValV);
    PointV.Add(TFltTr(Rad*ValV[0], Rad*ValV[1], Rad*ValV[2]));
  }
  const double R2 = TMath::Sqr(log((double) Nodes) / (pow((double) Nodes, 0.5-Beta)));
  TIntV DegV, NIdV;
  int SumDeg;
  for (int t = 0; t < Nodes; t++) {
    const int pid = t;
    const TFltTr& P1 = PointV[pid];
    // add node
    if (! G->IsNode(pid)) { G->AddNode(pid); }
    // find neighborhood
    DegV.Clr(false);  NIdV.Clr(false);  SumDeg=0;
    for (int p = 0; p < t; p++) {
      const TFltTr& P2 = PointV[p];
      if (TMath::Sqr(P1.Val1-P2.Val1)+TMath::Sqr(P1.Val2-P2.Val2)+TMath::Sqr(P1.Val3-P2.Val3) < R2) {
        NIdV.Add(p);
        DegV.Add(G->GetNI(p).GetDeg()+1);
        SumDeg += DegV.Last();
      }
    }
    // add edges
    for (int m = 0; m < OutDeg; m++) {
      const int rnd = Rnd.GetUniDevInt(SumDeg);
      int sum = 0, dst = -1;
      for (int s = 0; s < DegV.Len(); s++) {
        sum += DegV[s];
        if (rnd < sum) { dst=s;  break; }
      }
      if (dst != -1) {
        G->AddEdge(pid, NIdV[dst]);
        SumDeg -= DegV[dst];
        NIdV.Del(dst);  DegV.Del(dst);
      }
    }
  }
  return G;
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::GenGrid	(	const int &	Rows,
		const int &	Cols,
		const bool &	IsDir = true
	)

Generates a 2D-grid graph of Rows rows and Cols columns.

Definition at line 65 of file ggen.h.

References gfDirected.

                                                                    {
  PGraph GraphPt = PGraph::New();
  typename PGraph::TObj& Graph = *GraphPt;
  Graph.Reserve(Rows*Cols, 4*Rows*Cols);
  int node, r, c;
  for (node = 0; node < Rows * Cols; node++) {
    Graph.AddNode(node); }
  for (r = 0; r < Rows; r++) {
    for (c = 0; c < Cols; c++) {
      const int nodeId = Cols*r + c;
      if (r < Rows-1) { // bottom node
        Graph.AddEdge(nodeId, nodeId+Cols); 
        if (Graph.HasFlag(gfDirected) && ! IsDir) { 
          Graph.AddEdge(nodeId+Cols, nodeId); }
      }
      if (c < Cols-1) { // right node
        Graph.AddEdge(nodeId, nodeId+1); 
        if (Graph.HasFlag(gfDirected) && ! IsDir) { 
          Graph.AddEdge(nodeId+1, nodeId); }
      }
    }
  }
  return GraphPt;
}

PUNGraph TSnap::GenPrefAttach	(	const int &	Nodes,
		const int &	NodeOutDeg,
		TRnd &	Rnd
	)

Generates a power-law degree distribution using Barabasi-Albert model of scale-free graphs.

Barabasi-Albert model of scale-free graphs. The graph has power-law degree distribution. See: Emergence of scaling in random networks by Barabasi and Albert. URL: http://arxiv.org/abs/cond-mat/9910332

Definition at line 310 of file ggen.cpp.

References TVec< TVal, TSizeTy >::Add(), TUNGraph::AddEdge(), THashSet< TKey, THashFunc >::AddKey(), TUNGraph::AddNode(), THashSet< TKey, THashFunc >::Clr(), TVec< TVal, TSizeTy >::Len(), THashSet< TKey, THashFunc >::Len(), TPt< TUNGraph >::New(), TUNGraph::Reserve(), and TInt::Rnd.

                                                                           {
  PUNGraph GraphPt = PUNGraph::New();
  TUNGraph& Graph = *GraphPt;
  Graph.Reserve(Nodes, NodeOutDeg*Nodes);
  TIntV NIdV(NodeOutDeg*Nodes, 0);
  // first edge
  Graph.AddNode(0);  Graph.AddNode(1);
  NIdV.Add(0);  NIdV.Add(1);
  Graph.AddEdge(0, 1);
  TIntSet NodeSet;
  for (int node = 2; node < Nodes; node++) {
    NodeSet.Clr(false);
    while (NodeSet.Len() < NodeOutDeg && NodeSet.Len() < node) {
      NodeSet.AddKey(NIdV[TInt::Rnd.GetUniDevInt(NIdV.Len())]);
    }
    const int N = Graph.AddNode();
    for (int i = 0; i < NodeSet.Len(); i++) {
      Graph.AddEdge(N, NodeSet[i]);
      NIdV.Add(N);
      NIdV.Add(NodeSet[i]);
    }
  }
  return GraphPt;
}

Here is the call graph for this function:

PUNGraph TSnap::GenRewire	(	const PUNGraph &	OrigGraph,
		const int &	NSwitch,
		TRnd &	Rnd
	)

Rewire a random undirected graph. Keeps node degrees the same, but randomly rewires the edges.

Rewire the network. Keeps node degrees as is but randomly rewires the edges. Use this function to generate a random graph with the same degree sequence as the OrigGraph. See: On the uniform generation of random graphs with prescribed degree sequences by R. Milo, N. Kashtan, S. Itzkovitz, M. E. J. Newman, U. Alon URL: http://arxiv.org/abs/cond-mat/0312028

Definition at line 165 of file ggen.cpp.

References TUNGraph::AddEdge(), THashSet< TKey, THashFunc >::AddKey(), TUNGraph::AddNode(), THashSet< TKey, THashFunc >::DelKeyId(), THashSet< TKey, THashFunc >::GetRndKeyId(), TExeTm::GetSecs(), TExeTm::GetStr(), THashSet< TKey, THashFunc >::IsKey(), THashSet< TKey, THashFunc >::Len(), TUNGraph::New(), TUNGraph::Reserve(), Swap(), TPair< TVal1, TVal2 >::Val1, and TPair< TVal1, TVal2 >::Val2.

Referenced by GenRndDegK(), GenRndPowerLaw(), and TLocClust::PlotNCP().

                                                                             {
  const int Nodes = OrigGraph->GetNodes();
  const int Edges = OrigGraph->GetEdges();
  PUNGraph GraphPt = TUNGraph::New();
  TUNGraph& Graph = *GraphPt;
  Graph.Reserve(Nodes, -1);
  TExeTm ExeTm;
  // generate a graph that satisfies the constraints
  printf("Randomizing edges (%d, %d)...\n", Nodes, Edges);
  TIntPrSet EdgeSet(Edges);
  for (TUNGraph::TNodeI NI = OrigGraph->BegNI(); NI < OrigGraph->EndNI(); NI++) {
    const int NId = NI.GetId();
    for (int e = 0; e < NI.GetOutDeg(); e++) {
      if (NId <= NI.GetOutNId(e)) { continue; }
      EdgeSet.AddKey(TIntPr(NId, NI.GetOutNId(e)));
    }
    Graph.AddNode(NI.GetId());
  }
  // edge switching
  uint skip=0;
  for (uint swps = 0; swps < 2*uint(Edges)*uint(NSwitch); swps++) {
    const int keyId1 = EdgeSet.GetRndKeyId(Rnd);
    const int keyId2 = EdgeSet.GetRndKeyId(Rnd);
    if (keyId1 == keyId2) { skip++; continue; }
    const TIntPr& E1 = EdgeSet[keyId1];
    const TIntPr& E2 = EdgeSet[keyId2];
    TIntPr NewE1(E1.Val1, E2.Val1), NewE2(E1.Val2, E2.Val2);
    if (NewE1.Val1 > NewE1.Val2) { Swap(NewE1.Val1, NewE1.Val2); }
    if (NewE2.Val1 > NewE2.Val2) { Swap(NewE2.Val1, NewE2.Val2); }
    if (NewE1!=NewE2 && NewE1.Val1!=NewE1.Val2 && NewE2.Val1!=NewE2.Val2 && ! EdgeSet.IsKey(NewE1) && ! EdgeSet.IsKey(NewE2)) {
      EdgeSet.DelKeyId(keyId1);  EdgeSet.DelKeyId(keyId2);
      EdgeSet.AddKey(TIntPr(NewE1));
      EdgeSet.AddKey(TIntPr(NewE2));
    } else { skip++; }
    if (swps % Edges == 0) {
      printf("\r  %uk/%uk: %uk skip [%s]", swps/1000u, 2*uint(Edges)*uint(NSwitch)/1000u, skip/1000u, ExeTm.GetStr());
      if (ExeTm.GetSecs() > 2*3600) { printf(" *** Time limit!\n"); break; } // time limit 2 hours
    }
  }
  printf("\r  total %uk switchings attempted, %uk skiped  [%s]\n", 2*uint(Edges)*uint(NSwitch)/1000u, skip/1000u, ExeTm.GetStr());
  for (int e = 0; e < EdgeSet.Len(); e++) {
    Graph.AddEdge(EdgeSet[e].Val1, EdgeSet[e].Val2); }
  return GraphPt;
}

Here is the call graph for this function:

Here is the caller graph for this function:

PNGraph TSnap::GenRewire	(	const PNGraph &	OrigGraph,
		const int &	NSwitch,
		TRnd &	Rnd
	)

Rewire a random directed graph. Keeps node degrees the same, but randomly rewires the edges.

Rewire the network. Keeps node degrees as is but randomly rewires the edges. Use this function to generate a random graph with the same degree sequence as the OrigGraph. See: On the uniform generation of random graphs with prescribed degree sequences by R. Milo, N. Kashtan, S. Itzkovitz, M. E. J. Newman, U. Alon. URL: http://arxiv.org/abs/cond-mat/0312028

Definition at line 216 of file ggen.cpp.

References TNGraph::AddEdge(), THashSet< TKey, THashFunc >::AddKey(), TNGraph::AddNode(), TNGraph::BegNI(), THashSet< TKey, THashFunc >::DelKeyId(), TNGraph::EndNI(), TNGraph::GetEdges(), TNGraph::GetNodes(), THashSet< TKey, THashFunc >::GetRndKeyId(), TExeTm::GetSecs(), TExeTm::GetStr(), THashSet< TKey, THashFunc >::IsKey(), THashSet< TKey, THashFunc >::Len(), TNGraph::New(), TNGraph::Reserve(), TPair< TVal1, TVal2 >::Val1, and TPair< TVal1, TVal2 >::Val2.

                                                                           {
  const int Nodes = OrigGraph->GetNodes();
  const int Edges = OrigGraph->GetEdges();
  PNGraph GraphPt = TNGraph::New();
  TNGraph& Graph = *GraphPt;
  Graph.Reserve(Nodes, -1);
  TExeTm ExeTm;
  // generate a graph that satisfies the constraints
  printf("Randomizing edges (%d, %d)...\n", Nodes, Edges);
  TIntPrSet EdgeSet(Edges);
  for (TNGraph::TNodeI NI = OrigGraph->BegNI(); NI < OrigGraph->EndNI(); NI++) {
    const int NId = NI.GetId();
    for (int e = 0; e < NI.GetOutDeg(); e++) {
      EdgeSet.AddKey(TIntPr(NId, NI.GetOutNId(e))); }
    Graph.AddNode(NI);
  }
  // edge switching
  uint skip=0;
  for (uint swps = 0; swps < 2*uint(Edges)*uint(NSwitch); swps++) {
    const int keyId1 = EdgeSet.GetRndKeyId(Rnd);
    const int keyId2 = EdgeSet.GetRndKeyId(Rnd);
    if (keyId1 == keyId2) { skip++; continue; }
    const TIntPr& E1 = EdgeSet[keyId1];
    const TIntPr& E2 = EdgeSet[keyId2];
    TIntPr NewE1(E1.Val1, E2.Val1), NewE2(E1.Val2, E2.Val2);
    if (NewE1.Val1!=NewE2.Val1 && NewE1.Val2!=NewE2.Val1 && NewE1.Val2!=NewE2.Val1 && NewE1.Val2!=NewE2.Val2 && ! EdgeSet.IsKey(NewE1) && ! EdgeSet.IsKey(NewE2)) {
      EdgeSet.DelKeyId(keyId1);  EdgeSet.DelKeyId(keyId2);
      EdgeSet.AddKey(TIntPr(NewE1));
      EdgeSet.AddKey(TIntPr(NewE2));
    } else { skip++; }
    if (swps % Edges == 0) {
      printf("\r  %uk/%uk: %uk skip [%s]", swps/1000u, 2*uint(Edges)*uint(NSwitch)/1000u, skip/1000u, ExeTm.GetStr());
      if (ExeTm.GetSecs() > 2*3600) { printf(" *** Time limit!\n"); break; } // time limit 2 hours
    }
  }
  printf("\r  total %uk switchings attempted, %uk skiped  [%s]\n", 2*uint(Edges)*uint(NSwitch)/1000u, skip/1000u, ExeTm.GetStr());
  for (int e = 0; e < EdgeSet.Len(); e++) {
    Graph.AddEdge(EdgeSet[e].Val1, EdgeSet[e].Val2); }
  return GraphPt;
}

Here is the call graph for this function:

PBPGraph TSnap::GenRewire	(	const PBPGraph &	OrigGraph,
		const int &	NSwitch,
		TRnd &	Rnd
	)

Rewire a random bipartite graph. Keeps node degrees the same, but randomly rewires the edges.

Rewire a bipartite graph. Keeps node degrees as is but randomly rewires the edges. Use this function to generate a random graph with the same degree sequence as the OrigGraph. See: On the uniform generation of random graphs with prescribed degree sequences by R. Milo, N. Kashtan, S. Itzkovitz, M. E. J. Newman, U. Alon URL: http://arxiv.org/abs/cond-mat/0312028

Definition at line 263 of file ggen.cpp.

References TBPGraph::AddEdge(), THashSet< TKey, THashFunc >::AddKey(), TBPGraph::AddNode(), THashSet< TKey, THashFunc >::DelKeyId(), THashSet< TKey, THashFunc >::GetRndKeyId(), TExeTm::GetSecs(), TExeTm::GetStr(), IAssert, THashSet< TKey, THashFunc >::IsKey(), THashSet< TKey, THashFunc >::Len(), TBPGraph::New(), TBPGraph::Reserve(), TPair< TVal1, TVal2 >::Val1, and TPair< TVal1, TVal2 >::Val2.

                                                                             {
  const int Nodes = OrigGraph->GetNodes();
  const int Edges = OrigGraph->GetEdges();
  PBPGraph GraphPt = TBPGraph::New();
  TBPGraph& Graph = *GraphPt;
  Graph.Reserve(Nodes, -1);
  TExeTm ExeTm;
  // generate a graph that satisfies the constraints
  printf("Randomizing edges (%d, %d)...\n", Nodes, Edges);
  TIntPrSet EdgeSet(Edges);
  for (TBPGraph::TNodeI NI = OrigGraph->BegLNI(); NI < OrigGraph->EndLNI(); NI++) {
    const int NId = NI.GetId();
    for (int e = 0; e < NI.GetOutDeg(); e++) {
      EdgeSet.AddKey(TIntPr(NId, NI.GetOutNId(e))); } // edges left-->right
    Graph.AddNode(NI.GetId(), true); } // left nodes
  for (TBPGraph::TNodeI NI = OrigGraph->BegRNI(); NI < OrigGraph->EndRNI(); NI++) {
    Graph.AddNode(NI.GetId(), false); } // right nodes
  IAssert(EdgeSet.Len() == Edges);
  // edge switching
  uint skip=0;
  for (uint swps = 0; swps < 2*uint(Edges)*uint(NSwitch); swps++) {
    const int keyId1 = EdgeSet.GetRndKeyId(Rnd);
    const int keyId2 = EdgeSet.GetRndKeyId(Rnd);
    if (keyId1 == keyId2) { skip++; continue; }
    const TIntPr& E1 = EdgeSet[keyId1];
    const TIntPr& E2 = EdgeSet[keyId2];
    TIntPr NewE1(E1.Val1, E2.Val2), NewE2(E2.Val1, E1.Val2);
    if (NewE1!=NewE2 && NewE1.Val1!=NewE1.Val2 && NewE2.Val1!=NewE2.Val2 && ! EdgeSet.IsKey(NewE1) && ! EdgeSet.IsKey(NewE2)) {
      EdgeSet.DelKeyId(keyId1);  EdgeSet.DelKeyId(keyId2);
      EdgeSet.AddKey(TIntPr(NewE1));
      EdgeSet.AddKey(TIntPr(NewE2));
    } else { skip++; }
    if (swps % Edges == 0) {
      printf("\r  %uk/%uk: %uk skip [%s]", swps/1000u, 2*uint(Edges)*uint(NSwitch)/1000u, skip/1000u, ExeTm.GetStr());
      if (ExeTm.GetSecs() > 2*3600) { printf(" *** Time limit!\n"); break; } // time limit 2 hours
    }
  }
  printf("\r  total %uk switchings attempted, %uk skiped  [%s]\n", 2*uint(Edges)*uint(NSwitch)/1000u, skip/1000u, ExeTm.GetStr());
  for (int e = 0; e < EdgeSet.Len(); e++) {
    Graph.AddEdge(EdgeSet[e].Val1, EdgeSet[e].Val2); }
  return GraphPt;
}

Here is the call graph for this function:

PNGraph TSnap::GenRMat	(	const int &	Nodes,
		const int &	Edges,
		const double &	A,
		const double &	B,
		const double &	C,
		TRnd &	Rnd
	)

Generates a R-MAT graph using recursive descent into a 2x2 matrix [A,B; C, 1-(A+B+C)].

R-MAT Generator. The modes is based on the recursive descent into a 2x2 matrix [A,B; C, 1-(A+B+C)]. See: R-MAT Generator: A Recursive Model for Graph Mining. D. Chakrabarti, Y. Zhan and C. Faloutsos, in SIAM Data Mining 2004. URL: http://www.cs.cmu.edu/~deepay/mywww/papers/siam04.pdf

Definition at line 478 of file ggen.cpp.

References TVec< TVal, TSizeTy >::Add(), TNGraph::AddEdge(), TNGraph::AddNode(), TNGraph::Defrag(), Fail, TRnd::GetUniDev(), IAssert, TNGraph::IsEdge(), TNGraph::New(), and TNGraph::Reserve().

Referenced by GenRMatEpinions().

                                                                                                                  {
  PNGraph GraphPt = TNGraph::New();
  TNGraph& Graph = *GraphPt;
  Graph.Reserve(Nodes, Edges);
  IAssert(A+B+C < 1.0);
  int rngX, rngY, offX, offY;
  int Depth=0, Collisions=0, Cnt=0, PctDone=0;
  const int EdgeGap = Edges / 100 + 1;
  // sum of parameters (probabilities)
  TVec<double> sumA(128, 0), sumAB(128, 0), sumAC(128, 0), sumABC(128, 0);  // up to 2^128 vertices ~ 3.4e38
  for (int i = 0; i < 128; i++) {
    const double a = A * (Rnd.GetUniDev() + 0.5);
    const double b = B * (Rnd.GetUniDev() + 0.5);
    const double c = C * (Rnd.GetUniDev() + 0.5);
    const double d = (1.0 - (A+B+C)) * (Rnd.GetUniDev() + 0.5);
    const double abcd = a+b+c+d;
    sumA.Add(a / abcd);
    sumAB.Add((a+b) / abcd);
    sumAC.Add((a+c) / abcd);
    sumABC.Add((a+b+c) / abcd);
  }
  // nodes
  for (int node = 0; node < Nodes; node++) {
    IAssert(Graph.AddNode(-1) == node);
  }
  // edges
  for (int edge = 0; edge < Edges; ) {
    rngX = Nodes;  rngY = Nodes;  offX = 0;  offY = 0;
    Depth = 0;
    // recurse the matrix
    while (rngX > 1 || rngY > 1) {
      const double RndProb = Rnd.GetUniDev();
      if (rngX>1 && rngY>1) {
        if (RndProb < sumA[Depth]) { rngX/=2; rngY/=2; }
        else if (RndProb < sumAB[Depth]) { offX+=rngX/2;  rngX-=rngX/2;  rngY/=2; }
        else if (RndProb < sumABC[Depth]) { offY+=rngY/2;  rngX/=2;  rngY-=rngY/2; }
        else { offX+=rngX/2;  offY+=rngY/2;  rngX-=rngX/2;  rngY-=rngY/2; }
      } else
      if (rngX>1) { // row vector
        if (RndProb < sumAC[Depth]) { rngX/=2; rngY/=2; }
        else { offX+=rngX/2;  rngX-=rngX/2;  rngY/=2; }
      } else
      if (rngY>1) { // column vector
        if (RndProb < sumAB[Depth]) { rngX/=2; rngY/=2; }
        else { offY+=rngY/2;  rngX/=2;  rngY-=rngY/2; }
      } else { Fail; }
      Depth++;
    }
    // add edge
    const int NId1 = offX;
    const int NId2 = offY;
    if (NId1 != NId2 && ! Graph.IsEdge(NId1, NId2)) {
      Graph.AddEdge(NId1, NId2);
      if (++Cnt > EdgeGap) {
        Cnt=0;  printf("\r  %d%% edges", ++PctDone); }
      edge++;
    } else {
      Collisions++; }
  }
  printf("\r  RMat: nodes:%d, edges:%d, Iterations:%d, Collisions:%d (%.1f%%).\n", Nodes, Edges,
    Edges+Collisions, Collisions, 100*Collisions/double(Edges+Collisions));
  Graph.Defrag();
  return GraphPt;
}

Here is the call graph for this function:

Here is the caller graph for this function:

PNGraph TSnap::GenRMatEpinions

(

)

Generates a R-Mat graph, with a synthetic copy of the Epinions social network.

R-Mat generator with parameters set so that it generates a synthetic copy of the Epinions social network. The original Epinions social network can be downloaded at http://snap.stanford.edu/data/soc-Epinions1.html

Definition at line 547 of file ggen.cpp.

References GenRMat().

                          {
  return GenRMat(75888, 508837, 0.550, 0.228, 0.212);
}

Here is the call graph for this function:

PBPGraph TSnap::GenRndBipart	(	const int &	LeftNodes,
		const int &	RightNodes,
		const int &	Edges,
		TRnd &	Rnd
	)

Generates a random bipartite graph.

Definition at line 5 of file ggen.cpp.

References TRnd::GetUniDevInt(), IAssertR, and TBPGraph::New().

                                                                                                {
  PBPGraph G = TBPGraph::New();
  for (int i = 0; i < LeftNodes; i++) { G->AddNode(i, true); }
  for (int i = 0; i < RightNodes; i++) { G->AddNode(LeftNodes+i, false); }
  IAssertR(Edges <= LeftNodes*RightNodes, "Too many edges in the bipartite graph!");
  for (int edges = 0; edges < Edges; ) {
    const int LNId = Rnd.GetUniDevInt(LeftNodes);
    const int RNId = LeftNodes + Rnd.GetUniDevInt(RightNodes);
    if (G->AddEdge(LNId, RNId) != -2) { edges++; } // is new edge
  }
  return G;
}

Here is the call graph for this function:

PUNGraph TSnap::GenRndDegK	(	const int &	Nodes,
		const int &	NodeDeg,
		const int &	NSwitch,
		TRnd &	Rnd
	)

Generates a random graph where each node has degree exactly NodeDeg.

Definition at line 18 of file ggen.cpp.

References TVec< TVal, TSizeTy >::Add(), GenDegSeq(), GenRewire(), and IAssert.

                                                                                         {
  // create degree sequence
  TIntV DegV(Nodes, 0);
  int DegSum=0;
  for (int i = 0; i < Nodes; i++) {
    DegV.Add(NodeDeg);
    DegSum += NodeDeg;
  }
  IAssert(DegSum % 2 == 0);
  PUNGraph G = GenDegSeq(DegV, Rnd); // get some graph that obeys the degree sequnce
  return GenRewire(G, NSwitch, Rnd);  // make it random
}

Here is the call graph for this function:

template<class PGraph >

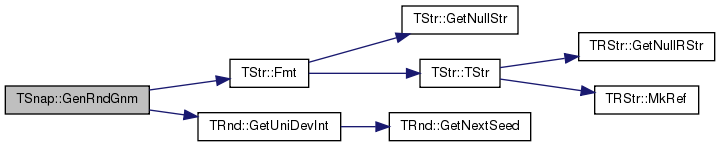
PGraph TSnap::GenRndGnm	(	const int &	Nodes,
		const int &	Edges,
		const bool &	IsDir = true,
		TRnd &	Rnd = TInt::Rnd
	)

Generates an Erdos-Renyi random graph.

Definition at line 218 of file ggen.h.

References TStr::Fmt(), TRnd::GetUniDevInt(), IAssert, and IAssertR.

                                                                                   {
  PGraph GraphPt = PGraph::New();
  typename PGraph::TObj& Graph = *GraphPt;
  Graph.Reserve(Nodes, Edges);
  IAssertR((1.0 * (Nodes-1) / 2 * (IsDir ? 2 : 1)) >= (1.0 * Edges / Nodes), TStr::Fmt("Not enough nodes (%d), for edges (%d).", Nodes, Edges));
  for (int node = 0; node < Nodes; node++) {
    IAssert(Graph.AddNode(node) == node);
  }
  for (int edge = 0; edge < Edges; ) {
    const int SrcNId = Rnd.GetUniDevInt(Nodes);
    const int DstNId = Rnd.GetUniDevInt(Nodes);
    if (SrcNId != DstNId && Graph.AddEdge(SrcNId, DstNId) != -2) { // is new edge
      if (! IsDir) { Graph.AddEdge(DstNId, SrcNId); }
      edge++;
    }
  }
  return GraphPt;
}

Here is the call graph for this function:

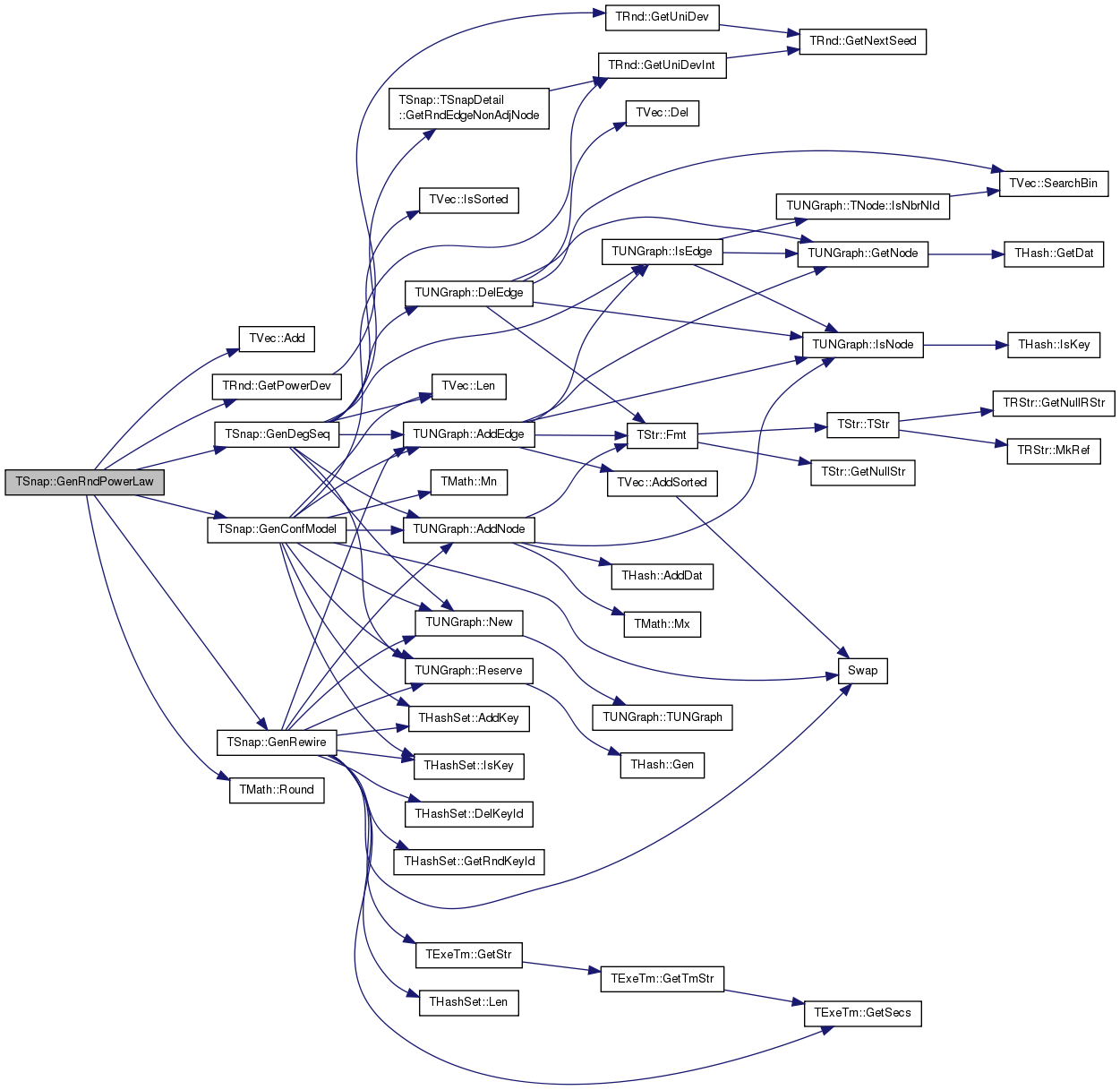
PUNGraph TSnap::GenRndPowerLaw	(	const int &	Nodes,
		const double &	PowerExp,
		const bool &	ConfModel,
		TRnd &	Rnd
	)

Generates a random scale-free graph with power-law degree distribution.

Generates a random scale-free graph with power-law degree distribution with exponent PowerExp. The method uses either the Configuration model (fast but the result is approximate) or the Edge Rewiring method (slow but exact).

Definition at line 34 of file ggen.cpp.

References TVec< TVal, TSizeTy >::Add(), GenConfModel(), GenDegSeq(), GenRewire(), TRnd::GetPowerDev(), and TMath::Round().

                                                                                                    {
  TIntV DegSeqV;
  uint DegSum=0;
  for (int n = 0; n < Nodes; n++) {
    const int Val = (int) TMath::Round(Rnd.GetPowerDev(PowerExp));
    if (! (Val >= 1 && Val < Nodes/2)) { n--; continue; } // skip nodes with too large degree
    DegSeqV.Add(Val);
    DegSum += Val;
  }
  printf("%d nodes, %u edges\n", Nodes, DegSum);
  if (DegSum % 2 == 1) { DegSeqV[0] += 1; }
  if (ConfModel) {
    // use configuration model -- fast but does not exactly obey the degree sequence
    return GenConfModel(DegSeqV, Rnd);
  } else {
    PUNGraph G = TSnap::GenDegSeq(DegSeqV, Rnd);
    return TSnap::GenRewire(G, 10, Rnd);
  }
}

Here is the call graph for this function:

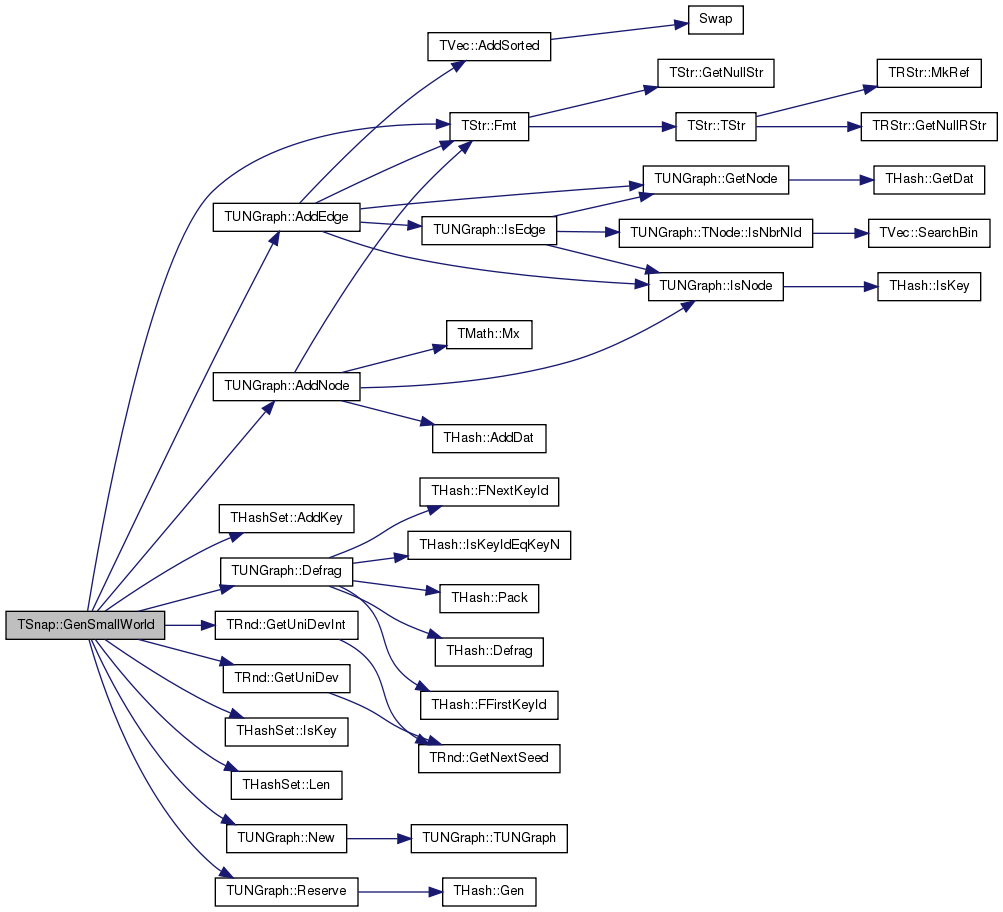
PUNGraph TSnap::GenSmallWorld	(	const int &	Nodes,
		const int &	NodeOutDeg,
		const double &	RewireProb,
		TRnd &	Rnd
	)

Generates a randomly small-world graph using the Watts-Strogatz model.

Generates a small-world graph using the Watts-Strogatz model. We assume a circle where each node creates links to NodeOutDeg other nodes. This way at the end each node is connected to 2*NodeOutDeg other nodes. See: Collective dynamics of 'small-world' networks. Watts and Strogatz. URL: http://research.yahoo.com/files/w_s_NATURE_0.pdf

Definition at line 412 of file ggen.cpp.

References TUNGraph::AddEdge(), THashSet< TKey, THashFunc >::AddKey(), TUNGraph::AddNode(), TUNGraph::Defrag(), TStr::Fmt(), TRnd::GetUniDev(), TRnd::GetUniDevInt(), IAssert, IAssertR, THashSet< TKey, THashFunc >::IsKey(), THashSet< TKey, THashFunc >::Len(), TUNGraph::New(), and TUNGraph::Reserve().

                                                                                                     {
  THashSet<TIntPr> EdgeSet(Nodes*NodeOutDeg);
  
  IAssertR(Nodes > NodeOutDeg, TStr::Fmt("Insufficient nodes for out degree, %d!", NodeOutDeg));
  for (int node = 0; node < Nodes; node++) {
    const int src = node;
    for (int edge = 1; edge <= NodeOutDeg; edge++) {
      int dst = (node+edge) % Nodes;      // edge to next neighbor
      if (Rnd.GetUniDev() < RewireProb) { // random edge
        dst = Rnd.GetUniDevInt(Nodes);
        while (dst == src || EdgeSet.IsKey(TIntPr(src, dst))) {
          dst = Rnd.GetUniDevInt(Nodes); }
      }
      EdgeSet.AddKey(TIntPr(src, dst));
    }
  }
  PUNGraph GraphPt = TUNGraph::New();
  TUNGraph& Graph = *GraphPt;
  Graph.Reserve(Nodes, EdgeSet.Len());
  int node;
  for (node = 0; node < Nodes; node++) {
    IAssert(Graph.AddNode(node) == node);
  }
  for (int edge = 0; edge < EdgeSet.Len(); edge++) {
    Graph.AddEdge(EdgeSet[edge].Val1, EdgeSet[edge].Val2);
  }
  Graph.Defrag();
  return GraphPt;
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::GenStar	(	const int &	Nodes,
		const bool &	IsDir = true
	)

Generates a graph with star topology. Node id 0 is in the center and then links to all other nodes.

Definition at line 91 of file ggen.h.

References gfDirected.

                                                    {
  PGraph Graph = PGraph::TObj::New();
  Graph->Reserve(Nodes, Nodes);
  Graph->AddNode(0);
  for (int n = 1; n < Nodes; n++) {
    Graph->AddNode(n);
    Graph->AddEdge(0, n);
    if (Graph->HasFlag(gfDirected) && ! IsDir) { Graph->AddEdge(n, 0); }
  }
  return Graph;
}

template<class PGraph >

PGraph TSnap::GenTree	(	const int &	Fanout,
		const int &	Levels,
		const bool &	IsDir = true,
		const bool &	ChildPointsToParent = true
	)

Generates a tree graph of Levels levels with every parent having Fanout children.

Definition at line 133 of file ggen.h.

                                                                                                         {
  const int Nodes = (int) (pow(double(Fanout), double(Levels+1)) - 1) / (Fanout - 1);
  const int Edges = Nodes - 1;
  PGraph GraphPt = PGraph::New();
  typename PGraph::TObj& Graph = *GraphPt;
  Graph.Reserve(Nodes, Edges);
  int node;
  for (node = 0; node < Nodes; node++) {
    Graph.AddNode(node); }
  // non-leaf nodes
  for (node = 0; node < (int) Nodes - (int) pow(double(Fanout), double(Levels)); node++) {
    for (int edge = 1; edge <= Fanout; edge++) {
      if (IsDir) {
        if (ChildPointsToParent) { Graph.AddEdge(Fanout*node+edge, node); }
        else { Graph.AddEdge(node, Fanout*node+edge); }
      } else {
        Graph.AddEdge(node, Fanout*node+edge); // link children
        Graph.AddEdge(Fanout*node+edge, node);
      }
    }
  }
  return GraphPt;
}

void TSnap::Get1CnCom	(	const PUNGraph &	Graph,
		TCnComV &	Cn1ComV
	)

Returns 1-components: maximal connected components of that can be disconnected from the Graph by removing a single edge.

We find such components as follows: Find all bridge edges, remove them from the Graph, find largest component K and add back all bridges that do not touch K. Now, find the connected components of this graph.

Definition at line 98 of file cncom.cpp.

References THashSet< TKey, THashFunc >::AddKey(), TVec< TVal, TSizeTy >::Clr(), TVec< TVal, TSizeTy >::Del(), TVec< TVal, TSizeTy >::Empty(), GetEdgeBridges(), GetWccs(), IAssert, TVec< TVal, TSizeTy >::Len(), and TUNGraph::New().

Referenced by TLocClustStat::BagOfWhiskers(), TLocClustStat::BagOfWhiskers2(), and TLocClust::DrawWhiskers().

                                                        {
  //TCnCom::GetWccCnt(Graph, SzCntV);  IAssertR(SzCntV.Len() == 1, "Graph is not connected.");
  TIntPrV EdgeV;
  GetEdgeBridges(Graph, EdgeV);
  if (EdgeV.Empty()) { Cn1ComV.Clr(false); return; }
  PUNGraph TmpG = TUNGraph::New();
  *TmpG = *Graph;
  for (int e = 0; e < EdgeV.Len(); e++) {
    TmpG->DelEdge(EdgeV[e].Val1, EdgeV[e].Val2);  }
  TCnComV CnComV;  GetWccs(TmpG, CnComV);
  IAssert(CnComV.Len() >= 2);
  const TIntV& MxWcc = CnComV[0].NIdV;
  TIntSet MxCcSet(MxWcc.Len());
  for (int i = 0; i < MxWcc.Len(); i++) { 
    MxCcSet.AddKey(MxWcc[i]); }
  // create new graph: bridges not touching MxCc of G with no bridges
  for (int e = 0; e < EdgeV.Len(); e++) {
    if (! MxCcSet.IsKey(EdgeV[e].Val1) &&  ! MxCcSet.IsKey(EdgeV[e].Val2)) {
      TmpG->AddEdge(EdgeV[e].Val1, EdgeV[e].Val2); }
  }
  GetWccs(TmpG, Cn1ComV);
  // remove the largest component of G
  for (int c = 0; c < Cn1ComV.Len(); c++) {
    if (MxCcSet.IsKey(Cn1ComV[c].NIdV[0])) {
      Cn1ComV.Del(c);  break; }
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSnap::Get1CnComSzCnt	(	const PUNGraph &	Graph,
		TIntPrV &	SzCntV
	)

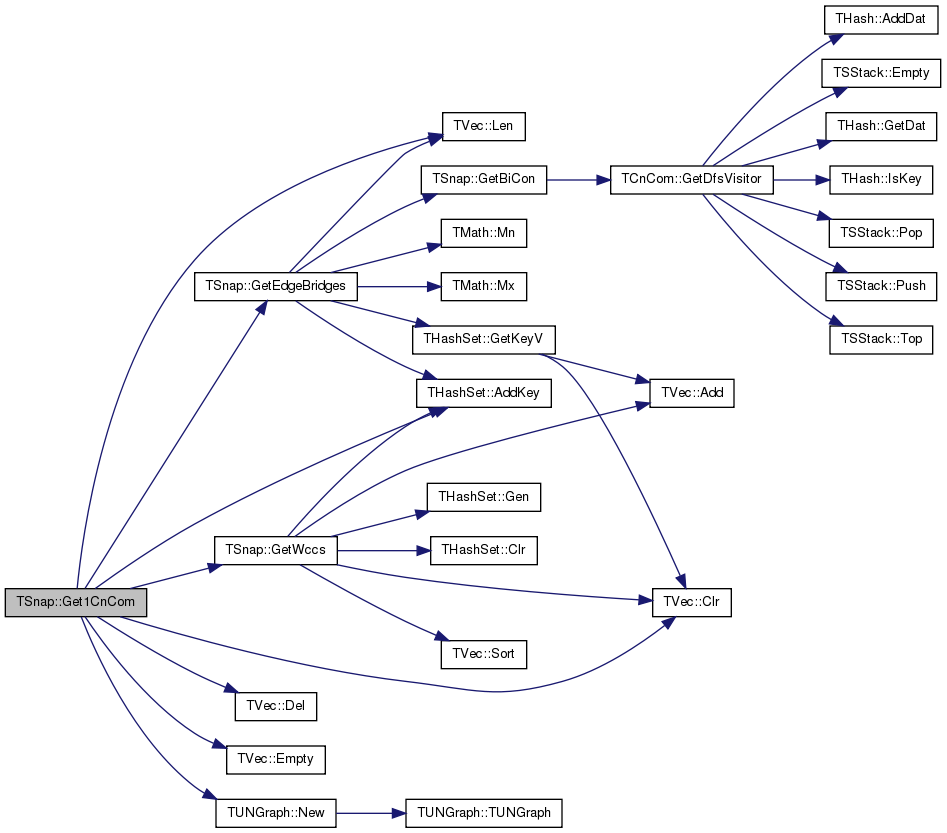
Distribution of sizes of 1-components, maximal number of components that can be disconnected from the Graph by removing a single edge.

We find such components as follows: Find all bridge edges, remove them from the Graph, find largest component K and add back all bridges that do not touch K. Now, find the connected components of this graph.

Definition at line 70 of file cncom.cpp.

References THashSet< TKey, THashFunc >::AddKey(), TVec< TVal, TSizeTy >::Clr(), TVec< TVal, TSizeTy >::Del(), TVec< TVal, TSizeTy >::Empty(), GetEdgeBridges(), GetWccs(), GetWccSzCnt(), IAssert, TVec< TVal, TSizeTy >::Len(), and TUNGraph::New().

                                                            {
  //TCnCom::GetWccCnt(Graph, SzCntV);  IAssertR(SzCntV.Len() == 1, "Graph is not connected.");
  TIntPrV EdgeV;
  GetEdgeBridges(Graph, EdgeV);
  if (EdgeV.Empty()) { SzCntV.Clr(false); return; }
  PUNGraph TmpG = TUNGraph::New();
  *TmpG = *Graph;
  for (int e = 0; e < EdgeV.Len(); e++) {
    TmpG->DelEdge(EdgeV[e].Val1, EdgeV[e].Val2);  }
  TCnComV CnComV;  GetWccs(TmpG, CnComV);
  IAssert(CnComV.Len() >= 2);
  const TIntV& MxWcc = CnComV[0].NIdV;
  TIntSet MxCcSet(MxWcc.Len());
  for (int i = 0; i < MxWcc.Len(); i++) { 
    MxCcSet.AddKey(MxWcc[i]); }
  // create new graph: bridges not touching MxCc of G with no bridges
  for (int e = 0; e < EdgeV.Len(); e++) {
    if (! MxCcSet.IsKey(EdgeV[e].Val1) &&  ! MxCcSet.IsKey(EdgeV[e].Val2)) {
      TmpG->AddEdge(EdgeV[e].Val1, EdgeV[e].Val2); }
  }
  GetWccSzCnt(TmpG, SzCntV);
  for (int c = 0; c < SzCntV.Len(); c++) {
    if (SzCntV[c].Val1 == MxCcSet.Len()) { 
      SzCntV.Del(c);  break; }
  }
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetAnf	(	const PGraph &	Graph,
		const int &	SrcNId,
		TIntFltKdV &	DistNbrsV,
		const int &	MxDist,
		const bool &	IsDir,
		const int &	NApprox = 32
	)

Approximate Neighborhood Function of a node: Returns the (approximate) number of nodes reachable from SrcNId in less than H hops.

Parameters

SrcNId	Starting node.
DistNbrsV	Maps between the distance H (in hops) and the number of nodes reachable in <=H hops.
MxDist	Maximum number of hops the algorithm spreads from SrcNId.
IsDir	false: consider links as undirected (drop link directions).
NApprox	Quality of approximation. See the ANF paper.

Definition at line 205 of file anf.h.

References TGraphAnf< PGraph >::GetNodeAnf().

Referenced by PlotHops(), and TGStat::TakeDiam().

                                                                                                                                     {
  TGraphAnf<PGraph> Anf(Graph, NApprox, 5, 0);
  Anf.GetNodeAnf(SrcNId, DistNbrsV, MxDist, IsDir);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::GetAnf	(	const PGraph &	Graph,
		TIntFltKdV &	DistNbrsV,
		const int &	MxDist,
		const bool &	IsDir,
		const int &	NApprox = 32
	)

Approximate Neighborhood Function of a Graph: Returns the number of pairs of nodes reachable in less than H hops. For example, DistNbrsV.GetDat(0) is the number of nodes in the graph, DistNbrsV.GetDat(1) is the number of nodes+edges and so on.

Parameters

DistNbrsV	Maps between the distance H (in hops) and the number of nodes reachable in <=H hops.
MxDist	Maximum number of hops the algorithm spreads from SrcNId.
IsDir	false: consider links as undirected (drop link directions).
NApprox	Quality of approximation. See the ANF paper.

Definition at line 211 of file anf.h.

References TGraphAnf< PGraph >::GetGraphAnf().

                                                                                                                  {
  TGraphAnf<PGraph> Anf(Graph, NApprox, 5, 0);
  Anf.GetGraphAnf(DistNbrsV, MxDist, IsDir);
}

Here is the call graph for this function:

template<class PGraph >

double TSnap::GetAnfEffDiam	(	const PGraph &	Graph,
		const bool &	IsDir,
		const double &	Percentile,
		const int &	NApprox
	)

Returns a given Percentile of the shortest path length distribution of a Graph (based on a single run of ANF of approximation quality NApprox).

Parameters

IsDir

false: consider links as undirected (drop link directions).

Definition at line 217 of file anf.h.

References TSnap::TSnapDetail::CalcEffDiam(), and TGraphAnf< PGraph >::GetGraphAnf().

Referenced by GetAnfEffDiam(), TKroneckerLL::GradDescentConvergence(), TTimeNet::PlotEffDiam(), and TTimeNENet::PlotEffDiam().

                                                                                                           {
  TIntFltKdV DistNbrsV;
  TGraphAnf<PGraph> Anf(Graph, NApprox, 5, 0);
  Anf.GetGraphAnf(DistNbrsV, -1, IsDir);
  return TSnap::TSnapDetail::CalcEffDiam(DistNbrsV, Percentile);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

double TSnap::GetAnfEffDiam	(	const PGraph &	Graph,
		const int	NRuns = 1,
		int	NApprox = -1
	)

Returns a 90-th percentile of the shortest path length distribution of a Graph (based on a NRuns runs of ANF of approximation quality NApprox).

Parameters

IsDir

false: consider links as undirected (drop link directions).

Definition at line 225 of file anf.h.

References TMom::Add(), TMom::Def(), GetAnfEffDiam(), and TMom::GetMean().

                                                                        {
  //return TSnap::GetEffDiam(Graph, IsDir, 0.9, 32);
  TMom Mom;
  if (NApprox == -1) {
    if (Graph->GetNodes() < 100000) { NApprox = 64; }
    else if (Graph->GetNodes() < 1000000) { NApprox = 32; }
    else { NApprox = 16; }
  }
  const bool IsDir = false;
  for (int r = 0; r < NRuns; r++) {
    Mom.Add(TSnap::GetAnfEffDiam(Graph, IsDir, 0.9, NApprox));
  }
  Mom.Def();
  return Mom.GetMean();
}

Here is the call graph for this function:

void TSnap::GetArtPoints	(	const PUNGraph &	Graph,
		TIntV &	ArtNIdV
	)

Returns articulation points of a Graph.

Articulation point (or a cut vertex) is any node that when removed increases the number of connected components.

Definition at line 48 of file cncom.cpp.

References TCnCom::GetDfsVisitor().

                                                         {
  TArtPointVisitor Visitor(Graph->GetNodes());
  TCnCom::GetDfsVisitor(Graph, Visitor);
  Visitor.ArtSet.GetKeyV(ArtNIdV);
}

Here is the call graph for this function:

void TSnap::GetBetweennessCentr	(	const PUNGraph &	Graph,
		const TIntV &	BtwNIdV,
		TIntFltH &	NodeBtwH,
		const bool &	DoNodeCent,
		TIntPrFltH &	EdgeBtwH,
		const bool &	DoEdgeCent
	)

Computes (approximate) Beetweenness Centrality of all nodes and all edges of the network. To obtain exact betweenness values one needs to solve single-source shortest-path problem for every node. To speed up the algorithm we solve the shortest-path problem for the BtwNIdV subset of nodes. This gives centrality values that are about Graph->GetNodes()/BtwNIdV.Len() times lower than the exact betweenness centrality valus. See "A Faster Algorithm for Beetweenness Centrality", Ulrik Brandes, Journal of Mathematical Sociology, 2001, and "Centrality Estimation in Large Networks", Urlik Brandes and Christian Pich, 2006 for more details.

Definition at line 28 of file centr.cpp.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), THash< TKey, TDat, THashFunc >::Clr(), TSStack< TVal >::Clr(), TQQueue< TVal >::Clr(), TSStack< TVal >::Empty(), TQQueue< TVal >::Empty(), THash< TKey, TDat, THashFunc >::GetDat(), TUNGraph::TNodeI::GetId(), TUNGraph::TNodeI::GetOutDeg(), TUNGraph::TNodeI::GetOutNId(), TVec< TVal, TSizeTy >::Len(), TMath::Mn(), TMath::Mx(), TSStack< TVal >::Pop(), TQQueue< TVal >::Pop(), TSStack< TVal >::Push(), TQQueue< TVal >::Push(), TSStack< TVal >::Top(), and TQQueue< TVal >::Top().

Referenced by TSnap::TSnapDetail::CmtyGirvanNewmanStep(), and GetBetweennessCentr().

                                                                                                                                                                {
  if (DoNodeCent) { NodeBtwH.Clr(); }
  if (DoEdgeCent) { EdgeBtwH.Clr(); }
  const int nodes = Graph->GetNodes();
  TIntS S(nodes);
  TIntQ Q(nodes);
  TIntIntVH P(nodes); // one vector for every node
  TIntFltH delta(nodes);
  TIntH sigma(nodes), d(nodes);
  // init
  for (TUNGraph::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (DoNodeCent) {
      NodeBtwH.AddDat(NI.GetId(), 0); }
    if (DoEdgeCent) {
      for (int e = 0; e < NI.GetOutDeg(); e++) {
        if (NI.GetId() < NI.GetOutNId(e)) {
          EdgeBtwH.AddDat(TIntPr(NI.GetId(), NI.GetOutNId(e)), 0); }
      }
    }
    sigma.AddDat(NI.GetId(), 0);
    d.AddDat(NI.GetId(), -1);
    P.AddDat(NI.GetId(), TIntV());
    delta.AddDat(NI.GetId(), 0);
  }
  // calc betweeness
  for (int k=0; k < BtwNIdV.Len(); k++) {
    const TUNGraph::TNodeI NI = Graph->GetNI(BtwNIdV[k]);
    // reset
    for (int i = 0; i < sigma.Len(); i++) {
      sigma[i]=0;  d[i]=-1;  delta[i]=0;  P[i].Clr(false);
    }
    S.Clr(false);
    Q.Clr(false);
    sigma.AddDat(NI.GetId(), 1);
    d.AddDat(NI.GetId(), 0);
    Q.Push(NI.GetId());
    while (! Q.Empty()) {
      const int v = Q.Top();  Q.Pop();
      const TUNGraph::TNodeI NI2 = Graph->GetNI(v);
      S.Push(v);
      const int VDat = d.GetDat(v);
      for (int e = 0; e < NI2.GetOutDeg(); e++) {
        const int w = NI2.GetOutNId(e);
        if (d.GetDat(w) < 0) { // find w for the first time
          Q.Push(w);
          d.AddDat(w, VDat+1);
        }
        //shortest path to w via v ?
        if (d.GetDat(w) == VDat+1) {
          sigma.AddDat(w) += sigma.GetDat(v);
          P.GetDat(w).Add(v);
        }
      }
    }
    while (! S.Empty()) {
      const int w = S.Top();
      const double SigmaW = sigma.GetDat(w);
      const double DeltaW = delta.GetDat(w);
      const TIntV NIdV = P.GetDat(w);
      S.Pop();
      for (int i = 0; i < NIdV.Len(); i++) {
        const int nid = NIdV[i];
        const double c = (sigma.GetDat(nid)*1.0/SigmaW) * (1+DeltaW);
        delta.AddDat(nid) += c;
        if (DoEdgeCent) {
          EdgeBtwH.AddDat(TIntPr(TMath::Mn(nid, w), TMath::Mx(nid, w))) += c; }
      }
      if (DoNodeCent && w != NI.GetId()) {
        NodeBtwH.AddDat(w) += delta.GetDat(w)/2.0; }
    }
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSnap::GetBetweennessCentr	(	const PUNGraph &	Graph,
		TIntFltH &	NIdBtwH,
		const double &	NodeFrac = 1.0
	)

Computes (approximate) Node Beetweenness Centrality based on a sample of NodeFrac nodes.

Parameters

NIdBtwH	hash table mapping node ids to their corresponding betweenness centrality values.
NodeFrac	quality of approximation. NodeFrac=1.0 gives exact betweenness values.

Definition at line 103 of file centr.cpp.

References TVec< TVal, TSizeTy >::DelLast(), GetBetweennessCentr(), TVec< TVal, TSizeTy >::Len(), TInt::Rnd, and TVec< TVal, TSizeTy >::Shuffle().

                                                                                            {
  TIntPrFltH EdgeBtwH;
  TIntV NIdV;  Graph->GetNIdV(NIdV);
  if (NodeFrac < 1.0) { // calculate beetweenness centrality for a subset of nodes
    NIdV.Shuffle(TInt::Rnd);
    for (int i = int((1.0-NodeFrac)*NIdV.Len()); i > 0; i--) {
      NIdV.DelLast(); }
  }
  GetBetweennessCentr(Graph, NIdV, NodeBtwH, true, EdgeBtwH, false);
}

Here is the call graph for this function:

void TSnap::GetBetweennessCentr	(	const PUNGraph &	Graph,
		TIntPrFltH &	EdgeBtwH,
		const double &	NodeFrac = 1.0
	)

Computes (approximate) Edge Beetweenness Centrality based on a sample of NodeFrac nodes.

Parameters

EdgeBtwH	hash table mapping edges (pairs of node ids) to their corresponding betweenness centrality values.
NodeFrac	quality of approximation. NodeFrac=1.0 gives exact betweenness values.

Definition at line 114 of file centr.cpp.

References TVec< TVal, TSizeTy >::DelLast(), GetBetweennessCentr(), TVec< TVal, TSizeTy >::Len(), TInt::Rnd, and TVec< TVal, TSizeTy >::Shuffle().

                                                                                              {
  TIntFltH NodeBtwH;
  TIntV NIdV;  Graph->GetNIdV(NIdV);
  if (NodeFrac < 1.0) { // calculate beetweenness centrality for a subset of nodes
    NIdV.Shuffle(TInt::Rnd);
    for (int i = int((1.0-NodeFrac)*NIdV.Len()); i > 0; i--) {
      NIdV.DelLast(); }
  }
  GetBetweennessCentr(Graph, NIdV, NodeBtwH, false, EdgeBtwH, true);
}

Here is the call graph for this function:

void TSnap::GetBetweennessCentr	(	const PUNGraph &	Graph,
		TIntFltH &	NIdBtwH,
		TIntPrFltH &	EdgeBtwH,
		const double &	NodeFrac = 1.0
	)

Computes (approximate) Node and Edge Beetweenness Centrality based on a sample of NodeFrac nodes.

Parameters

NIdBtwH	hash table mapping node ids to their corresponding betweenness centrality values.
EdgeBtwH	hash table mapping edges (pairs of node ids) to their corresponding betweenness centrality values.
NodeFrac	quality of approximation. NodeFrac=1.0 gives exact betweenness values.

Definition at line 125 of file centr.cpp.

References TVec< TVal, TSizeTy >::DelLast(), GetBetweennessCentr(), TVec< TVal, TSizeTy >::Len(), TInt::Rnd, and TVec< TVal, TSizeTy >::Shuffle().

                                                                                                                  {
  TIntV NIdV;  Graph->GetNIdV(NIdV);
  if (NodeFrac < 1.0) { // calculate beetweenness centrality for a subset of nodes
    NIdV.Shuffle(TInt::Rnd);
    for (int i = int((1.0-NodeFrac)*NIdV.Len()); i > 0; i--) {
      NIdV.DelLast(); }
  }
  GetBetweennessCentr(Graph, NIdV, NodeBtwH, true, EdgeBtwH, true);
}

Here is the call graph for this function:

template<class PGraph >

double TSnap::GetBfsEffDiam	(	const PGraph &	Graph,
		const int &	NTestNodes,
		const bool &	IsDir = false
	)

Returns the (approximation of the) Effective Diameter (90-th percentile of the distribution of shortest path lengths) of a graph (by performing BFS from NTestNodes random starting nodes).

Parameters

IsDir

false: ignore edge directions and consider edges/paths as undirected (in case they are directed).

Definition at line 278 of file bfsdfs.h.

Referenced by GetBfsEffDiam(), GetBfsFullDiam(), TTimeNet::PlotMissingPast(), and PrintInfo().

                                                                                    {
  int FullDiam;
  double EffDiam;
  GetBfsEffDiam(Graph, NTestNodes, IsDir, EffDiam, FullDiam);
  return EffDiam;
}

Here is the caller graph for this function:

template<class PGraph >

double TSnap::GetBfsEffDiam	(	const PGraph &	Graph,
		const int &	NTestNodes,
		const bool &	IsDir,
		double &	EffDiamX,
		int &	FullDiamX
	)

Returns the (approximation of the) Effective Diameter and the Diameter of a graph (by performing BFS from NTestNodes random starting nodes).

Parameters

IsDir

false: ignore edge directions and consider edges/paths as undirected (in case they are directed).

Definition at line 286 of file bfsdfs.h.

References GetBfsEffDiam().

                                                                                                                    {
  double AvgDiam;
  EffDiam = -1;  FullDiam = -1;
  return GetBfsEffDiam(Graph, NTestNodes, IsDir, EffDiam, FullDiam, AvgDiam);
}

Here is the call graph for this function:

template<class PGraph >

double TSnap::GetBfsEffDiam	(	const PGraph &	Graph,
		const int &	NTestNodes,
		const bool &	IsDir,
		double &	EffDiamX,
		int &	FullDiamX,
		double &	AvgSPLX
	)

Returns the (approximation of the) Effective Diameter, the Diameter and the Average Shortest Path length in a graph (by performing BFS from NTestNodes random starting nodes). GetBfsEffDiam3.

Definition at line 293 of file bfsdfs.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TSnap::TSnapDetail::CalcEffDiamPdf(), TBreathFS< PGraph >::DoBfs(), THash< TKey, TDat, THashFunc >::GetKey(), TVec< TVal, TSizeTy >::Last(), THash< TKey, TDat, THashFunc >::Len(), TMath::Mn(), TInt::Mx, TBreathFS< PGraph >::NIdDistH, TInt::Rnd, TVec< TVal, TSizeTy >::Shuffle(), and TVec< TVal, TSizeTy >::Sort().

                                                                                                                                    {
  EffDiam = -1;  FullDiam = -1;  AvgSPL = -1;
  TIntFltH DistToCntH;
  TBreathFS<PGraph> BFS(Graph);
  // shotest paths
  TIntV NodeIdV;
  Graph->GetNIdV(NodeIdV);  NodeIdV.Shuffle(TInt::Rnd);
  for (int tries = 0; tries < TMath::Mn(NTestNodes, Graph->GetNodes()); tries++) {
    const int NId = NodeIdV[tries];
    BFS.DoBfs(NId, true, ! IsDir, -1, TInt::Mx);
    for (int i = 0; i < BFS.NIdDistH.Len(); i++) {
      DistToCntH.AddDat(BFS.NIdDistH[i]) += 1; }
  }
  TIntFltKdV DistNbrsPdfV;
  double SumPathL=0, PathCnt=0;
  for (int i = 0; i < DistToCntH.Len(); i++) {
    DistNbrsPdfV.Add(TIntFltKd(DistToCntH.GetKey(i), DistToCntH[i]));
    SumPathL += DistToCntH.GetKey(i) * DistToCntH[i];
    PathCnt += DistToCntH[i];
  }
  DistNbrsPdfV.Sort();
  EffDiam = TSnap::TSnapDetail::CalcEffDiamPdf(DistNbrsPdfV, 0.9); // effective diameter (90-th percentile)
  FullDiam = DistNbrsPdfV.Last().Key;                // approximate full diameter (max shortest path length over the sampled nodes)
  AvgSPL = SumPathL/PathCnt;                        // average shortest path length
  return EffDiam;
}

Here is the call graph for this function:

template<class PGraph >

double TSnap::GetBfsEffDiam	(	const PGraph &	Graph,
		const int &	NTestNodes,
		const TIntV &	SubGraphNIdV,
		const bool &	IsDir,
		double &	EffDiamX,
		int &	FullDiamX
	)

Use the whole graph (all edges) to measure the shortest path lengths but only report the path lengths between nodes in the SubGraphNIdV. GetBfsEffDiam4.

Definition at line 321 of file bfsdfs.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TSnap::TSnapDetail::CalcEffDiamPdf(), TBreathFS< PGraph >::DoBfs(), THash< TKey, TDat, THashFunc >::GetKey(), THash< TKey, TDat, THashFunc >::IsKeyGetDat(), TVec< TVal, TSizeTy >::Last(), THash< TKey, TDat, THashFunc >::Len(), TVec< TVal, TSizeTy >::Len(), TMath::Mn(), TInt::Mx, TBreathFS< PGraph >::NIdDistH, TInt::Rnd, TVec< TVal, TSizeTy >::Shuffle(), and TVec< TVal, TSizeTy >::Sort().

                                                                                                                                               {
  EffDiam = -1;
  FullDiam = -1;

  TIntFltH DistToCntH;
  TBreathFS<PGraph> BFS(Graph);
  // shotest paths
  TIntV NodeIdV(SubGraphNIdV);  NodeIdV.Shuffle(TInt::Rnd);
  TInt Dist;
  for (int tries = 0; tries < TMath::Mn(NTestNodes, SubGraphNIdV.Len()); tries++) {
    const int NId = NodeIdV[tries];
    BFS.DoBfs(NId, true, ! IsDir, -1, TInt::Mx);
    for (int i = 0; i < SubGraphNIdV.Len(); i++) {
      if (BFS.NIdDistH.IsKeyGetDat(SubGraphNIdV[i], Dist)) {
        DistToCntH.AddDat(Dist) += 1;
      }
    }
  }
  TIntFltKdV DistNbrsPdfV;
  for (int i = 0; i < DistToCntH.Len(); i++) {
    DistNbrsPdfV.Add(TIntFltKd(DistToCntH.GetKey(i), DistToCntH[i]));
  }
  DistNbrsPdfV.Sort();
  EffDiam = TSnap::TSnapDetail::CalcEffDiamPdf(DistNbrsPdfV, 0.9);  // effective diameter (90-th percentile)
  FullDiam = DistNbrsPdfV.Last().Key;                 // approximate full diameter (max shortest path length over the sampled nodes)
  return EffDiam;                                     // average shortest path length
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetBfsFullDiam	(	const PGraph &	Graph,
		const int &	NTestNodes,
		const bool &	IsDir = false
	)

Returns the (approximation of the) Diameter (maximum shortest path length) of a graph (by performing BFS from NTestNodes random starting nodes).

Parameters

IsDir

false: ignore edge directions and consider edges/paths as undirected (in case they are directed).

Definition at line 270 of file bfsdfs.h.

References GetBfsEffDiam().

Referenced by TGStat::TakeDiam().

                                                                                  {
  int FullDiam;
  double EffDiam;
  GetBfsEffDiam(Graph, NTestNodes, IsDir, EffDiam, FullDiam);
  return FullDiam;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

PNGraph TSnap::GetBfsTree	(	const PGraph &	Graph,
		const int &	StartNId,
		const bool &	FollowOut,
		const bool &	FollowIn
	)

Returns a directed Breadth-First-Search tree rooted at StartNId.

Returns a directed graph where a parent points to its child node. Tree is created by following in-links (parameter FollowIn = true) and/or out-links (parameter FollowOut = true).

Definition at line 186 of file bfsdfs.h.

References TNGraph::AddEdge(), TNGraph::AddNode(), TBreathFS< PGraph >::DoBfs(), THash< TKey, TDat, THashFunc >::GetDat(), THash< TKey, TDat, THashFunc >::GetKey(), TNGraph::IsNode(), THash< TKey, TDat, THashFunc >::Len(), TInt::Mx, TNGraph::New(), TBreathFS< PGraph >::NIdDistH, and THash< TKey, TDat, THashFunc >::SortByDat().

                                                                                                          {
  TBreathFS<PGraph> BFS(Graph, false);
  BFS.DoBfs(StartNId, FollowOut, FollowIn, -1, TInt::Mx);
  PNGraph Tree = TNGraph::New();
  BFS.NIdDistH.SortByDat();
  for (int i = 0; i < BFS.NIdDistH.Len(); i++) {
    const int NId = BFS.NIdDistH.GetKey(i);
    const int Dist = BFS.NIdDistH[i];
    typename PGraph::TObj::TNodeI NI = Graph->GetNI(NId);
    if (!Tree->IsNode(NId)) {
      Tree->AddNode(NId);
    }
    if (FollowOut) {
      for (int e = 0; e < NI.GetInDeg(); e++) {
        const int Prev = NI.GetInNId(e);
        if (Tree->IsNode(Prev) && BFS.NIdDistH.GetDat(Prev)==Dist-1) {
          Tree->AddEdge(Prev, NId); }
      }
    }
    if (FollowIn) {
      for (int e = 0; e < NI.GetOutDeg(); e++) {
        const int Prev = NI.GetOutNId(e);
        if (Tree->IsNode(Prev) && BFS.NIdDistH.GetDat(Prev)==Dist-1) {
          Tree->AddEdge(Prev, NId); }
      }
    }
  }
  return Tree;
}

Here is the call graph for this function:

void TSnap::GetBiCon	(	const PUNGraph &	Graph,
		TCnComV &	BiCnComV
	)

Returns all bi-connected components of a Graph.

Parameters

BiCnComV

is a vector of bi-connected components. Each component is defined by the IDs of its member nodes.

Definition at line 42 of file cncom.cpp.

References TCnCom::GetDfsVisitor().

Referenced by GetBiConSzCnt(), GetEdgeBridges(), and GetMxBiCon().

                                                        {
  TBiConVisitor Visitor(Graph->GetNodes());
  TCnCom::GetDfsVisitor(Graph, Visitor);
  BiCnComV = Visitor.CnComV;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSnap::GetBiConSzCnt	(	const PUNGraph &	Graph,
		TIntPrV &	SzCntV
	)

Returns a distribution of bi-connected component sizes.

Parameters

SzCntV

returns a set of pairs (number of nodes in the bi-component, number of such components)

Definition at line 31 of file cncom.cpp.

References THash< TKey, TDat, THashFunc >::AddDat(), GetBiCon(), THash< TKey, TDat, THashFunc >::GetKeyDatPrV(), TVec< TVal, TSizeTy >::Len(), and TVec< TVal, TSizeTy >::Sort().

                                                           {
  TCnComV BiCnComV;
  GetBiCon(Graph, BiCnComV);
  TIntH SzCntH;
  for (int c =0; c < BiCnComV.Len(); c++) {
    SzCntH.AddDat(BiCnComV[c].Len()) += 1;
  }
  SzCntH.GetKeyDatPrV(SzCntV);
  SzCntV.Sort();
}

Here is the call graph for this function:

double TSnap::GetClosenessCentr	(	const PUNGraph &	Graph,
		const int &	NId
	)

Returns Closeness centrality of a given node NId. Closeness centrality of a node is defined as 1/FarnessCentrality.

Definition at line 22 of file centr.cpp.

References GetFarnessCentr().

                                                                {
  const double Farness = GetFarnessCentr(Graph, NId);
  if (Farness != 0.0) { return 1.0/Farness; }
  else { return 0.0; }
}

Here is the call graph for this function:

template<class PGraph >

double TSnap::GetClustCf	(	const PGraph &	Graph,
		int	SampleNodes = -1
	)

Computes the average clustering coefficient as defined in Watts and Strogatz, Collective dynamics of 'small-world' networks.

Considers the graph as undirected.

Definition at line 100 of file triad.h.

References TVec< TVal, TSizeTy >::Empty(), GetTriads(), IAssert, and TVec< TVal, TSizeTy >::Len().

Referenced by TTimeNet::PlotCCfOverTm(), PlotClustCf(), and TGStat::TakeClustCf().

                                                                                {
  TIntTrV NIdCOTriadV;
  GetTriads(Graph, NIdCOTriadV, SampleNodes);
  if (NIdCOTriadV.Empty()) { return 0.0; }
  double SumCcf = 0.0;
  for (int i = 0; i < NIdCOTriadV.Len(); i++) {
    const double OpenCnt = NIdCOTriadV[i].Val2()+NIdCOTriadV[i].Val3();
    if (OpenCnt > 0) {
      SumCcf += NIdCOTriadV[i].Val2() / OpenCnt; }
  }
  IAssert(SumCcf>=0);
  return SumCcf / double(NIdCOTriadV.Len());
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

double TSnap::GetClustCf	(	const PGraph &	Graph,
		TFltPrV &	DegToCCfV,
		int	SampleNodes = -1
	)

Computes the distribution of average clustering coefficient.

Considers the graph as undirected.

Parameters

DegToCCfV	Vector of pairs (degree, avg. clustering coefficient of nodes of that degree).
SampleNodes	If !=-1 then compute clustering coefficient only for a random sample of SampleNodes nodes. Useful for approximate but quick computations.

Definition at line 114 of file triad.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TVec< TVal, TSizeTy >::Gen(), THash< TKey, TDat, THashFunc >::GetKey(), GetTriads(), THash< TKey, TDat, THashFunc >::Len(), TVec< TVal, TSizeTy >::Len(), TVec< TVal, TSizeTy >::Sort(), TInt::Val, TPair< TVal1, TVal2 >::Val1, and TPair< TVal1, TVal2 >::Val2.

                                                                                                    {
  TIntTrV NIdCOTriadV;
  GetTriads(Graph, NIdCOTriadV, SampleNodes);
  THash<TInt, TFltPr> DegSumCnt;
  double SumCcf = 0.0;
  for (int i = 0; i < NIdCOTriadV.Len(); i++) {
    const int D = NIdCOTriadV[i].Val2()+NIdCOTriadV[i].Val3();
    const double Ccf = D!=0 ? NIdCOTriadV[i].Val2() / double(D) : 0.0;
    TFltPr& SumCnt = DegSumCnt.AddDat(Graph->GetNI(NIdCOTriadV[i].Val1).GetDeg());
    SumCnt.Val1 += Ccf;
    SumCnt.Val2 += 1;
    SumCcf += Ccf;
  }
  // get average clustering coefficient for each degree
  DegToCCfV.Gen(DegSumCnt.Len(), 0);
  for (int d = 0; d  < DegSumCnt.Len(); d++) {
    DegToCCfV.Add(TFltPr(DegSumCnt.GetKey(d).Val, double(DegSumCnt[d].Val1()/DegSumCnt[d].Val2())));
  }
  DegToCCfV.Sort();
  return SumCcf / double(NIdCOTriadV.Len());
}

Here is the call graph for this function:

template<class PGraph >

double TSnap::GetClustCf	(	const PGraph &	Graph,
		TFltPrV &	DegToCCfV,
		int64 &	ClosedTriadsX,
		int64 &	OpenTriadsX,
		int	SampleNodes = -1
	)

Computes the distribution of average clustering coefficient as well as the number of open and closed triads in the graph.

Considers the graph as undirected.

Parameters

DegToCCfV	Vector of pairs (degree, avg. clustering coefficient of nodes of that degree).
SampleNodes	If !=-1 then compute clustering coefficient only for a random sample of SampleNodes nodes. Useful for approximate but quick computations.

Definition at line 137 of file triad.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TVec< TVal, TSizeTy >::Gen(), THash< TKey, TDat, THashFunc >::GetKey(), GetTriads(), THash< TKey, TDat, THashFunc >::Len(), TVec< TVal, TSizeTy >::Len(), TVec< TVal, TSizeTy >::Sort(), TInt::Val, TPair< TVal1, TVal2 >::Val1, and TPair< TVal1, TVal2 >::Val2.

                                                                                                                    {
  TIntTrV NIdCOTriadV;
  GetTriads(Graph, NIdCOTriadV, SampleNodes);
  THash<TInt, TFltPr> DegSumCnt;
  double SumCcf = 0.0;
  int64 closedTriads = 0;
  int64 openTriads = 0;
  for (int i = 0; i < NIdCOTriadV.Len(); i++) {
    const int D = NIdCOTriadV[i].Val2()+NIdCOTriadV[i].Val3();
    const double Ccf = D!=0 ? NIdCOTriadV[i].Val2() / double(D) : 0.0;
    closedTriads += NIdCOTriadV[i].Val2;
    openTriads += NIdCOTriadV[i].Val3;
    TFltPr& SumCnt = DegSumCnt.AddDat(Graph->GetNI(NIdCOTriadV[i].Val1).GetDeg());
    SumCnt.Val1 += Ccf;
    SumCnt.Val2 += 1;
    SumCcf += Ccf;
  }
  // get average clustering coefficient for each degree
  DegToCCfV.Gen(DegSumCnt.Len(), 0);
  for (int d = 0; d  < DegSumCnt.Len(); d++) {
    DegToCCfV.Add(TFltPr(DegSumCnt.GetKey(d).Val, DegSumCnt[d].Val1()/DegSumCnt[d].Val2()));
  }
  //if(closedTriads/3 > (uint64) TInt::Mx) { WarnNotify(TStr::Fmt("[%s line %d] %g closed triads.\n", __FILE__, __LINE__, float(closedTriads/3)).CStr());  }
  //if(openTriads > (uint64) TInt::Mx) { WarnNotify(TStr::Fmt("[%s line %d] %g open triads.\n", __FILE__, __LINE__, float(openTriads/3)).CStr());  }
  ClosedTriads = closedTriads/int64(3); // each triad is counted 3 times
  OpenTriads = openTriads;
  DegToCCfV.Sort();
  return SumCcf / double(NIdCOTriadV.Len());
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetCmnNbrs	(	const PGraph &	Graph,
		const int &	NId1,
		const int &	NId2
	)

Returns a number of shared neighbors between a pair of nodes NId1 and NId2.

Definition at line 383 of file triad.h.

Referenced by TTimeNENet::GetTriadEdges().

                                                                      {
  TIntV NbrV;
  return GetCmnNbrs(Graph, NId1, NId2, NbrV);
}

Here is the caller graph for this function:

template<class PGraph >

int TSnap::GetCmnNbrs	(	const PGraph &	Graph,
		const int &	NId1,
		const int &	NId2,
		TIntV &	NbrV
	)

Returns the shared neighbors between a pair of nodes NId1 and NId2.

Definition at line 390 of file triad.h.

References THashSet< TKey, THashFunc >::AddKey(), TVec< TVal, TSizeTy >::Clr(), TVec< TVal, TSizeTy >::Len(), TMath::Mn(), and TVec< TVal, TSizeTy >::Reserve().

                                                                                   {
  if (! Graph->IsNode(NId1) || ! Graph->IsNode(NId2)) { NbrV.Clr(false); return 0; }
  typename PGraph::TObj::TNodeI NI1 = Graph->GetNI(NId1);
  typename PGraph::TObj::TNodeI NI2 = Graph->GetNI(NId2);
  NbrV.Clr(false);
  NbrV.Reserve(TMath::Mn(NI1.GetDeg(), NI2.GetDeg()));
  TIntSet NSet1(NI1.GetDeg()), NSet2(NI2.GetDeg());
  for (int i = 0; i < NI1.GetDeg(); i++) {
    const int nid = NI1.GetNbrNId(i);
    if (nid!=NId1 && nid!=NId2) {
      NSet1.AddKey(nid); }
  }
  for (int i = 0; i < NI2.GetDeg(); i++) {
    const int nid = NI2.GetNbrNId(i);
    if (NSet1.IsKey(nid)) {
      NSet2.AddKey(nid);
    }
  }
  NSet2.GetKeyV(NbrV);
  return NbrV.Len();
}

Here is the call graph for this function:

template<>

int TSnap::GetCmnNbrs< PUNGraph > ( const PUNGraph &  Graph, const int &  NId1, const int &  NId2, TIntV &  NbrV  )

inline

Definition at line 413 of file triad.h.

References TUNGraph::TNodeI::GetDeg(), TUNGraph::TNodeI::GetNbrNId(), IAssert, and TMath::Mn().

                                                                                                      {
  if (! Graph->IsNode(NId1) || ! Graph->IsNode(NId2)) { NbrV.Clr(false); return 0; }
  const TUNGraph::TNodeI NI1 = Graph->GetNI(NId1);
  const TUNGraph::TNodeI NI2 = Graph->GetNI(NId2);
  int i=0, j=0;
  NbrV.Clr(false);
  NbrV.Reserve(TMath::Mn(NI1.GetDeg(), NI2.GetDeg()));
  while (i < NI1.GetDeg() && j < NI2.GetDeg()) {
    const int nid = NI1.GetNbrNId(i);
    while (j < NI2.GetDeg() && NI2.GetNbrNId(j) < nid) { j++; }
    if (j < NI2.GetDeg() && nid==NI2.GetNbrNId(j) && nid!=NId1 && nid!=NId2) {
      IAssert(NbrV.Empty() || NbrV.Last() < nid);
      NbrV.Add(nid);
      j++;
    }
    i++;
  }
  return NbrV.Len();
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetDegCnt	(	const PGraph &	Graph,
		TIntPrV &	DegToCntV
	)

Returns a degree histogram: a set of pairs (degree, number of nodes of such degree)

Definition at line 223 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TVec< TVal, TSizeTy >::Gen(), THash< TKey, TDat, THashFunc >::GetKey(), THash< TKey, TDat, THashFunc >::Len(), and TVec< TVal, TSizeTy >::Sort().

                                                        {
  TIntH DegToCntH;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    DegToCntH.AddDat(NI.GetDeg())++; }
  DegToCntV.Gen(DegToCntH.Len(), 0);
  for (int i = 0; i < DegToCntH.Len(); i++) {
    DegToCntV.Add(TIntPr(DegToCntH.GetKey(i), DegToCntH[i])); }
  DegToCntV.Sort();
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetDegCnt	(	const PGraph &	Graph,
		TFltPrV &	DegToCntV
	)

Returns a degree histogram: a set of pairs (degree, number of nodes of such degree)

Definition at line 234 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TVec< TVal, TSizeTy >::Gen(), THash< TKey, TDat, THashFunc >::GetKey(), THash< TKey, TDat, THashFunc >::Len(), and TVec< TVal, TSizeTy >::Sort().

                                                        {
  TIntH DegToCntH;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    DegToCntH.AddDat(NI.GetDeg())++; }
  DegToCntV.Gen(DegToCntH.Len(), 0);
  for (int i = 0; i < DegToCntH.Len(); i++) {
    DegToCntV.Add(TFltPr(DegToCntH.GetKey(i).Val, DegToCntH[i].Val)); }
  DegToCntV.Sort();
}

Here is the call graph for this function:

double TSnap::GetDegreeCentr	(	const PUNGraph &	Graph,
		const int &	NId
	)

Returns Degree centrality of a given node NId. Degree centrality if a node is defined as its degree/(N-1), where N is the number of nodes in the network.

Definition at line 5 of file centr.cpp.

                                                             {
  if (Graph->GetNodes() > 1) {
    return double(Graph->GetNI(NId).GetDeg())/double(Graph->GetNodes()-1); }
  else { return 0.0; }
}

template<class PGraph >

void TSnap::GetDegSeqV	(	const PGraph &	Graph,
		TIntV &	DegV
	)

Returns a degree sequence vector.

Definition at line 245 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), and TVec< TVal, TSizeTy >::Gen().

Referenced by GenConfModel().

                                                  {
  DegV.Gen(Graph->GetNodes(), 0);
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    DegV.Add(NI.GetDeg());
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::GetDegSeqV	(	const PGraph &	Graph,
		TIntV &	InDegV,
		TIntV &	OutDegV
	)

Returns an in- and out-degree sequence vectors.

Definition at line 253 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), and TVec< TVal, TSizeTy >::Gen().

                                                                    {
  InDegV.Gen(Graph->GetNodes(), 0);
  OutDegV.Gen(Graph->GetNodes(), 0);
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    InDegV.Add(NI.GetInDeg());
    OutDegV.Add(NI.GetOutDeg());
  }
}

Here is the call graph for this function:

template<class PGraph , class TEdgeDat >

PGraph TSnap::GetEDatSubGraph	(	const PGraph &	Graph,
		const TEdgeDat &	EDat,
		const int &	Cmp
	)

Returns a subgraph of graph Graph with edges where edge data matches the parameters.

EDat provides the value for edge data matching. Cmp determines the comparison function. Edges whose edge data matches EDat are included in the resulting subgraph as well as all the nodes which connect to at least one edge in the subgraph. Node IDs are preserved. Nodes in the resulting subgraph have the same node IDs as nodes in Graph.

Values of Cmp can be -1, 0, or +1. If Cmp is -1, edges with edge data less than EDat are included in the resulting subgraph. If Cmp equals 0, the values of edge data and EDat have to match. If Cmp is +1, edge data has to be greater than EDat.

Definition at line 248 of file subgraph.h.

References CAssert, gfEdgeDat, and HasGraphFlag.

                                                                                  {
  CAssert(HasGraphFlag(typename PGraph::TObj, gfEdgeDat));
  PGraph NewGraphPt = PGraph::TObj::New();
  typename PGraph::TObj& NewGraph = *NewGraphPt;
  for (typename PGraph::TObj::TEdgeI EI = Graph->BegEI(); EI < Graph->EndEI(); EI++) {
    if ((Cmp==1 && EI()>EDat) || (Cmp==-1 && EI()<EDat) || (Cmp==0 && EI()==EDat)) {
      if (! NewGraph.IsNode(EI.GetSrcNId())) {
        NewGraph.AddNode(Graph->GetNI(EI.GetSrcNId()));
      }
      if (! NewGraph.IsNode(EI.GetDstNId())) {
        NewGraph.AddNode(Graph->GetNI(EI.GetDstNId()));
      }
      NewGraph.AddEdge(EI); 
    }
  }
  return NewGraphPt;
}

template<class PGraph , class TEdgeDat >

PGraph TSnap::GetEDatSubGraph	(	const PGraph &	Graph,
		const TIntV &	NIdV,
		const TEdgeDat &	EDat,
		const int &	Cmp
	)

Returns a subgraph of graph Graph with NIdV nodes and edges where edge data matches the parameters.

The resulting subgraph contains all the nodes from Graph, which have node IDs in the NIdV vector and edges with both nodes in NIdV and whose edge data matches the parameters. Node IDs are preserved. Nodes in the resulting subgraph have the same node IDs as nodes in Graph.

EDat provides the value for edge data matching. Cmp determines the comparison function. Values of Cmp can be -1, 0, or +1. If Cmp is -1, edges with edge data less than EDat are included in the resulting subgraph. If Cmp equals 0, the values of edge data and EDat have to match. If Cmp is +1, edge data has to be greater than EDat.

Definition at line 268 of file subgraph.h.

References CAssert, gfEdgeDat, HasGraphFlag, and TVec< TVal, TSizeTy >::Len().

                                                                                                     {
  CAssert(HasGraphFlag(typename PGraph::TObj, gfEdgeDat));
  PGraph NewGraphPt = PGraph::TObj::New();
  typename PGraph::TObj& NewGraph = *NewGraphPt;
  NewGraph.Reserve(NIdV.Len(), -1);
  for (int n = 0; n < NIdV.Len(); n++) {
    NewGraph.AddNode(Graph->GetNI(NIdV[n])); 
  }
  for (typename PGraph::TObj::TEdgeI EI = Graph->BegEI(); EI < Graph->EndEI(); EI++) {
    if (NewGraph.IsNode(EI.GetSrcNId()) && NewGraph.IsNode(EI.GetDstNId()) &&
     ((Cmp==1 && EI()>EDat)|| (Cmp==-1 && EI()<EDat) || (Cmp==0 && EI()==EDat))) {
      NewGraph.AddEdge(EI); }
  }
  NewGraph.Defrag();
  return NewGraphPt;
}

Here is the call graph for this function:

void TSnap::GetEdgeBridges	(	const PUNGraph &	Graph,
		TIntPrV &	EdgeV
	)

Returns bridge edges of a Graph.

Edge is a bridge if, when removed, increases the number of connected components. See http://en.wikipedia.org/wiki/Bridge_(graph_theory)

Definition at line 55 of file cncom.cpp.

References THashSet< TKey, THashFunc >::AddKey(), GetBiCon(), THashSet< TKey, THashFunc >::GetKeyV(), TVec< TVal, TSizeTy >::Len(), TMath::Mn(), and TMath::Mx().

Referenced by Get1CnCom(), and Get1CnComSzCnt().

                                                           {
  TCnComV BiCnComV;
  GetBiCon(Graph, BiCnComV);
  TIntPrSet EdgeSet;
  for (int c = 0; c < BiCnComV.Len(); c++) {
    const TIntV& NIdV = BiCnComV[c].NIdV; 
    if (NIdV.Len() == 2) {
      EdgeSet.AddKey(TIntPr(TMath::Mn(NIdV[0], NIdV[1]), TMath::Mx(NIdV[0], NIdV[1]))); 
    }
  }
  EdgeSet.GetKeyV(EdgeV);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<typename PGraph >

void TSnap::GetEdgesInOut	(	const PGraph &	Graph,
		const TIntV &	NIdV,
		int &	EdgesInX,
		int &	EdgesOutX
	)

Returns the number of edges between the nodes NIdV and the edges pointing outside the set NIdV.

Parameters

EdgesIn	Number of edges between the nodes NIdV.
EdgesOut	Number of edges between the nodes in NIdV and the rest of the graph.

Definition at line 66 of file cmty.h.

References THashSet< TKey, THashFunc >::AddKey(), and TVec< TVal, TSizeTy >::Len().

Referenced by TLocClustStat::TCutInfo::TCutInfo().

                                                                                        {
  EdgesIn=0;
  EdgesOut=0;
  TIntSet NIdSet(NIdV.Len());
  for (int e = 0; e < NIdV.Len(); e++) {
    NIdSet.AddKey(NIdV[e]); }
  for (int e = 0; e < NIdV.Len(); e++) {
    typename PGraph::TObj::TNodeI NI = Graph->GetNI(NIdV[e]);
    for (int i = 0; i < NI.GetOutDeg(); i++) {
      if (NIdSet.IsKey(NI.GetOutNId(i))) { EdgesIn += 1; }
      else { EdgesOut += 1; }
    }
  }
  EdgesIn /= 2;
}

Here is the call graph for this function:

Here is the caller graph for this function:

PUNGraph TSnap::GetEgonet	(	const PUNGraph &	Graph,
		const int	CtrNId,
		int &	ArndEdges
	)

Returns the egonet of node CtrNId as center in undirected graph Graph. And returns number of edges around the egonet.

Definition at line 82 of file subgraph.cpp.

References TUNGraph::AddEdge(), TUNGraph::AddNode(), TUNGraph::TNodeI::GetInDeg(), TUNGraph::TNodeI::GetInNId(), TUNGraph::IsEdge(), TUNGraph::IsNode(), and TUNGraph::New().

Referenced by AddEgonetFeatures().

                                                                            {
  PUNGraph NewGraphPt = TUNGraph::New();
  TUNGraph& NewGraph = *NewGraphPt;
  NewGraph.AddNode(CtrNId);
  const TUNGraph::TNodeI& CtrNode = Graph->GetNI(CtrNId);
  for (int i = 0; i < CtrNode.GetInDeg(); ++i) {
    NewGraph.AddNode(CtrNode.GetInNId(i));
  }
  ArndEdges = 0;
  for (int i = 0; i < CtrNode.GetInDeg(); ++i) {
    int NbrNId = CtrNode.GetInNId(i);
    const TUNGraph::TNodeI& NbrNode = Graph->GetNI(NbrNId);
    for (int j = 0; j < NbrNode.GetInDeg(); ++j) {
      int NbrNbrNId = NbrNode.GetInNId(j);
      if (NewGraph.IsNode(NbrNbrNId)) {
        if (!NewGraph.IsEdge(NbrNId, NbrNbrNId)) {
          NewGraph.AddEdge(NbrNId, NbrNbrNId);
        }
      } else {
        ArndEdges++;
      }
    }
  }
  return NewGraphPt;
}

Here is the call graph for this function:

Here is the caller graph for this function:

PNGraph TSnap::GetEgonet	(	const PNGraph &	Graph,
		const int	CtrNId,
		int &	InEdges,
		int &	OutEdges
	)

Returns the egonet of node CtrNId as center in directed graph Graph. And returns number of edges go in and out the egonet.

Definition at line 108 of file subgraph.cpp.

References TNGraph::AddEdge(), TNGraph::AddNode(), TNGraph::TNodeI::GetDeg(), TNGraph::TNodeI::GetInDeg(), TNGraph::TNodeI::GetInNId(), TNGraph::TNodeI::GetNbrNId(), TNGraph::GetNI(), TNGraph::TNodeI::GetOutDeg(), TNGraph::TNodeI::GetOutNId(), TNGraph::IsNode(), and TNGraph::New().

                                                                                       {
  PNGraph NewGraphPt = TNGraph::New();
  TNGraph& NewGraph = *NewGraphPt;
  NewGraph.AddNode(CtrNId);
  const TNGraph::TNodeI& CtrNode = Graph->GetNI(CtrNId);
  for (int i = 0; i < CtrNode.GetDeg(); ++i) {
    NewGraph.AddNode(CtrNode.GetNbrNId(i));
  }
  InEdges = 0;
  OutEdges = 0;
  for (int i = 0; i < CtrNode.GetDeg(); ++i) {
    int NbrNId = CtrNode.GetNbrNId(i);
    const TNGraph::TNodeI& NbrNode = Graph->GetNI(NbrNId);
    for (int j = 0; j < NbrNode.GetInDeg(); ++j) {
      int NbrNbrNId = NbrNode.GetInNId(j);
      if (NewGraph.IsNode(NbrNbrNId)) {
        NewGraph.AddEdge(NbrNbrNId, NbrNId);
      } else {
        InEdges++;
      }
    }
    for (int j = 0; j < NbrNode.GetOutDeg(); ++j) {
      int NbrNbrNId = NbrNode.GetOutNId(j);
      if (!NewGraph.IsNode(NbrNbrNId)) {
        OutEdges++;
      }
    }
  }
  return NewGraphPt;
}

Here is the call graph for this function:

void TSnap::GetEigenVectorCentr	(	const PUNGraph &	Graph,
		TIntFltH &	NIdEigenH,
		const double &	Eps = 1e-4,
		const int &	MaxIter = 100
	)

Computes Eigenvector Centrality of all nodes in the network Eigenvector Centrality of a node N is defined recursively as the average of centrality values of N's neighbors in the network.

Definition at line 135 of file centr.cpp.

References THash< TKey, TDat, THashFunc >::AddDat(), THash< TKey, TDat, THashFunc >::Gen(), THash< TKey, TDat, THashFunc >::GetDat(), THash< TKey, TDat, THashFunc >::GetKey(), IAssert, THash< TKey, TDat, THashFunc >::Len(), and TVec< TVal, TSizeTy >::Len().

                                                                                                            {
  const int NNodes = Graph->GetNodes();
  NIdEigenH.Gen(NNodes);
  // initialize vector values
  for (TUNGraph::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    NIdEigenH.AddDat(NI.GetId(), 1.0/NNodes);
    IAssert(NI.GetId() == NIdEigenH.GetKey(NIdEigenH.Len()-1));
  }
  TFltV TmpV(NNodes);
  for (int iter = 0; iter < MaxIter; iter++) {
    int j = 0;
    // add neighbor values
    for (TUNGraph::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++, j++) {
      TmpV[j] = 0;
      for (int e = 0; e < NI.GetOutDeg(); e++) {
        TmpV[j] += NIdEigenH.GetDat(NI.GetOutNId(e)); }
    }

    // normalize
    double sum = 0;
    for (int i = 0; i < TmpV.Len(); i++) {
      sum += (TmpV[i]*TmpV[i]);
    }
    sum = sqrt(sum);
    for (int i = 0; i < TmpV.Len(); i++) {
      TmpV[i] /= sum;
    }

    // compute difference
    double diff = 0.0;
    j = 0;
    for (TUNGraph::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++, j++) {
      diff += fabs(NIdEigenH.GetDat(NI.GetId())-TmpV[j]);
    }

    // set new values
    j = 0;
    for (TUNGraph::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++, j++) {
      NIdEigenH.AddDat(NI.GetId(), TmpV[j]);
    }

    if (diff < Eps) {
      break;
    }
  }
}

Here is the call graph for this function:

void TSnap::GetEigVals	(	const PUNGraph &	Graph,
		const int &	EigVals,
		TFltV &	EigValV
	)

Computes top EigVals eigenvalues of the adjacency matrix representing a given undirected Graph.

Definition at line 308 of file gsvd.cpp.

References TSparseSVD::Lanczos(), TVec< TVal, TSizeTy >::Len(), TSparseSVD::SimpleLanczos(), TVec< TVal, TSizeTy >::Sort(), and ssotFull.

Referenced by PlotEigValDistr(), and PlotEigValRank().

                                                                           {
  // Lanczos
  TUNGraphMtx GraphMtx(Graph);
  //const int Nodes = Graph->GetNodes();
  //int CalcVals = int(2*EigVals);
  //if (CalcVals > Nodes) { CalcVals = Nodes; }
  //while (EigValV.Len() < EigVals && CalcVals < 3*EigVals) {
  try {
    if (EigVals > 4) { 
      TSparseSVD::SimpleLanczos(GraphMtx, 2*EigVals, EigValV, false); }
    else { TFltVV EigVecVV; // this is much more precise, but also much slower
      TSparseSVD::Lanczos(GraphMtx, EigVals, 3*EigVals, ssotFull, EigValV, EigVecVV, false); }
  }
  catch(...) {
    printf("\n  ***EXCEPTION:  TRIED %d GOT %d values** \n", 2*EigVals, EigValV.Len()); }
  if (EigValV.Len() < EigVals) {
    printf("  ***TRIED %d GOT %d values** \n", 2*EigVals, EigValV.Len()); }
  //  CalcVals += EigVals;
  //}
  EigValV.Sort(false);
  /*if (EigValV.Len() > EigVals) {
    EigValV.Del(EigVals, EigValV.Len()-1); }
  else {
    while (EigValV.Len() < EigVals) EigValV.Add(1e-6); 
  }
  IAssert(EigValV.Len() == EigVals);*/
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSnap::GetEigVec	(	const PUNGraph &	Graph,
		TFltV &	EigVecV
	)

Computes the leading eigenvector of the adjacency matrix representing a given undirected Graph.

Definition at line 336 of file gsvd.cpp.

References TVVec< TVal >::GetCol(), IsAllValVNeg(), TSparseSVD::Lanczos(), and ssotFull.

                                                      {
  TUNGraphMtx GraphMtx(Graph);
  TFltV EigValV;
  TFltVV EigVecVV;
  TSparseSVD::Lanczos(GraphMtx, 1, 8, ssotFull, EigValV, EigVecVV, false);
  EigVecVV.GetCol(0, EigVecV); // vector components are not sorted!!!
  IsAllValVNeg(EigVecV, true);
}

Here is the call graph for this function:

void TSnap::GetEigVec	(	const PUNGraph &	Graph,
		const int &	EigVecs,
		TFltV &	EigValV,
		TVec< TFltV > &	EigVecV
	)

Computes top EigVecs eigenvalues and eigenvectors of the adjacency matrix representing a given undirected Graph.

Definition at line 346 of file gsvd.cpp.

References TVec< TVal, TSizeTy >::Add(), TVVec< TVal >::GetCol(), IsAllValVNeg(), TSparseSVD::Lanczos(), TVec< TVal, TSizeTy >::Last(), TVec< TVal, TSizeTy >::Len(), TVec< TVal, TSizeTy >::Sort(), and ssotFull.

                                                                                                {
  const int Nodes = Graph->GetNodes();
  // Lanczos
  TUNGraphMtx GraphMtx(Graph);
  int CalcVals = int(2*EigVecs);
  if (CalcVals > Nodes) { CalcVals = Nodes; }
  TFltVV EigVecVV;
  //while (EigValV.Len() < EigVecs && CalcVals < 10*EigVecs) {
  try {
    TSparseSVD::Lanczos(GraphMtx, EigVecs, 2*EigVecs, ssotFull, EigValV, EigVecVV, false); }
  catch(...) {
    printf("\n  ***EXCEPTION:  TRIED %d GOT %d values** \n", CalcVals, EigValV.Len()); }
  if (EigValV.Len() < EigVecs) {
    printf("  ***TRIED %d GOT %d values** \n", CalcVals, EigValV.Len()); }
  //  CalcVals += EigVecs;
  //}
  TFltIntPrV EigValIdV;
  for (int i = 0; i < EigValV.Len(); i++) {
    EigValIdV.Add(TFltIntPr(EigValV[i], i)); 
  }
  EigValIdV.Sort(false);
  EigValV.Sort(false);
  for (int v = 0; v < EigValIdV.Len(); v++) { // vector components are not sorted!!!
    EigVecV.Add();
    EigVecVV.GetCol(EigValIdV[v].Val2, EigVecV.Last());
  }
  IsAllValVNeg(EigVecV[0], true);
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::GetESubGraph	(	const PGraph &	Graph,
		const TIntV &	EIdV
	)

Returns a subgraph of graph Graph with EIdV edges.

The resulting subgraph contains all the edges from Graph, which have edge IDs in the EIdV vector and all the nodes which connect to at least one edge in EIdV. Node and edge IDs are preserved. Nodes and edges in the resulting subgraph have the same IDs as in Graph.

Use this function for multi-graphs, where the edges have edge IDs.

Definition at line 206 of file subgraph.h.

References CAssert, gfMultiGraph, HasGraphFlag, IAssert, and TVec< TVal, TSizeTy >::Len().

Referenced by GetRndESubGraph(), and TTimeNENet::TimeGrowth().

                                                            {
  CAssert(HasGraphFlag(typename PGraph::TObj, gfMultiGraph));
  PGraph NewGraphPt = PGraph::TObj::New();
  typename PGraph::TObj& NewGraph = *NewGraphPt;
  NewGraph.Reserve(-1, EIdV.Len());
  for (int edge = 0; edge < EIdV.Len(); edge++) {
    const int EId = EIdV[edge];
    IAssert(Graph->IsEdge(EId));
    const typename PGraph::TObj::TEdgeI EI = Graph->GetEI(EId);
    if (! NewGraph.IsNode(EI.GetSrcNId())) {
      NewGraph.AddNode(Graph->GetNI(EI.GetSrcNId())); 
    }
    if (! NewGraph.IsNode(EI.GetDstNId())) {
      NewGraph.AddNode(Graph->GetNI(EI.GetDstNId())); 
    }
    NewGraph.AddEdge(EI);
  }
  return NewGraphPt;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

PGraph TSnap::GetESubGraph	(	const PGraph &	Graph,
		const TIntPrV &	EdgeV
	)

Definition at line 227 of file subgraph.h.

References TVec< TVal, TSizeTy >::Len().

                                                               {
  PGraph NewGraphPt = PGraph::TObj::New();
  typename PGraph::TObj& NewGraph = *NewGraphPt;
  NewGraph.Reserve(-1, EdgeV.Len());
  for (int edge = 0; edge < EdgeV.Len(); edge++) {
    const int SrcNId = EdgeV[edge].Val1;
    const int DstNId = EdgeV[edge].Val2;
    const typename PGraph::TObj::TEdgeI EI = Graph->GetEI(SrcNId, DstNId);
    if (! NewGraph.IsNode(EI.GetSrcNId())) {
      NewGraph.AddNode(Graph->GetNI(EI.GetSrcNId())); 
    }
    if (! NewGraph.IsNode(EI.GetDstNId())) {
      NewGraph.AddNode(Graph->GetNI(EI.GetDstNId())); 
    }
    NewGraph.AddEdge(EI);
  }
  return NewGraphPt;
}

Here is the call graph for this function:

double TSnap::GetFarnessCentr	(	const PUNGraph &	Graph,
		const int &	NId
	)

Returns Farness centrality of a given node NId. Farness centrality of a node is the average shortest path length to all other nodes that reside is the same connected component as the given node.

Definition at line 11 of file centr.cpp.

References THashKeyDatI< TKey, TDat >::EndI, and TInt::Mx.

Referenced by GetClosenessCentr().

                                                              {
  TIntH NDistH(Graph->GetNodes());
  TSnap::GetShortPath<PUNGraph>(Graph, NId, NDistH, true, TInt::Mx);
  double sum = 0;
  for (TIntH::TIter I = NDistH.BegI(); I < NDistH.EndI(); I++) {
    sum += I->Dat();
  }
  if (NDistH.Len() > 1) { return sum/double(NDistH.Len()-1); }
  else { return 0.0; }
}

Here is the caller graph for this function:

TStr TSnap::GetFlagStr

(

const TGraphFlag &

GraphFlag

)

Returns a string representation of a flag.

Definition at line 5 of file gbase.cpp.

References FailR, gfBipart, gfDirected, gfEdgeDat, gfMultiGraph, gfNodeDat, gfSources, and gfUndef.

Referenced by TBigNet< TNodeData, IsDir >::DumpFlags(), and PrintInfo().

                                             {
  switch (GraphFlag) {
    case gfUndef : return "Undef";
    case gfDirected : return "Directed";
    case gfMultiGraph : return "Multigraph";
    case gfNodeDat : return "NodeDat";
    case gfEdgeDat : return "EdgeDat";
    case gfSources : return "Sources";
    case gfBipart : return "Bipartite";
    default: FailR("Unknown graph type");
  };
  return TStr();
}

Here is the caller graph for this function:

template<class PGraph >

void TSnap::GetHits	(	const PGraph &	Graph,
		TIntFltH &	NIdHubH,
		TIntFltH &	NIdAuthH,
		const int &	MaxIter = 20
	)

HITS: Hubs and Authorities For more info see: http://en.wikipedia.org/wiki/HITS_algorithm)

Definition at line 111 of file centr.h.

References THash< TKey, TDat, THashFunc >::AddDat(), THash< TKey, TDat, THashFunc >::Gen(), THash< TKey, TDat, THashFunc >::GetDat(), THash< TKey, TDat, THashFunc >::Len(), and TMath::Sqr().

                                                                                             {
  const int NNodes = Graph->GetNodes();
  NIdHubH.Gen(NNodes);
  NIdAuthH.Gen(NNodes);
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    NIdHubH.AddDat(NI.GetId(), 1.0);
    NIdAuthH.AddDat(NI.GetId(), 1.0);
  }
  double Norm=0;
  for (int iter = 0; iter < MaxIter; iter++) {
    // update authority scores
    Norm = 0;
    for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
      double& Auth = NIdAuthH.GetDat(NI.GetId()).Val;
      Auth = 0;
      for (int e = 0; e < NI.GetInDeg(); e++) {
        Auth +=  NIdHubH.GetDat(NI.GetInNId(e)); }
      Norm += Auth*Auth;
    }
    Norm = sqrt(Norm);
    for (int i = 0; i < NIdAuthH.Len(); i++) { NIdAuthH[i] /= Norm; }
    // update hub scores
    for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
      double& Hub = NIdHubH.GetDat(NI.GetId()).Val;
      Hub = 0;
      for (int e = 0; e < NI.GetOutDeg(); e++) {
        Hub += NIdAuthH.GetDat(NI.GetOutNId(e)); }
      Norm += Hub*Hub;
    }
    Norm = sqrt(Norm);
    for (int i = 0; i < NIdHubH.Len(); i++) { NIdHubH[i] /= Norm; }
  }
  // make sure Hub and Authority scores normalize to L2 norm 1
  Norm = 0.0;
  for (int i = 0; i < NIdHubH.Len(); i++) { Norm += TMath::Sqr(NIdHubH[i]); }
  Norm = sqrt(Norm);
  for (int i = 0; i < NIdHubH.Len(); i++) { NIdHubH[i] /= Norm; }
  Norm = 0.0;
  for (int i = 0; i < NIdAuthH.Len(); i++) { Norm += TMath::Sqr(NIdAuthH[i]); }
  Norm = sqrt(Norm);
  for (int i = 0; i < NIdAuthH.Len(); i++) { NIdAuthH[i] /= Norm; }
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetInDegCnt	(	const PGraph &	Graph,
		TIntPrV &	DegToCntV
	)

Returns an in-degree histogram: a set of pairs (in-degree, number of nodes of such in-degree)

Definition at line 179 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TVec< TVal, TSizeTy >::Gen(), THash< TKey, TDat, THashFunc >::GetKey(), THash< TKey, TDat, THashFunc >::Len(), and TVec< TVal, TSizeTy >::Sort().

Referenced by PlotInDegDistr(), and TGStat::TakeDegDistr().

                                                          {
  TIntH DegToCntH;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    DegToCntH.AddDat(NI.GetInDeg())++; }
  DegToCntV.Gen(DegToCntH.Len(), 0);
  for (int i = 0; i < DegToCntH.Len(); i++) {
    DegToCntV.Add(TIntPr(DegToCntH.GetKey(i), DegToCntH[i])); }
  DegToCntV.Sort();
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::GetInDegCnt	(	const PGraph &	Graph,
		TFltPrV &	DegToCntV
	)

Returns an in-degree histogram: a set of pairs (in-degree, number of nodes of such in-degree)

Definition at line 190 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TVec< TVal, TSizeTy >::Gen(), THash< TKey, TDat, THashFunc >::GetKey(), THash< TKey, TDat, THashFunc >::Len(), and TVec< TVal, TSizeTy >::Sort().

                                                          {
  TIntH DegToCntH;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    DegToCntH.AddDat(NI.GetInDeg())++; }
  DegToCntV.Gen(DegToCntH.Len(), 0);
  for (int i = 0; i < DegToCntH.Len(); i++) {
    DegToCntV.Add(TFltPr(DegToCntH.GetKey(i).Val, DegToCntH[i].Val)); }
  DegToCntV.Sort();
}

Here is the call graph for this function:

void TSnap::GetInvParticipRat	(	const PUNGraph &	Graph,
		int	MaxEigVecs,
		int	TimeLimit,
		TFltPrV &	EigValIprV
	)

Computes Inverse participation ratio of a given graph. See Spectra of "real-world" graphs: Beyond the semicircle law by Farkas, Derenyi, Barabasi and Vicsek

Definition at line 377 of file gsvd.cpp.

References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Clr(), TVec< TVal, TSizeTy >::Empty(), TVVec< TVal >::GetCol(), TVVec< TVal >::GetCols(), TSnap::TSnapDetail::GetInvParticipRatEig(), TExeTm::GetStr(), TSparseSVD::Lanczos2(), TVec< TVal, TSizeTy >::Len(), TMath::Mn(), TVec< TVal, TSizeTy >::Sort(), and ssotFull.

Referenced by PlotInvParticipRat().

                                                                                                  {
  TUNGraphMtx GraphMtx(Graph);
  TFltVV EigVecVV;
  TFltV EigValV;
  TExeTm ExeTm;
  if (MaxEigVecs<=1) { MaxEigVecs=1000; }
  int EigVecs = TMath::Mn(Graph->GetNodes(), MaxEigVecs);
  printf("start %d vecs...", EigVecs);
  try {
    TSparseSVD::Lanczos2(GraphMtx, EigVecs, TimeLimit, ssotFull, EigValV, EigVecVV, false);
  } catch(...) {
    printf("\n  ***EXCEPTION:  TRIED %d GOT %d values** \n", EigVecs, EigValV.Len()); }
  printf("  ***TRIED %d GOT %d values in %s\n", EigVecs, EigValV.Len(), ExeTm.GetStr());
  TFltV EigVec;
  EigValIprV.Clr();
  if (EigValV.Empty()) { return; }
  for (int v = 0; v < EigVecVV.GetCols(); v++) {
    EigVecVV.GetCol(v, EigVec);
    EigValIprV.Add(TFltPr(EigValV[v], TSnapDetail::GetInvParticipRatEig(EigVec)));
  }
  EigValIprV.Sort();
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

PGraph TSnap::GetKCore	(	const PGraph &	Graph,
		const int &	K
	)

Returns the K-core of a graph. If the core of order K does not exist the function returns an empty graph.

Definition at line 106 of file kcore.h.

References TKCore< PGraph >::GetCoreK(), TKCore< PGraph >::GetNIdV(), and GetSubGraph().

                                                   {
  TKCore<PGraph> KCore(Graph);
  KCore.GetCoreK(K);
  return TSnap::GetSubGraph(Graph, KCore.GetNIdV());
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetKCoreEdges	(	const PGraph &	Graph,
		TIntPrV &	CoreIdSzV
	)

Returns the number of edges in each core of order K (where K=0, 1, ...)

Definition at line 126 of file kcore.h.

References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Clr(), TKCore< PGraph >::GetCoreEdges(), TKCore< PGraph >::GetCurK(), and TKCore< PGraph >::GetNextCore().

Referenced by PlotKCoreEdges().

                                                           {
  TKCore<PGraph> KCore(Graph);
  CoreIdSzV.Clr();
  CoreIdSzV.Add(TIntPr(0, Graph->GetEdges()));
  for (int i = 1; KCore.GetNextCore() > 0; i++) {
    CoreIdSzV.Add(TIntPr(i, KCore.GetCoreEdges()));
  }
  return KCore.GetCurK();
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

int TSnap::GetKCoreNodes	(	const PGraph &	Graph,
		TIntPrV &	CoreIdSzV
	)

Returns the number of nodes in each core of order K (where K=0, 1, ...)

Definition at line 114 of file kcore.h.

References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Clr(), TKCore< PGraph >::GetCoreNodes(), TKCore< PGraph >::GetCurK(), and TKCore< PGraph >::GetNextCore().

Referenced by PlotKCoreNodes().

                                                           {
  TKCore<PGraph> KCore(Graph);
  CoreIdSzV.Clr();
  CoreIdSzV.Add(TIntPr(0, Graph->GetNodes()));
  for (int i = 1; KCore.GetNextCore() > 0; i++) {
    CoreIdSzV.Add(TIntPr(i, KCore.GetCoreNodes()));
  }
  return KCore.GetCurK();
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

int TSnap::GetLen2Paths	(	const PGraph &	Graph,
		const int &	NId1,
		const int &	NId2
	)

Returns the number of length 2 directed paths between a pair of nodes NId1, NId2 (NId1 –> U –> NId2).

Definition at line 436 of file triad.h.

                                                                        {
  TIntV NbrV;
  return GetLen2Paths(Graph, NId1, NId2, NbrV);
}

template<class PGraph >

int TSnap::GetLen2Paths	(	const PGraph &	Graph,
		const int &	NId1,
		const int &	NId2,
		TIntV &	NbrV
	)

Returns the 2 directed paths between a pair of nodes NId1, NId2 (NId1 –> U –> NId2).

NbrV intermediary stores nodes U.

Definition at line 444 of file triad.h.

References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Clr(), TVec< TVal, TSizeTy >::Len(), and TVec< TVal, TSizeTy >::Reserve().

                                                                                     {
  const typename PGraph::TObj::TNodeI NI = Graph->GetNI(NId1);
  NbrV.Clr(false);
  NbrV.Reserve(NI.GetOutDeg());
  for (int e = 0; e < NI.GetOutDeg(); e++) {
    const typename PGraph::TObj::TNodeI MidNI = Graph->GetNI(NI.GetOutNId(e));
    if (MidNI.IsOutNId(NId2)) {
      NbrV.Add(MidNI.GetId());
    }
  }
  return NbrV.Len();
}

Here is the call graph for this function:

int TSnap::GetMaxFlowIntEK	(	PNEANet &	Net,
		const int &	SrcNId,
		const int &	SnkNId
	)

Returns the maximum integer valued flow in the network Net from source SrcNId to sink SnkNId.

Implements max flow using the Edmonds-Karp algorithm. http://en.wikipedia.org/wiki/Edmonds%E2%80%93Karp_algorithm Although the asymptotic run time of Edmonds-Karp is worse than that of Push Relabel, in practice Edmonds Karp works very well, especially if the network is sparse. Unless the degree of each node is on the order of the number of nodes, it is best to use Edmonds Karp over Push Relabel.

Definition at line 105 of file flow.cpp.

References CapAttrName(), FindAugV(), TNEANet::TEdgeI::GetDstNId(), TNEANet::TEdgeI::GetSrcNId(), IAssert, and TVec< TVal, TSizeTy >::Len().

                                                                         {
  IAssert(Net->IsNode(SrcNId));
  IAssert(Net->IsNode(SnkNId));
  if (SrcNId == SnkNId) { return 0; }
  int CapIndex = Net->GetIntAttrIndE(CapAttrName);
  TIntV Flow(Net->GetMxEId());
  // Initialize flow values to 0, and make sure capacities are nonnegative
  for (TNEANet::TEdgeI EI = Net->BegEI(); EI != Net->EndEI(); EI++) {
    IAssert(Net->GetIntAttrIndDatE(EI, CapIndex) >= 0);
    Flow[EI.GetId()] = 0;
  }
  // Return 0 if user attempts to flow from a node to itself.
  if (SrcNId == SnkNId) { return 0; }
  int MaxFlow = 0, MinAug, CurNId;
  while (true) {
    TIntV MidToSrcAugV; TIntV MidToSnkAugV;
    TIntQ FwdNodeQ; TIntQ BwdNodeQ;
    TIntH PredEdgeH; TIntH SuccEdgeH;
    MinAug = FindAugV(Net, CapIndex, Flow, FwdNodeQ, PredEdgeH, BwdNodeQ, SuccEdgeH, MidToSrcAugV, MidToSnkAugV, SrcNId, SnkNId);
    if (MinAug == 0) { break; }
    MaxFlow += MinAug;
    CurNId = SrcNId;
    for (int i = MidToSrcAugV.Len() - 1; i >= 0; i--) {
      int NextEId = MidToSrcAugV[i];
      const TNEANet::TEdgeI &EI = Net->GetEI(NextEId);
      if (EI.GetSrcNId() == CurNId) {
        Flow[NextEId] += MinAug;
        CurNId = EI.GetDstNId();
      } else {
        Flow[NextEId] -= MinAug;
        CurNId = EI.GetSrcNId();
      }
    }
    for (int i = 0; i < MidToSnkAugV.Len(); i++) {
      int NextEId = MidToSnkAugV[i];
      const TNEANet::TEdgeI &EI = Net->GetEI(NextEId);
      if (EI.GetSrcNId() == CurNId) {
        Flow[NextEId] += MinAug;
        CurNId = EI.GetDstNId();
      } else {
        Flow[NextEId] -= MinAug;
        CurNId = EI.GetSrcNId();
      }
    }
  }
  return MaxFlow;
}

Here is the call graph for this function:

int TSnap::GetMaxFlowIntPR	(	PNEANet &	Net,
		const int &	SrcNId,
		const int &	SnkNId
	)

Returns the maximum integer valued flow in the network Net from source SrcNId to sink SnkNId.

Implements max flow using the Edmonds-Karp algorithm. http://en.wikipedia.org/wiki/Edmonds%E2%80%93Karp_algorithm Although the asymptotic run time of Edmonds-Karp is worse than that of Push Relabel, in practice Edmonds Karp works very well, especially if the network is sparse. Unless the degree of each node is on the order of the number of nodes, it is best to use Edmonds Karp over Push Relabel.

Definition at line 410 of file flow.cpp.

References TSnap::TPRManager::Capacity(), TSnap::TPRManager::Excess(), TSnap::TPRManager::Flow(), TSnap::TPRManager::GetMaxLabel(), TNEANet::TNodeI::GetOutDeg(), TNEANet::TNodeI::GetOutEId(), TNEANet::TNodeI::GetOutNId(), GlobalRelabel(), TSnap::TPRManager::HasActive(), IAssert, TSnap::TPRManager::IsActive(), TSnap::TPRManager::Label(), TSnap::TPRManager::PopActive(), TSnap::TPRManager::PushActive(), PushRelabel(), and TSnap::TPRManager::SetLabel().

                                                                         {
  IAssert(Net->IsNode(SrcNId));
  IAssert(Net->IsNode(SnkNId));
  if (SrcNId == SnkNId) { return 0; }

  TPRManager PRM(Net);
  int MaxLabel = PRM.GetMaxLabel();

  TNEANet::TNodeI SrcNI = Net->GetNI(SrcNId);
  for (int EdgeN = 0; EdgeN < SrcNI.GetOutDeg(); EdgeN++) {
    int EId = SrcNI.GetOutEId(EdgeN);
    int OutNId = SrcNI.GetOutNId(EdgeN);
    if (OutNId != SrcNId) {
      int Capacity = PRM.Capacity(EId);
      PRM.Flow(EId) = Capacity;
      PRM.Excess(OutNId) = Capacity;
    }
  }
  GlobalRelabel(Net, PRM, SrcNId, SnkNId);
  PRM.SetLabel(SrcNId, MaxLabel);
  int RelabelCount = 1;
  int GRRate = Net->GetNodes();
  while (PRM.HasActive()) {
    int NId = PRM.PopActive();
    const TNEANet::TNodeI &NI = Net->GetNI(NId);
    int PrevLabel = MaxLabel;
    while (PRM.Excess(NId) > 0 && PRM.Label(NId) <= PrevLabel) {
      PrevLabel = PRM.Label(NId);
      int NbrNId = PushRelabel(PRM, NId, NI);
      if (NbrNId != -1 && NbrNId != SnkNId && PRM.Excess(NbrNId) > 0 && !PRM.IsActive(NbrNId)) {
        PRM.PushActive(NbrNId);
      }
    }
    if (PRM.Excess(NId) > 0 && PRM.Label(NId) < MaxLabel) {
      PRM.PushActive(NId);
    }
    if (RelabelCount % GRRate == 0) { GlobalRelabel(Net, PRM, SrcNId, SnkNId); }
  }
  return PRM.Excess(SnkNId);
}

Here is the call graph for this function:

template<typename PGraph >

double TSnap::GetModularity	(	const PGraph &	G,
		const TIntV &	NIdV,
		int	GEdges = -1
	)

Computes Modularity score of a set of nodes NIdV in a graph G. The function runs much faster if the number of edges in graph G is given (GEdges parameter).

Definition at line 37 of file cmty.h.

References THashSet< TKey, THashFunc >::AddKey(), and TVec< TVal, TSizeTy >::Len().

Referenced by GetModularity().

                                                                         {
  if (GEdges == -1) { GEdges = Graph->GetEdges(); }
  double EdgesIn = 0.0, EEdgesIn = 0.0; // EdgesIn=2*number of edges inside the cluster, EEdgesIn=expected edges inside
  TIntSet NIdSet(NIdV.Len());
  for (int e = 0; e < NIdV.Len(); e++) { // edges inside
    NIdSet.AddKey(NIdV[e]); }
  for (int e1 = 0; e1 < NIdV.Len(); e1++) {
    typename PGraph::TObj::TNodeI NI = Graph->GetNI(NIdV[e1]);
    EEdgesIn += NI.GetOutDeg();
    for (int i = 0; i < NI.GetOutDeg(); i++) {
      if (NIdSet.IsKey(NI.GetOutNId(i))) { EdgesIn += 1; }
    }
  }
  EEdgesIn = EEdgesIn*EEdgesIn/(2.0*GEdges);
  if ((EdgesIn - EEdgesIn) == 0) { return 0; }
  else { return (EdgesIn - EEdgesIn) / (2.0*GEdges); } // modularity
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<typename PGraph >

double TSnap::GetModularity	(	const PGraph &	G,
		const TCnComV &	CmtyV,
		int	GEdges = -1
	)

Computes Modularity score of a set of communities (each community is defined by its member nodes) in a graph G. The function runs much faster if the number of edges in graph G is given (GEdges parameter).

Definition at line 56 of file cmty.h.

References GetModularity(), and TVec< TVal, TSizeTy >::Len().

                                                                        {
  if (GEdges == -1) { GEdges = G->GetEdges(); }
  double Modularity = 0;
  for (int c = 0; c < CmtyV.Len(); c++) {
    Modularity += GetModularity(G, CmtyV[c](), GEdges);
  }
  return Modularity;
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::GetMxBiCon

(

const PGraph &

Graph

)

Returns a graph representing the largest bi-connected component on an input Graph.

An undirected graph is bi-connected if by removing any single node does not disconnect the graph. http://en.wikipedia.org/wiki/Biconnected_component

Definition at line 486 of file cncom.h.

References TVec< TVal, TSizeTy >::Empty(), GetBiCon(), GetSubGraph(), and TVec< TVal, TSizeTy >::Len().

                                       {
  TCnComV CnComV;
  GetBiCon(TSnap::ConvertGraph<PUNGraph, PGraph>(Graph), CnComV);
  if (CnComV.Empty()) { return PGraph::TObj::New(); }
  int CcId = 0, MxSz = 0;
  for (int i = 0; i < CnComV.Len(); i++) {
    if (MxSz < CnComV[i].Len()) {
      MxSz=CnComV[i].Len();  CcId=i; }
  }
  if (CnComV[CcId].Len()==Graph->GetNodes()) { 
    return Graph; }
  else { 
    return TSnap::GetSubGraph(Graph, CnComV[CcId]()); 
  }
}

Here is the call graph for this function:

PUNGraph TSnap::GetMxBiCon	(	const PUNGraph &	Graph,
		const bool &	RenumberNodes = false
	)

Returns a graph representing the largest bi-connected component on an undirected Graph.

An undirected graph is bi-connected if by removing any single node does not disconnect the graph. http://en.wikipedia.org/wiki/Biconnected_component

Definition at line 126 of file cncom.cpp.

References TVec< TVal, TSizeTy >::Empty(), GetBiCon(), GetSubGraph(), and TVec< TVal, TSizeTy >::Len().

Referenced by TGStat::TakeBccStat().

                                                                      {
  TCnComV CnComV;
  GetBiCon(Graph, CnComV);
  if (CnComV.Empty()) { 
    return PUNGraph(); 
  }
  int CcId = 0, MxSz = 0;
  for (int i = 0; i < CnComV.Len(); i++) {
    if (MxSz < CnComV[i].Len()) {
      MxSz = CnComV[i].Len();  
      CcId=i; 
    }
  }
  return TSnap::GetSubGraph(Graph, CnComV[CcId](), RenumberNodes);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

int TSnap::GetMxDegNId

(

const PGraph &

Graph

)

Returns a randomly chosen node from all the nodes with the maximum degree.

Definition at line 143 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Clr(), EAssertR, TVec< TVal, TSizeTy >::Empty(), TRnd::GetUniDevInt(), TVec< TVal, TSizeTy >::Len(), and TInt::Rnd.

                                     {
  TIntV MxDegV;
  int MxDeg=-1;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (MxDeg < NI.GetDeg()) { MxDegV.Clr(); MxDeg = NI.GetDeg(); }
    if (MxDeg == NI.GetDeg()) { MxDegV.Add(NI.GetId()); }
  }
  EAssertR(! MxDegV.Empty(), "Input graph is empty!");
  return MxDegV[TInt::Rnd.GetUniDevInt(MxDegV.Len())];
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetMxInDegNId

(

const PGraph &

Graph

)

Returns a randomly chosen node from all the nodes with the maximum in-degree.

Definition at line 155 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Clr(), EAssertR, TVec< TVal, TSizeTy >::Empty(), TRnd::GetUniDevInt(), TVec< TVal, TSizeTy >::Len(), and TInt::Rnd.

                                       {
  TIntV MxDegV;
  int MxDeg=-1;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (MxDeg < NI.GetInDeg()) { MxDegV.Clr(); MxDeg = NI.GetInDeg(); }
    if (MxDeg == NI.GetInDeg()) { MxDegV.Add(NI.GetId()); }
  }
  EAssertR(! MxDegV.Empty(), "Input graph is empty!");
  return MxDegV[TInt::Rnd.GetUniDevInt(MxDegV.Len())];
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetMxOutDegNId

(

const PGraph &

Graph

)

Returns a randomly chosen node from all the nodes with the maximum out-degree.

Definition at line 167 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Clr(), EAssertR, TVec< TVal, TSizeTy >::Empty(), TRnd::GetUniDevInt(), TVec< TVal, TSizeTy >::Len(), and TInt::Rnd.

                                        {
  TIntV MxDegV;
  int MxDeg=-1;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (MxDeg < NI.GetOutDeg()) { MxDegV.Clr(); MxDeg = NI.GetOutDeg(); }
    if (MxDeg == NI.GetOutDeg()) { MxDegV.Add(NI.GetId()); }
  }
  EAssertR(! MxDegV.Empty(), "Input graph is empty!");
  return MxDegV[TInt::Rnd.GetUniDevInt(MxDegV.Len())];
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::GetMxScc

(

const PGraph &

Graph

)

Returns a graph representing the largest strongly connected component on an input Graph.

A directed graph is strongly connected if there exists a directed path from any vertex to any other vertex in the graph. See http://en.wikipedia.org/wiki/Strongly_connected_component

Definition at line 469 of file cncom.h.

References TVec< TVal, TSizeTy >::Empty(), GetSccs(), GetSubGraph(), and TVec< TVal, TSizeTy >::Len().

Referenced by TGStat::TakeSccStat().

                                     {
  TCnComV CnComV;
  GetSccs(Graph, CnComV);
  if (CnComV.Empty()) { return PGraph::TObj::New(); }
  int CcId = 0, MxSz = 0;
  for (int i = 0; i < CnComV.Len(); i++) {
    if (MxSz < CnComV[i].Len()) {
      MxSz=CnComV[i].Len();  CcId=i; }
  }
  if (CnComV[CcId].Len()==Graph->GetNodes()) { 
    return Graph; }
  else { 
    return TSnap::GetSubGraph(Graph, CnComV[CcId]()); 
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

double TSnap::GetMxSccSz

(

const PGraph &

Graph

)

Returns the fraction of nodes in the largest strongly connected component of a Graph.

Definition at line 444 of file cncom.h.

References GetSccs(), and TVec< TVal, TSizeTy >::Len().

Referenced by PrintInfo().

                                       {
  TCnComV CnComV;
  GetSccs(Graph, CnComV);
  if (Graph->GetNodes() == 0) { return 0; }
  else { return CnComV[0].Len() / double(Graph->GetNodes()); }
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

PGraph TSnap::GetMxWcc

(

const PGraph &

Graph

)

Returns a graph representing the largest weakly connected component on an input Graph.

A directed/undirected graph is connected if there exist an undirected path between any pair of nodes. See http://en.wikipedia.org/wiki/Connected_component_(graph_theory)

Definition at line 452 of file cncom.h.

References TVec< TVal, TSizeTy >::Empty(), GetSubGraph(), GetWccs(), and TVec< TVal, TSizeTy >::Len().

Referenced by main(), TKronMtx::PlotCmpGraphs(), TTimeNet::PlotEffDiam(), TTimeNENet::PlotEffDiam(), TTimeNet::PlotMissingPast(), TLocClustStat::Run(), and TGStat::TakeStat().

                                     {
  TCnComV CnComV;
  GetWccs(Graph, CnComV);
  if (CnComV.Empty()) { return PGraph::TObj::New(); }
  int CcId = 0, MxSz = 0;
  for (int i = 0; i < CnComV.Len(); i++) {
    if (MxSz < CnComV[i].Len()) {
      MxSz=CnComV[i].Len();  CcId=i; }
  }
  if (CnComV[CcId].Len()==Graph->GetNodes()) { 
    return Graph; }
  else { 
    return TSnap::GetSubGraph(Graph, CnComV[CcId]()); 
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

double TSnap::GetMxWccSz

(

const PGraph &

Graph

)

Returns the fraction of nodes in the largest weakly connected component of a Graph.

Definition at line 436 of file cncom.h.

References GetWccs(), and TVec< TVal, TSizeTy >::Len().

Referenced by PrintInfo().

                                       {
  TCnComV CnComV;
  GetWccs(Graph, CnComV);
  if (Graph->GetNodes() == 0) { return 0; }
  else { return CnComV[0].Len() / double(Graph->GetNodes()); }
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

double TSnap::GetNodeClustCf	(	const PGraph &	Graph,
		const int &	NId
	)

Returns clustering coefficient of a particular node.

Considers the graph as undirected.

Definition at line 168 of file triad.h.

References GetNodeTriads().

                                                           {
  int Open, Closed;
  GetNodeTriads(Graph, NId, Open, Closed);
  //const double Deg = Graph->GetNI(NId).GetDeg();
  return (Open+Closed)==0 ? 0 : double(Open)/double(Open+Closed);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetNodeClustCf	(	const PGraph &	Graph,
		TIntFltH &	NIdCCfH
	)

Computes clustering coefficient of each node of the Graph.

Considers the graph as undirected.

Parameters

DegToCCfV	Vector of pairs (degree, avg. clustering coefficient of nodes of that degree).
SampleNodes	If !=-1 then compute clustering coefficient only for a random sample of SampleNodes nodes. Useful for approximate but quick computations.

Definition at line 176 of file triad.h.

References THash< TKey, TDat, THashFunc >::AddDat(), THash< TKey, TDat, THashFunc >::Clr(), GetTriads(), and TVec< TVal, TSizeTy >::Len().

                                                            {
  TIntTrV NIdCOTriadV;
  GetTriads(Graph, NIdCOTriadV);
  NIdCCfH.Clr(false);
  for (int i = 0; i < NIdCOTriadV.Len(); i++) {
    const int D = NIdCOTriadV[i].Val2()+NIdCOTriadV[i].Val3();
    const double CCf = D!=0 ? NIdCOTriadV[i].Val2() / double(D) : 0.0;
    NIdCCfH.AddDat(NIdCOTriadV[i].Val1, CCf);
  }
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetNodeEcc	(	const PGraph &	Graph,
		const int &	NId,
		const bool &	IsDir = false
	)

Returns node Eccentricity, the largest shortest-path distance from the node NId to any other node in the Graph.

Parameters

IsDir

false: ignore edge directions and consider edges as undirected (in case they are directed).

Definition at line 53 of file centr.h.

References TBreathFS< PGraph >::DoBfs(), THash< TKey, TDat, THashFunc >::Len(), TInt::Mx, and TBreathFS< PGraph >::NIdDistH.

                                                                       {
  int NodeEcc;
  int Dist;
  TBreathFS<PGraph> BFS(Graph);
  // get shortest paths to all the nodes
  BFS.DoBfs(NId, true, ! IsDir, -1, TInt::Mx);

  NodeEcc = 0;
  // find the largest value
  for (int i = 0; i < BFS.NIdDistH.Len(); i++) {
    Dist = BFS.NIdDistH[i];
    if (Dist > NodeEcc) {
      NodeEcc = Dist;
    }
  }
  return NodeEcc;
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetNodeInDegV	(	const PGraph &	Graph,
		TIntPrV &	NIdInDegV
	)

Returns a vector of pairs (node id, node in-degree)

Definition at line 263 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), and TVec< TVal, TSizeTy >::Reserve().

                                                            {
  NIdInDegV.Reserve(Graph->GetNodes(), 0);
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    NIdInDegV.Add(TIntPr(NI.GetId(), NI.GetInDeg()));
  }
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetNodeOutDegV	(	const PGraph &	Graph,
		TIntPrV &	NIdOutDegV
	)

Returns a vector of pairs (node id, node out-degree)

Definition at line 271 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), and TVec< TVal, TSizeTy >::Reserve().

                                                              {
  NIdOutDegV.Reserve(Graph->GetNodes(), 0);
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    NIdOutDegV.Add(TIntPr(NI.GetId(), NI.GetOutDeg()));
  }
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetNodesAtHop	(	const PGraph &	Graph,
		const int &	StartNId,
		const int &	Hop,
		TIntV &	NIdV,
		const bool &	IsDir = false
	)

Finds IDs of all nodes that are at distance Hop from node StartNId.

false: ignore edge directions and consider edges/paths as undirected (in case they are directed).

Definition at line 229 of file bfsdfs.h.

References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Clr(), TBreathFS< PGraph >::DoBfs(), THash< TKey, TDat, THashFunc >::GetKey(), THash< TKey, TDat, THashFunc >::Len(), TVec< TVal, TSizeTy >::Len(), and TBreathFS< PGraph >::NIdDistH.

                                                                                                            {
  TBreathFS<PGraph> BFS(Graph);
  BFS.DoBfs(StartNId, true, !IsDir, -1, Hop);
  NIdV.Clr(false);
  for (int i = 0; i < BFS.NIdDistH.Len(); i++) {
    if (BFS.NIdDistH[i] == Hop) {
      NIdV.Add(BFS.NIdDistH.GetKey(i)); }
  }
  return NIdV.Len();
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetNodesAtHops	(	const PGraph &	Graph,
		const int &	StartNId,
		TIntPrV &	HopCntV,
		const bool &	IsDir = false
	)

Returns the number of nodes at each hop distance from the starting node StartNId.

false: ignore edge directions and consider edges/paths as undirected (in case they are directed).

Definition at line 241 of file bfsdfs.h.

References THash< TKey, TDat, THashFunc >::AddDat(), TBreathFS< PGraph >::DoBfs(), THash< TKey, TDat, THashFunc >::GetKeyDatPrV(), THash< TKey, TDat, THashFunc >::Len(), TVec< TVal, TSizeTy >::Len(), TInt::Mx, TBreathFS< PGraph >::NIdDistH, and TVec< TVal, TSizeTy >::Sort().

                                                                                                  {
  TBreathFS<PGraph> BFS(Graph);
  BFS.DoBfs(StartNId, true, !IsDir, -1, TInt::Mx);
  TIntH HopCntH;
  for (int i = 0; i < BFS.NIdDistH.Len(); i++) {
    HopCntH.AddDat(BFS.NIdDistH[i]) += 1;
  }
  HopCntH.GetKeyDatPrV(HopCntV);
  HopCntV.Sort();
  return HopCntV.Len();
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetNodeTriads	(	const PGraph &	Graph,
		const int &	NId
	)

Returns the number of undirected triads a node NId participates in.

Considers the graph as undirected.

Parameters

Graph	Input graph
NId	Input node

Definition at line 295 of file triad.h.

Referenced by GetNodeClustCf(), and GetTriadParticip().

                                                       {
  int ClosedTriads=0, OpenTriads=0;
  return GetNodeTriads(Graph, NId, ClosedTriads, OpenTriads);
}

Here is the caller graph for this function:

template<class PGraph >

int TSnap::GetNodeTriads	(	const PGraph &	Graph,
		const int &	NId,
		int &	ClosedNTriadsX,
		int &	OpenNTriadsX
	)

Returns number of Open and Closed triads a node NId participates in.

Considers the graph as undirected.

Parameters

Graph	Input graph
NId	Input node
ClosedNTriadsX	On return contains the number of closed triads
OpenNTriadsX	On return contains the number of open triads

Definition at line 302 of file triad.h.

References THashSet< TKey, THashFunc >::AddKey(), and gfDirected.

                                                                                           {
  const typename PGraph::TObj::TNodeI NI = Graph->GetNI(NId);
  ClosedTriads=0;  OpenTriads=0;
  if (NI.GetDeg() < 2) { return 0; }
  // find neighborhood
  TIntSet NbrSet(NI.GetDeg());
  for (int e = 0; e < NI.GetOutDeg(); e++) {
    if (NI.GetOutNId(e) != NI.GetId()) { // exclude self edges
      NbrSet.AddKey(NI.GetOutNId(e)); }
  }
  if (Graph->HasFlag(gfDirected)) {
    for (int e = 0; e < NI.GetInDeg(); e++) {
      if (NI.GetInNId(e) != NI.GetId()) { // exclude self edges
        NbrSet.AddKey(NI.GetInNId(e)); }
    }
  }
  // count connected neighbors
  for (int srcNbr = 0; srcNbr < NbrSet.Len(); srcNbr++) {
    const typename PGraph::TObj::TNodeI SrcNode = Graph->GetNI(NbrSet.GetKey(srcNbr));
    for (int dstNbr = srcNbr+1; dstNbr < NbrSet.Len(); dstNbr++) {
      const int dstNId = NbrSet.GetKey(dstNbr);
      if (SrcNode.IsNbrNId(dstNId)) { ClosedTriads++; }
      else { OpenTriads++; }
    }
  }
  return ClosedTriads;
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetNodeTriads	(	const PGraph &	Graph,
		const int &	NId,
		const TIntSet &	GroupSet,
		int &	InGroupEdgesX,
		int &	InOutGroupEdgesX,
		int &	OutGroupEdgesX
	)

Returns the number of triads between a node NId and a subset of its neighbors GroupSet.

Considers the graph as undirected.

Parameters

Graph	Input graph
NId	Input node
GroupSet	Input set with node neighbors
InGroupEdgesX	On return contains the number of triads (NId, G1, G2), where G1 and G2 are in GroupSet
InOutGroupEdgesX	On return contains the number of triads (NId, G1, O1), where G1 is in GroupSet and O1 not in GroupSet
OutGroupEdgesX	On return contains the number of triads (NId, O1, O2), where O1 and O2 are not in GroupSet

Definition at line 335 of file triad.h.

References THashSet< TKey, THashFunc >::AddKey(), gfDirected, and THashSet< TKey, THashFunc >::IsKey().

                                                                                                                                             {
  const typename PGraph::TObj::TNodeI NI = Graph->GetNI(NId);
  const bool IsDir = Graph->HasFlag(gfDirected);
  InGroupEdges=0;  InOutGroupEdges=0;  OutGroupEdges=0;
  if (NI.GetDeg() < 2) { return 0; }
  // find neighborhood
  TIntSet NbrSet(NI.GetDeg());
  for (int e = 0; e < NI.GetOutDeg(); e++) {
    if (NI.GetOutNId(e) != NI.GetId()) { // exclude self edges
      NbrSet.AddKey(NI.GetOutNId(e)); }
  }
  if (IsDir) {
    for (int e = 0; e < NI.GetInDeg(); e++) {
      if (NI.GetInNId(e) != NI.GetId()) {
        NbrSet.AddKey(NI.GetInNId(e)); }
    }
  }
  // count connected neighbors
  for (int srcNbr = 0; srcNbr < NbrSet.Len(); srcNbr++) {
    const int NbrId = NbrSet.GetKey(srcNbr);
    const bool NbrIn = GroupSet.IsKey(NbrId);
    const typename PGraph::TObj::TNodeI SrcNode = Graph->GetNI(NbrId);
    for (int dstNbr = srcNbr+1; dstNbr < NbrSet.Len(); dstNbr++) {
      const int DstNId = NbrSet.GetKey(dstNbr);
      if (SrcNode.IsNbrNId(DstNId)) { // triad (NId, NbrId, DstNid)
        bool DstIn = GroupSet.IsKey(DstNId);
        if (NbrIn && DstIn) { InGroupEdges++; }
        else if (NbrIn || DstIn) { InOutGroupEdges++; }
        else { OutGroupEdges++; }
      }
    }
  }
  return InGroupEdges;
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetNodeWcc	(	const PGraph &	Graph,
		const int &	NId,
		TIntV &	CnCom
	)

Returns (via output parameter CnCom) all nodes that are in the same connected component as node NId.

Definition at line 277 of file cncom.h.

References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Gen(), gfDirected, HasGraphFlag, and TSnapQueue< TVal >::Push().

Referenced by TSnap::TSnapDetail::CmtyGirvanNewmanStep().

                                                                   {
  typename PGraph::TObj::TNodeI NI;
  THashSet<TInt> VisitedNId(Graph->GetNodes()+1);
  TSnapQueue<int> NIdQ(Graph->GetNodes()+1);
  VisitedNId.AddKey(NId);
  NIdQ.Push(NId);
  while (! NIdQ.Empty()) {
    const typename PGraph::TObj::TNodeI Node = Graph->GetNI(NIdQ.Top());  NIdQ.Pop();
    if (HasGraphFlag(typename PGraph::TObj, gfDirected)) {
      for (int e = 0; e < Node.GetInDeg(); e++) {
        const int InNId = Node.GetInNId(e);
        if (! VisitedNId.IsKey(InNId)) {
          NIdQ.Push(InNId);  VisitedNId.AddKey(InNId); }
      }
    }
    for (int e = 0; e < Node.GetOutDeg(); e++) {
      const int OutNId = Node.GetOutNId(e);
      if (! VisitedNId.IsKey(OutNId)) {
        NIdQ.Push(OutNId);  VisitedNId.AddKey(OutNId); }
    }
  }
  CnCom.Gen(VisitedNId.Len(), 0);
  for (int i = 0; i < VisitedNId.Len(); i++) {
    CnCom.Add(VisitedNId.GetKey(i));
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::GetOutDegCnt	(	const PGraph &	Graph,
		TIntPrV &	DegToCntV
	)

Returns an out-degree histogram: a set of pairs (out-degree, number of nodes of such out-degree)

Definition at line 201 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TVec< TVal, TSizeTy >::Gen(), THash< TKey, TDat, THashFunc >::GetKey(), THash< TKey, TDat, THashFunc >::Len(), and TVec< TVal, TSizeTy >::Sort().

Referenced by PlotOutDegDistr(), and TGStat::TakeDegDistr().

                                                           {
  TIntH DegToCntH;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    DegToCntH.AddDat(NI.GetOutDeg())++; }
  DegToCntV.Gen(DegToCntH.Len(), 0);
  for (int i = 0; i < DegToCntH.Len(); i++) {
    DegToCntV.Add(TIntPr(DegToCntH.GetKey(i), DegToCntH[i])); }
  DegToCntV.Sort();
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::GetOutDegCnt	(	const PGraph &	Graph,
		TFltPrV &	DegToCntV
	)

Returns an out-degree histogram: a set of pairs (out-degree, number of nodes of such out-degree)

Definition at line 212 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TVec< TVal, TSizeTy >::Gen(), THash< TKey, TDat, THashFunc >::GetKey(), THash< TKey, TDat, THashFunc >::Len(), and TVec< TVal, TSizeTy >::Sort().

                                                           {
  TIntH DegToCntH;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    DegToCntH.AddDat(NI.GetOutDeg())++; }
  DegToCntV.Gen(DegToCntH.Len(), 0);
  for (int i = 0; i < DegToCntH.Len(); i++) {
    DegToCntV.Add(TFltPr(DegToCntH.GetKey(i).Val, DegToCntH[i].Val)); }
  DegToCntV.Sort();
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetPageRank	(	const PGraph &	Graph,
		TIntFltH &	PRankH,
		const double &	C = 0.85,
		const double &	Eps = 1e-4,
		const int &	MaxIter = 100
	)

PageRank For more info see: http://en.wikipedia.org/wiki/PageRank

Definition at line 75 of file centr.h.

References THash< TKey, TDat, THashFunc >::AddDat(), THash< TKey, TDat, THashFunc >::Gen(), THash< TKey, TDat, THashFunc >::GetDat(), THash< TKey, TDat, THashFunc >::Len(), and TVec< TVal, TSizeTy >::Len().

                                                                                                                {
  const int NNodes = Graph->GetNodes();
  //const double OneOver = 1.0/double(NNodes);
  PRankH.Gen(NNodes);
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    PRankH.AddDat(NI.GetId(), 1.0/NNodes);
    //IAssert(NI.GetId() == PRankH.GetKey(PRankH.Len()-1));
  }
  TFltV TmpV(NNodes);
  for (int iter = 0; iter < MaxIter; iter++) {
    int j = 0;
    for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++, j++) {
      TmpV[j] = 0;
      for (int e = 0; e < NI.GetInDeg(); e++) {
        const int InNId = NI.GetInNId(e);
        const int OutDeg = Graph->GetNI(InNId).GetOutDeg();
        if (OutDeg > 0) {
          TmpV[j] += PRankH.GetDat(InNId) / OutDeg; }
      }
      TmpV[j] =  C*TmpV[j]; // Berkhin (the correct way of doing it)
      //TmpV[j] =  C*TmpV[j] + (1.0-C)*OneOver; // iGraph
    }
    double diff=0, sum=0, NewVal;
    for (int i = 0; i < TmpV.Len(); i++) { sum += TmpV[i]; }
    const double Leaked = (1.0-sum) / double(NNodes);
    for (int i = 0; i < PRankH.Len(); i++) { // re-instert leaked PageRank
      NewVal = TmpV[i] + Leaked; // Berkhin
      //NewVal = TmpV[i] / sum;  // iGraph
      diff += fabs(NewVal-PRankH[i]);
      PRankH[i] = NewVal;
    }
    if (diff < Eps) { break; }
  }
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::GetRndESubGraph	(	const PGraph &	Graph,
		const int &	NEdges
	)

Returns a random subgraph of graph Graph with NEdges edges.

Randomly selects NEdges edges from the input graph and returns a subgraph on those edges.

Definition at line 452 of file subgraph.h.

References TVec< TVal, TSizeTy >::Add(), CAssert, GetESubGraph(), gfMultiGraph, HasGraphFlag, IAssert, and TInt::Rnd.

                                                               {
  CAssert(! HasGraphFlag(typename PGraph::TObj, gfMultiGraph));
  TIntPrV EdgeV(Graph->GetEdges(), 0);
  for (typename PGraph::TObj::TEdgeI EI = Graph->BegEI(); EI < Graph->EndEI(); EI++) {
    EdgeV.Add(TIntPr(EI.GetSrcNId(), EI.GetDstNId()));
  }
  EdgeV.Shuffle(TInt::Rnd);
  EdgeV.Del(NEdges, EdgeV.Len()-1);
  IAssert(EdgeV.Len() == NEdges);
  return GetESubGraph(Graph, EdgeV);
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::GetRndSubGraph	(	const PGraph &	Graph,
		const int &	NNodes
	)

Returns an induced random subgraph of graph Graph with NNodes nodes.

Randomly selects NNodes nodes from the input graph and returns an induced graph on those nodes.

Definition at line 441 of file subgraph.h.

References TVec< TVal, TSizeTy >::Del(), GetSubGraph(), IAssert, TVec< TVal, TSizeTy >::Len(), TInt::Rnd, and TVec< TVal, TSizeTy >::Shuffle().

                                                              {
  IAssert(NNodes <= Graph->GetNodes());
  TIntV NIdV;
  Graph->GetNIdV(NIdV);
  NIdV.Shuffle(TInt::Rnd);
  NIdV.Del(NNodes, NIdV.Len()-1);
  IAssert(NIdV.Len() == NNodes);
  return GetSubGraph(Graph, NIdV);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetSccs	(	const PGraph &	Graph,
		TCnComV &	CnComV
	)

Returns all strongly connected components in a Graph.

Parameters

CnComV

is a vector of connected components. Each component is defined by the IDs of its member nodes.

Definition at line 428 of file cncom.h.

References TSccVisitor< PGraph, OnlyCount >::CnComV, TCnCom::GetDfsVisitor(), and TVec< TVal, TSizeTy >::Sort().

Referenced by GetMxScc(), and GetMxSccSz().

                                                   {
  TSccVisitor<PGraph, false> Visitor(Graph);
  TCnCom::GetDfsVisitor(Graph, Visitor);
  CnComV = Visitor.CnComV;
  CnComV.Sort(false);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::GetSccSzCnt	(	const PGraph &	Graph,
		TIntPrV &	SccSzCnt
	)

Returns a distribution of strongly connected component sizes.

Parameters

SccSzCnt

returns a set of pairs (number of nodes in the component, number of such components)

Definition at line 420 of file cncom.h.

References TCnCom::GetDfsVisitor(), THash< TKey, TDat, THashFunc >::GetKeyDatPrV(), TSccVisitor< PGraph, OnlyCount >::SccCntH, and TVec< TVal, TSizeTy >::Sort().

Referenced by PlotSccDistr(), and TGStat::TakeConnComp().

                                                         {
  TSccVisitor<PGraph, true> Visitor(Graph);
  TCnCom::GetDfsVisitor(Graph, Visitor);
  Visitor.SccCntH.GetKeyDatPrV(SccSzCnt);
  SccSzCnt.Sort(true);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

int TSnap::GetShortPath	(	const PGraph &	Graph,
		const int &	SrcNId,
		const int &	DstNId,
		const bool &	IsDir = false
	)

Returns the length of the shortest path from node SrcNId to node DstNId.

Parameters

IsDir

false: ignore edge directions and consider edges/paths as undirected (in case they are directed).

Definition at line 263 of file bfsdfs.h.

References TBreathFS< PGraph >::DoBfs(), TBreathFS< PGraph >::GetHops(), and TInt::Mx.

                                                                                               {
  TBreathFS<PGraph> BFS(Graph);
  BFS.DoBfs(SrcNId, true, ! IsDir, DstNId, TInt::Mx);
  return BFS.GetHops(SrcNId, DstNId);
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetShortPath	(	const PGraph &	Graph,
		const int &	SrcNId,
		TIntH &	NIdToDistH,
		const bool &	IsDir = false,
		const int &	MaxDist = TInt::Mx
	)

Returns the length of the shortest path from node SrcNId to all other nodes in the network.

Parameters

IsDir	false: ignore edge directions and consider edges/paths as undirected (in case they are directed).
MaxDist	Maximum number of hops that BFS expands to. This is helpful for speeding-up the code if one in interested only in nodes less than MaxDist away from SrcNId.
NIdToDistH	Maps node ID to shortest path distance. NIdToDistH contains only nodes that are reachable from SrcNId.

Definition at line 254 of file bfsdfs.h.

References THash< TKey, TDat, THashFunc >::Clr(), TBreathFS< PGraph >::DoBfs(), THash< TKey, TDat, THashFunc >::Len(), TBreathFS< PGraph >::NIdDistH, and THash< TKey, TDat, THashFunc >::Swap().

                                                                                                                   {
  TBreathFS<PGraph> BFS(Graph);
  BFS.DoBfs(SrcNId, true, ! IsDir, -1, MaxDist);
  NIdToDistH.Clr();
  NIdToDistH.Swap(BFS.NIdDistH);
  return NIdToDistH[NIdToDistH.Len()-1];
}

Here is the call graph for this function:

void TSnap::GetSngVals	(	const PNGraph &	Graph,
		const int &	SngVals,
		TFltV &	SngValV
	)

Computes largest SngVals singular values of the adjacency matrix representing a directed Graph.

Definition at line 175 of file gsvd.cpp.

References THash< TKey, TDat, THashFunc >::AddKey(), TVVec< TVal >::At(), TNGraph::BegNI(), TNGraph::EndNI(), TNGraph::GetEdges(), THash< TKey, TDat, THashFunc >::GetKeyId(), TNGraph::GetNodes(), IAssert, TSparseSVD::LanczosSVD(), TVec< TVal, TSizeTy >::Len(), TSparseSVD::SimpleLanczosSVD(), TVec< TVal, TSizeTy >::Sort(), ssotFull, and TSvd::Svd1Based().

Referenced by TKroneckerLL::GradDescentConvergence(), PlotSngValDistr(), PlotSngValRank(), and TGStat::TakeSpectral().

                                                                          {
  const int Nodes = Graph->GetNodes();
  IAssert(SngVals > 0);
  if (Nodes < 100) {
    // perform full SVD
    TFltVV AdjMtx(Nodes+1, Nodes+1);
    TFltVV LSingV, RSingV;
    TIntH NodeIdH;
    // create adjecency matrix
    for (TNGraph::TNodeI NodeI = Graph->BegNI(); NodeI < Graph->EndNI(); NodeI++) {
      NodeIdH.AddKey(NodeI.GetId()); }
    for (TNGraph::TNodeI NodeI = Graph->BegNI(); NodeI < Graph->EndNI(); NodeI++) {
      const int NodeId = NodeIdH.GetKeyId(NodeI.GetId()) + 1;
      for (int e = 0; e < NodeI.GetOutDeg(); e++) {
        const int DstNId = NodeIdH.GetKeyId(NodeI.GetOutNId(e)) + 1;  // no self edges
        if (NodeId != DstNId) AdjMtx.At(NodeId, DstNId) = 1;
      }
    }
    try { // can fail to converge but results seem to be good
      TSvd::Svd1Based(AdjMtx, LSingV, SngValV, RSingV); }
    catch(...) {
      printf("\n***No SVD convergence: G(%d, %d)\n", Nodes, Graph->GetEdges()); }
  } else {
    // Lanczos
    TNGraphMtx GraphMtx(Graph);
    int CalcVals = int(2*SngVals);
    //if (CalcVals > Nodes) { CalcVals = int(2*Nodes); }
    //if (CalcVals > Nodes) { CalcVals = Nodes; }
    //while (SngValV.Len() < SngVals && CalcVals < 10*SngVals) {
    try {
      if (SngVals > 4) { 
        TSparseSVD::SimpleLanczosSVD(GraphMtx, 2*SngVals, SngValV, false); }
      else { TFltVV LSingV, RSingV;  // this is much more precise, but also much slower
        TSparseSVD::LanczosSVD(GraphMtx, SngVals, 3*SngVals, ssotFull, SngValV, LSingV, RSingV); }
    }
    catch(...) {
      printf("\n  ***EXCEPTION:  TRIED %d GOT %d values** \n", 2*SngVals, SngValV.Len()); }
    if (SngValV.Len() < SngVals) {
      printf("  ***TRIED %d GOT %d values** \n", CalcVals, SngValV.Len()); }
    //  CalcVals += SngVals;
    //}
  }
  SngValV.Sort(false);
  //if (SngValV.Len() > SngVals) {
  //  SngValV.Del(SngVals, SngValV.Len()-1); }
  //else {
  //  while (SngValV.Len() < SngVals) SngValV.Add(1e-6); }
  //IAssert(SngValV.Len() == SngVals);
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSnap::GetSngVec	(	const PNGraph &	Graph,
		TFltV &	LeftSV,
		TFltV &	RightSV
	)

Computes the leading left and right singular vector of the adjacency matrix representing a directed Graph.

Definition at line 225 of file gsvd.cpp.

References THash< TKey, TDat, THashFunc >::AddKey(), TVVec< TVal >::At(), TNGraph::BegNI(), TNGraph::EndNI(), TVVec< TVal >::GetCol(), TNGraph::GetEdges(), THash< TKey, TDat, THashFunc >::GetKeyId(), TNGraph::GetNodes(), IsAllValVNeg(), TSparseSVD::LanczosSVD(), TVec< TVal, TSizeTy >::Len(), TFlt::Mn, ssotFull, and TSvd::Svd1Based().

Referenced by PlotSngVec(), and TGStat::TakeSpectral().

                                                                    {
  const int Nodes = Graph->GetNodes();
  TFltVV LSingV, RSingV;
  TFltV SngValV;
  if (Nodes < 500) {
    // perform full SVD
    TFltVV AdjMtx(Nodes+1, Nodes+1);
    TIntH NodeIdH;
    // create adjecency matrix
    for (TNGraph::TNodeI NodeI = Graph->BegNI(); NodeI < Graph->EndNI(); NodeI++) {
      NodeIdH.AddKey(NodeI.GetId()); }
    for (TNGraph::TNodeI NodeI = Graph->BegNI(); NodeI < Graph->EndNI(); NodeI++) {
      const int NodeId = NodeIdH.GetKeyId(NodeI.GetId()) + 1;
      for (int e = 0; e < NodeI.GetOutDeg(); e++) {
        const int DstNId = NodeIdH.GetKeyId(NodeI.GetOutNId(e)) + 1;  // no self edges
        if (NodeId != DstNId) AdjMtx.At(NodeId, DstNId) = 1;
      }
    }
    try { // can fail to converge but results seem to be good
      TSvd::Svd1Based(AdjMtx, LSingV, SngValV, RSingV); }
    catch(...) {
      printf("\n***No SVD convergence: G(%d, %d)\n", Nodes, Graph->GetEdges()); }
  } else { // Lanczos
    TNGraphMtx GraphMtx(Graph);
    TSparseSVD::LanczosSVD(GraphMtx, 1, 8, ssotFull, SngValV, LSingV, RSingV);
  }
  TFlt MxSngVal = TFlt::Mn;
  int ValN = 0;
  for (int i = 0; i < SngValV.Len(); i++) {
    if (MxSngVal < SngValV[i]) { MxSngVal = SngValV[i]; ValN = i; } }
  LSingV.GetCol(ValN, LeftSV);
  RSingV.GetCol(ValN, RightSV);
  IsAllValVNeg(LeftSV, true);
  IsAllValVNeg(RightSV, true);
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSnap::GetSngVec	(	const PNGraph &	Graph,
		const int &	SngVecs,
		TFltV &	SngValV,
		TVec< TFltV > &	LeftSV,
		TVec< TFltV > &	RightSV
	)

Computes the singular values and left and right singular vectors of the adjacency matrix representing a directed Graph.

Parameters

SngVecs

Number of singular values/vectors to compute.

Definition at line 261 of file gsvd.cpp.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddKey(), TVVec< TVal >::At(), TNGraph::BegNI(), TVec< TVal, TSizeTy >::Clr(), TNGraph::EndNI(), TVVec< TVal >::GetCol(), TNGraph::GetEdges(), THash< TKey, TDat, THashFunc >::GetKeyId(), TNGraph::GetNodes(), IsAllValVNeg(), TSparseSVD::LanczosSVD(), TVec< TVal, TSizeTy >::Last(), TVec< TVal, TSizeTy >::Len(), TVec< TVal, TSizeTy >::Sort(), ssotFull, and TSvd::Svd1Based().

                                                                                                                    {
  const int Nodes = Graph->GetNodes();
  SngValV.Clr();
  LeftSV.Clr();
  RightSV.Clr();
  TFltVV LSingV, RSingV;
  if (Nodes < 100) {
    // perform full SVD
    TFltVV AdjMtx(Nodes+1, Nodes+1);
    TIntH NodeIdH;
    // create adjecency matrix (1-based)
    for (TNGraph::TNodeI NodeI = Graph->BegNI(); NodeI < Graph->EndNI(); NodeI++) {
      NodeIdH.AddKey(NodeI.GetId()); }
    for (TNGraph::TNodeI NodeI = Graph->BegNI(); NodeI < Graph->EndNI(); NodeI++) {
      const int NodeId = NodeIdH.GetKeyId(NodeI.GetId())+1;
      for (int e = 0; e < NodeI.GetOutDeg(); e++) {
        const int DstNId = NodeIdH.GetKeyId(NodeI.GetOutNId(e))+1;  // no self edges
        if (NodeId != DstNId) AdjMtx.At(NodeId, DstNId) = 1;
      }
    }
    try { // can fail to converge but results seem to be good
      TSvd::Svd1Based(AdjMtx, LSingV, SngValV, RSingV);
    } catch(...) {
      printf("\n***No SVD convergence: G(%d, %d)\n", Nodes, Graph->GetEdges()); 
    }
  } else { // Lanczos
    TNGraphMtx GraphMtx(Graph);
    TSparseSVD::LanczosSVD(GraphMtx, SngVecs, 2*SngVecs, ssotFull, SngValV, LSingV, RSingV);
    //TGAlg::SaveFullMtx(Graph, "adj_mtx.txt");
    //TLAMisc::DumpTFltVVMjrSubMtrx(LSingV, LSingV.GetRows(), LSingV.GetCols(), "LSingV2.txt"); // save MTX
  }
  TFltIntPrV SngValIdV;
  for (int i = 0; i < SngValV.Len(); i++) {
    SngValIdV.Add(TFltIntPr(SngValV[i], i)); 
  }
  SngValIdV.Sort(false);
  SngValV.Sort(false);
  for (int v = 0; v < SngValIdV.Len(); v++) { 
    LeftSV.Add();
    LSingV.GetCol(SngValIdV[v].Val2, LeftSV.Last());
    RightSV.Add();
    RSingV.GetCol(SngValIdV[v].Val2, RightSV.Last());
  }
  IsAllValVNeg(LeftSV[0], true);
  IsAllValVNeg(RightSV[0], true);
}

Here is the call graph for this function:

PUNGraph TSnap::GetSubGraph	(	const PUNGraph &	Graph,
		const TIntV &	NIdV,
		const bool &	RenumberNodes = false
	)

Returns an induced subgraph of an undirected graph Graph with NIdV nodes with an optional node renumbering.

The resulting subgraph contains all the nodes from Graph, which have node IDs in the NIdV vector and all the edges with both nodes in NIdV. Parameter RenumberNodes determines, whether the node IDs are preserved or not. If RenumberNodes is false, then nodes in the resulting subgraph have the same node IDs as nodes in Graph. If RenumberNodes is true, then nodes in the resulting subgraph are renumbered sequentially from 0 to N-1. By default, the nodes are not renumbered.

Definition at line 7 of file subgraph.cpp.

References TUNGraph::AddEdge(), THashSet< TKey, THashFunc >::AddKey(), TUNGraph::AddNode(), TUNGraph::TNodeI::GetOutDeg(), TUNGraph::TNodeI::GetOutNId(), TVec< TVal, TSizeTy >::Len(), TUNGraph::New(), and TUNGraph::Reserve().

Referenced by TCodaAnalyzer::Draw2ModeCommunity(), TLocClust::DrawWhiskers(), TKCore< PGraph >::GetCoreG(), GetKCore(), GetMxBiCon(), GetMxScc(), GetMxWcc(), GetRndSubGraph(), TTimeNet::PlotCCfOverTm(), TTimeNet::PlotMedianDegOverTm(), TTimeNet::PlotMissingPast(), TLocClustStat::PlotPhiInOut(), TAGMFast::SetGraph(), TCoda::SetGraph(), TKroneckerLL::SetGraph(), TCesna::SetGraph(), and TMAGFitBern::SetGraph().

                                                                                          {
  //if (! RenumberNodes) { return TSnap::GetSubGraph(Graph, NIdV); }
  PUNGraph NewGraphPt = TUNGraph::New();
  TUNGraph& NewGraph = *NewGraphPt;
  NewGraph.Reserve(NIdV.Len(), -1);
  TIntSet NIdSet(NIdV.Len());
  for (int n = 0; n < NIdV.Len(); n++) {
    if (Graph->IsNode(NIdV[n])) {
      NIdSet.AddKey(NIdV[n]);
      if (! RenumberNodes) { NewGraph.AddNode(NIdV[n]); }
      else { NewGraph.AddNode(NIdSet.GetKeyId(NIdV[n])); }
    }
  }
  if (! RenumberNodes) {
    for (int n = 0; n < NIdSet.Len(); n++) {
      const int SrcNId = NIdSet[n];
      const TUNGraph::TNodeI NI = Graph->GetNI(SrcNId);
      for (int edge = 0; edge < NI.GetOutDeg(); edge++) {
        const int OutNId = NI.GetOutNId(edge);
        if (NIdSet.IsKey(OutNId)) {
          NewGraph.AddEdge(SrcNId, OutNId); }
      }
    }
  } else {
    for (int n = 0; n < NIdSet.Len(); n++) {
      const int SrcNId = NIdSet[n];
      const TUNGraph::TNodeI NI = Graph->GetNI(SrcNId);
      for (int edge = 0; edge < NI.GetOutDeg(); edge++) {
        const int OutNId = NI.GetOutNId(edge);
        if (NIdSet.IsKey(OutNId)) {
          NewGraph.AddEdge(NIdSet.GetKeyId(SrcNId), NIdSet.GetKeyId(OutNId)); }
      }
    }
  }
  return NewGraphPt;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

PGraph TSnap::GetSubGraph	(	const PGraph &	Graph,
		const TIntV &	NIdV
	)

Returns an induced subgraph of graph Graph with NIdV nodes.

The resulting subgraph contains all the nodes from Graph, which have node IDs in the NIdV vector and all the edges with both nodes in NIdV. Node IDs are preserved. Nodes in the resulting subgraph have the same node IDs as nodes in Graph.

Definition at line 200 of file subgraph.h.

                                                           {
  return TSnapDetail::TGetSubGraph<PGraph, HasGraphFlag(typename PGraph::TObj, gfMultiGraph)>
    ::Do(Graph, NIdV);
}

PNGraph TSnap::GetSubGraph	(	const PNGraph &	Graph,
		const TIntV &	NIdV,
		const bool &	RenumberNodes
	)

Definition at line 45 of file subgraph.cpp.

References TNGraph::AddEdge(), THashSet< TKey, THashFunc >::AddKey(), TNGraph::AddNode(), TNGraph::GetNI(), TNGraph::TNodeI::GetOutDeg(), TNGraph::TNodeI::GetOutNId(), TNGraph::IsNode(), TVec< TVal, TSizeTy >::Len(), TNGraph::New(), and TNGraph::Reserve().

                                                                                        {
  //if (! RenumberNodes) { return TSnap::GetSubGraph(Graph, NIdV); }
  PNGraph NewGraphPt = TNGraph::New();
  TNGraph& NewGraph = *NewGraphPt;
  NewGraph.Reserve(NIdV.Len(), -1);
  TIntSet NIdSet(NIdV.Len());
  for (int n = 0; n < NIdV.Len(); n++) {
    if (Graph->IsNode(NIdV[n])) {
      NIdSet.AddKey(NIdV[n]);
      if (! RenumberNodes) { NewGraph.AddNode(NIdV[n]); }
      else { NewGraph.AddNode(NIdSet.GetKeyId(NIdV[n])); }
    }
  }
  if (! RenumberNodes) {
    for (int n = 0; n < NIdSet.Len(); n++) {
      const int SrcNId = NIdSet[n];
      const TNGraph::TNodeI NI = Graph->GetNI(SrcNId);
      for (int edge = 0; edge < NI.GetOutDeg(); edge++) {
        const int OutNId = NI.GetOutNId(edge);
        if (NIdSet.IsKey(OutNId)) {
          NewGraph.AddEdge(SrcNId, OutNId); }
      }
    }
  } else {
    for (int n = 0; n < NIdSet.Len(); n++) {
      const int SrcNId = NIdSet[n];
      const TNGraph::TNodeI NI = Graph->GetNI(SrcNId);
      for (int edge = 0; edge < NI.GetOutDeg(); edge++) {
        const int OutNId = NI.GetOutNId(edge);
        if (NIdSet.IsKey(OutNId)) {
          NewGraph.AddEdge(NIdSet.GetKeyId(SrcNId), NIdSet.GetKeyId(OutNId)); }
      }
    }
  }
  return NewGraphPt;
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetSubTreeSz	(	const PGraph &	Graph,
		const int &	StartNId,
		const bool &	FollowOut,
		const bool &	FollowIn,
		int &	TreeSzX,
		int &	TreeDepthX
	)

Returns the BFS tree size (number of nodes) and depth (number of levels) by following in-links (parameter FollowIn = true) and/or out-links (parameter FollowOut = true) of node StartNId.

Definition at line 217 of file bfsdfs.h.

References TBreathFS< PGraph >::DoBfs(), THash< TKey, TDat, THashFunc >::Len(), TMath::Mx(), TInt::Mx, and TBreathFS< PGraph >::NIdDistH.

                                                                                                                                     {
  TBreathFS<PGraph> BFS(Graph);
  BFS.DoBfs(StartNId, FollowOut, FollowIn, -1, TInt::Mx);
  TreeSz = BFS.NIdDistH.Len();
  TreeDepth = 0;
  for (int i = 0; i < BFS.NIdDistH.Len(); i++) {
    TreeDepth = TMath::Mx(TreeDepth, BFS.NIdDistH[i].Val);
  }
  return TreeSz;
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetTreeRootNId

(

const PGraph &

Graph

)

Definition at line 80 of file alg.h.

References Assert, and IsTree().

{ int RootNId; bool Tree; Tree = IsTree(Graph, RootNId);  Assert(Tree);  return RootNId; }

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetTreeSig	(	const PGraph &	Graph,
		const int &	RootNId,
		TIntV &	Sig
	)

Definition at line 484 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), CAssert, TVec< TVal, TSizeTy >::Gen(), gfDirected, HasGraphFlag, IAssert, TVec< TVal, TSizeTy >::Len(), TSnapQueue< TVal >::Push(), and TVec< TVal, TSizeTy >::QSort().

Referenced by TGHash< TDat >::AddKey(), TGHash< TDat >::GetNodeMap(), and TGHash< TDat >::IsGetKeyId().

                                                                     {
  CAssert(HasGraphFlag(typename PGraph::TObj, gfDirected));
  Sig.Gen(Graph->GetNodes(), 0);
  TSnapQueue<int> NIdQ(Graph->GetNodes());
  NIdQ.Push(RootNId);
  int LastPos = 0, NodeCnt = 1;
  while (! NIdQ.Empty()) {
    const typename PGraph::TObj::TNodeI Node = Graph->GetNI(NIdQ.Top());  NIdQ.Pop();
    IAssert(Node.GetInDeg()==0 || Node.GetOutDeg()==0); // child points or is-pointed to by the parent
    if (Node.GetInDeg() != 0) {
      for (int e = 0; e < Node.GetInDeg(); e++) {
        NIdQ.Push(Node.GetInNId(e)); }
    } else if (Node.GetOutDeg() != 0) {
      for (int e = 0; e < Node.GetOutDeg(); e++) {
        NIdQ.Push(Node.GetOutNId(e)); }
    }
    Sig.Add(Node.GetInDeg());
    if (--NodeCnt == 0) {
      for (int i = LastPos; i < Sig.Len(); i++) NodeCnt += Sig[i];
      Sig.QSort(LastPos, Sig.Len()-1, false);
      LastPos = Sig.Len();
    }
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::GetTreeSig	(	const PGraph &	Graph,
		const int &	RootNId,
		TIntV &	Sig,
		TIntPrV &	NodeMap
	)

Definition at line 511 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), CAssert, TVec< TVal, TSizeTy >::Gen(), gfDirected, HasGraphFlag, IAssert, TVec< TVal, TSizeTy >::Len(), TSnapQueue< TVal >::Push(), and TVec< TVal, TSizeTy >::QSort().

                                                                                       {
  CAssert(HasGraphFlag(typename PGraph::TObj, gfDirected));
  NodeMap.Gen(Graph->GetNodes(), 0);
  Sig.Gen(Graph->GetNodes(), 0);
  TSnapQueue<int> NIdQ(Graph->GetNodes());
  NIdQ.Push(RootNId);
  int LastPos = 0, NodeCnt = 1;
  while (! NIdQ.Empty()) {
    const typename PGraph::TObj::TNodeI Node = Graph->GetNI(NIdQ.Top());  NIdQ.Pop();
    IAssert(Node.GetInDeg()==0 || Node.GetOutDeg()==0); // child points or is-pointed to by the parent
    if (Node.GetInDeg() != 0) {
      for (int e = 0; e < Node.GetInDeg(); e++) {
        NIdQ.Push(Node.GetInNId(e)); }
      NodeMap.Add(TIntPr(Node.GetInDeg(), Node.GetId()));
    } else if (Node.GetOutDeg() != 0) {
      for (int e = 0; e < Node.GetOutDeg(); e++) {
        NIdQ.Push(Node.GetOutNId(e)); }
      NodeMap.Add(TIntPr(Node.GetOutDeg(), Node.GetId()));
    }
    if (--NodeCnt == 0) {
      for (int i = LastPos; i < NodeMap.Len(); i++) {
        NodeCnt += NodeMap[i].Val1; }
      NodeMap.QSort(LastPos, NodeMap.Len()-1, false);
      LastPos = NodeMap.Len();
    }
  }
  for (int i = 0; i < NodeMap.Len(); i++) {
    Sig.Add(NodeMap[i].Val1); // degree dignature
    NodeMap[i].Val1 = NodeMap[i].Val2;
    NodeMap[i].Val2 = i;
  }
}

Here is the call graph for this function:

template<class PGraph >

int TSnap::GetTriadEdges	(	const PGraph &	Graph,
		int	SampleEdges = -1
	)

Counts the number of edges that participate in at least one triad.

Considers the graph as undirected.

Parameters

SampleNodes

If !=-1 then compute triads only for a random sample of SampleNodes nodes. Useful for approximate but quick computations.

Definition at line 259 of file triad.h.

References THashSet< TKey, THashFunc >::AddKey(), THashSet< TKey, THashFunc >::Clr(), gfDirected, and THashSet< TKey, THashFunc >::IsKey().

                                                        {
  const bool IsDir = Graph->HasFlag(gfDirected);
  TIntSet NbrH;
  int TriadEdges = 0;
  for(typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    NbrH.Clr(false);
    for (int e = 0; e < NI.GetOutDeg(); e++) {
      if (NI.GetOutNId(e) != NI.GetId()) {
        NbrH.AddKey(NI.GetOutNId(e)); }
    }
    if (IsDir) {
      for (int e = 0; e < NI.GetInDeg(); e++) {
        if (NI.GetInNId(e) != NI.GetId()) {
          NbrH.AddKey(NI.GetInNId(e)); }
      }
    }
    for (int e = 0; e < NI.GetOutDeg(); e++) {
      if (!IsDir && NI.GetId()<NI.GetOutNId(e)) { continue; } // for undirected graphs count each edge only once
      const typename PGraph::TObj::TNodeI SrcNode = Graph->GetNI(NI.GetOutNId(e));
      bool Triad=false;
      for (int e1 = 0; e1 < SrcNode.GetOutDeg(); e1++) {
        if (NbrH.IsKey(SrcNode.GetOutNId(e1))) { Triad=true; break; }
      }
      if (IsDir && ! Triad) {
        for (int e1 = 0; e1 < SrcNode.GetInDeg(); e1++) {
          if (NbrH.IsKey(SrcNode.GetInNId(e1))) { Triad=true; break; }
        }
      }
      if (Triad) { TriadEdges++; }
    }
  }
  return TriadEdges;
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetTriadParticip	(	const PGraph &	Graph,
		TIntPrV &	TriadCntV
	)

Triangle Participation Ratio: For each node counts how many triangles it participates in and then returns a set of pairs (number of triangles, number of such nodes).

Considers the graph as undirected.

Definition at line 372 of file triad.h.

References THash< TKey, TDat, THashFunc >::AddDat(), THash< TKey, TDat, THashFunc >::GetKeyDatPrV(), GetNodeTriads(), and TVec< TVal, TSizeTy >::Sort().

Referenced by TGStat::TakeTriadPart().

                                                               {
  TIntH TriadCntH;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    const int Triads = GetNodeTriads(Graph, NI.GetId());
    TriadCntH.AddDat(Triads) += 1;
  }
  TriadCntH.GetKeyDatPrV(TriadCntV);
  TriadCntV.Sort();
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

int64 TSnap::GetTriads	(	const PGraph &	Graph,
		int	SampleNodes = -1
	)

Returns the number of triangles in a graph.

The function returns the number of unique triples of connected nodes (regardless of the number of edges between each pair of nodes). In other words, the function consideres the Graph as a simple undirected graph.

Parameters

SampleNodes

If !=-1 then compute triads only for a random sample of SampleNodes nodes. Useful for approximate but quick computations.

Definition at line 188 of file triad.h.

References GetTriads().

                                                      {
  int64 OpenTriads, ClosedTriads;
  return GetTriads(Graph, ClosedTriads, OpenTriads, SampleNodes);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetTriads	(	const PGraph &	Graph,
		TIntTrV &	NIdCOTriadV,
		int	SampleNodes = -1
	)

Computes the number of open and close triads for every node of the network.

Considers the graph as undirected.

Parameters

NIdCOTriadV	Triple (node id, open triads: number of pairs of node's neighbors that are not connected, closed triads: number of pairs of node's neighbors that are connected between themselves).
SampleNodes	If !=-1 then compute triads only for a random sample of SampleNodes nodes. Useful for approximate but quick computations.

Definition at line 212 of file triad.h.

References TVec< TVal, TSizeTy >::Add(), THashSet< TKey, THashFunc >::AddKey(), TVec< TVal, TSizeTy >::Clr(), THashSet< TKey, THashFunc >::Clr(), THashSet< TKey, THashFunc >::GetKey(), gfDirected, IAssert, THashSet< TKey, THashFunc >::Len(), TVec< TVal, TSizeTy >::Reserve(), and TVec< TVal, TSizeTy >::Shuffle().

                                                                           {
  const bool IsDir = Graph->HasFlag(gfDirected);
  TIntSet NbrH;
  TIntV NIdV;
  TRnd Rnd(0);

  Graph->GetNIdV(NIdV);
  NIdV.Shuffle(Rnd);
  if (SampleNodes == -1) {
    SampleNodes = Graph->GetNodes(); }
  NIdCOTriadV.Clr(false);
  NIdCOTriadV.Reserve(SampleNodes);
  for (int node = 0; node < SampleNodes; node++) {
    typename PGraph::TObj::TNodeI NI = Graph->GetNI(NIdV[node]);
    if (NI.GetDeg() < 2) {
      NIdCOTriadV.Add(TIntTr(NI.GetId(), 0, 0)); // zero triangles
      continue;
    }
    // find neighborhood
    NbrH.Clr(false);
    for (int e = 0; e < NI.GetOutDeg(); e++) {
      if (NI.GetOutNId(e) != NI.GetId()) {
        NbrH.AddKey(NI.GetOutNId(e)); }
    }
    if (IsDir) {
      for (int e = 0; e < NI.GetInDeg(); e++) {
        if (NI.GetInNId(e) != NI.GetId()) {
          NbrH.AddKey(NI.GetInNId(e)); }
      }
    }
    // count connected neighbors
    int OpenCnt=0, CloseCnt=0;
    for (int srcNbr = 0; srcNbr < NbrH.Len(); srcNbr++) {
      const typename PGraph::TObj::TNodeI SrcNode = Graph->GetNI(NbrH.GetKey(srcNbr));
      for (int dstNbr = srcNbr+1; dstNbr < NbrH.Len(); dstNbr++) {
        const int dstNId = NbrH.GetKey(dstNbr);
        if (SrcNode.IsNbrNId(dstNId)) { CloseCnt++; } // is edge
        else { OpenCnt++; }
      }
    }
    IAssert(2*(OpenCnt+CloseCnt) == NbrH.Len()*(NbrH.Len()-1));
    NIdCOTriadV.Add(TIntTr(NI.GetId(), CloseCnt, OpenCnt));
  }
}

Here is the call graph for this function:

template<class PGraph >

int64 TSnap::GetTriads	(	const PGraph &	Graph,
		int64 &	ClosedTriadsX,
		int64 &	OpenTriadsX,
		int	SampleNodes = -1
	)

Computes the number of Closed and Open triads.

Considers the graph as undirected.

Parameters

SampleNodes

If !=-1 then compute triads only for a random sample of SampleNodes nodes. Useful for approximate but quick computations.

Definition at line 194 of file triad.h.

References TVec< TVal, TSizeTy >::Len().

Referenced by GetClustCf(), GetNodeClustCf(), GetTriads(), PrintInfo(), and TKronMomentsFit::TKronMomentsFit().

                                                                                              {
  TIntTrV NIdCOTriadV;
  GetTriads(Graph, NIdCOTriadV, SampleNodes);
  uint64 closedTriads = 0;
  uint64 openTriads = 0;
  for (int i = 0; i < NIdCOTriadV.Len(); i++) {
    closedTriads += NIdCOTriadV[i].Val2;
    openTriads += NIdCOTriadV[i].Val3;
  }
  //IAssert(closedTriads/3 < (uint64) TInt::Mx);
  //IAssert(openTriads < (uint64) TInt::Mx);
  ClosedTriads = int64(closedTriads/3); // each triad is counted 3 times
  OpenTriads = int64(openTriads);
  return ClosedTriads;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

PGraph TSnap::GetUnDir

(

const PGraph &

Graph

)

Returs an undirected version of the graph. For every edge (u,v) an edge (v,u) is added (if it does not yet exist).

Definition at line 345 of file alg.h.

References MakeUnDir().

                                     {
  PGraph NewGraphPt = PGraph::New();
  *NewGraphPt = *Graph;
  MakeUnDir(NewGraphPt);
  return NewGraphPt;
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::GetWccs	(	const PGraph &	Graph,
		TCnComV &	CnComV
	)

Returns all weakly connected components in a Graph.

Parameters

CnComV

is a vector of connected components. Each component is defined by the IDs of its member nodes.

Definition at line 376 of file cncom.h.

References TVec< TVal, TSizeTy >::Add(), THashSet< TKey, THashFunc >::AddKey(), TVec< TVal, TSizeTy >::Clr(), THashSet< TKey, THashFunc >::Clr(), THashSet< TKey, THashFunc >::Gen(), gfDirected, HasGraphFlag, and TVec< TVal, TSizeTy >::Sort().

Referenced by TSnap::TSnapDetail::_GirvanNewmanGetModularity(), Get1CnCom(), Get1CnComSzCnt(), TCliqueOverlap::GetCPMCommunities(), GetMxWcc(), GetMxWccSz(), and SummarizeConnectedComponents().

                                                   {
  typename PGraph::TObj::TNodeI NI;
  THashSet<TInt> VisitedNId(Graph->GetNodes()+1);
  TSnapQueue<int> NIdQ(Graph->GetNodes()+1);
  TIntV CcNIdV;
  CnComV.Clr();  CcNIdV.Gen(1);
  // zero degree nodes
  for (NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetDeg() == 0) {
      const int NId = NI.GetId();
      VisitedNId.AddKey(NId);
      CcNIdV[0] = NId;  CnComV.Add(CcNIdV);
    }
  }
  // the rest of the nodes
  for (NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    const int NId = NI.GetId();
    if (! VisitedNId.IsKey(NId)) {
      VisitedNId.AddKey(NId);
      NIdQ.Clr(false);  NIdQ.Push(NId);
      CcNIdV.Clr();  CcNIdV.Add(NId);
      while (! NIdQ.Empty()) {
        const typename PGraph::TObj::TNodeI Node = Graph->GetNI(NIdQ.Top());  NIdQ.Pop();
        if (HasGraphFlag(typename PGraph::TObj, gfDirected)) {
          for (int e = 0; e < Node.GetInDeg(); e++) {
            const int InNId = Node.GetInNId(e);
            if (! VisitedNId.IsKey(InNId)) {
              NIdQ.Push(InNId);  VisitedNId.AddKey(InNId);  CcNIdV.Add(InNId); }
          }
        }
        for (int e = 0; e < Node.GetOutDeg(); e++) {
          const int OutNId = Node.GetOutNId(e);
          if (! VisitedNId.IsKey(OutNId)) {
            NIdQ.Push(OutNId);  VisitedNId.AddKey(OutNId);  CcNIdV.Add(OutNId); }
        }
      }
      CcNIdV.Sort(true);
      CnComV.Add(TCnCom(CcNIdV)); // add wcc comoponent
    }
  }
  CnComV.Sort(false);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::GetWccSzCnt	(	const PGraph &	Graph,
		TIntPrV &	WccSzCnt
	)

Returns a distribution of weakly connected component sizes.

Parameters

WccSzCnt

returns a set of pairs (number of nodes in the component, number of such components)

Definition at line 337 of file cncom.h.

References THashSet< TKey, THashFunc >::AddKey(), gfDirected, HasGraphFlag, and TVec< TVal, TSizeTy >::Sort().

Referenced by Get1CnComSzCnt(), PlotWccDistr(), and TGStat::TakeConnComp().

                                                         {
  THashSet<TInt> VisitedNId(Graph->GetNodes());
  TIntH SzToCntH;
  TSnapQueue<int> NIdQ(Graph->GetNodes()+1);
  typename PGraph::TObj::TNodeI NI;
  int Cnt = 0;
  // zero degree nodes
  for (NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetDeg() == 0) { Cnt++;  VisitedNId.AddKey(NI.GetId()); }
  }
  if (Cnt > 0) SzToCntH.AddDat(1, Cnt);
  // the rest of the nodes
  for (NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (! VisitedNId.IsKey(NI.GetId())) {
      VisitedNId.AddKey(NI.GetId());
      NIdQ.Clr(false);  NIdQ.Push(NI.GetId());
      Cnt = 0;
      while (! NIdQ.Empty()) {
        const typename PGraph::TObj::TNodeI Node = Graph->GetNI(NIdQ.Top());  NIdQ.Pop();
        if (HasGraphFlag(typename PGraph::TObj, gfDirected)) {
          for (int e = 0; e < Node.GetInDeg(); e++) {
            const int InNId = Node.GetInNId(e);
            if (! VisitedNId.IsKey(InNId)) { NIdQ.Push(InNId);  VisitedNId.AddKey(InNId); }
          }
        }
        for (int e = 0; e < Node.GetOutDeg(); e++) {
          const int OutNId = Node.GetOutNId(e);
          if (! VisitedNId.IsKey(OutNId)) { NIdQ.Push(OutNId);  VisitedNId.AddKey(OutNId); }
        }
        Cnt++;
      }
      SzToCntH.AddDat(Cnt) += 1;
    }
  }
  SzToCntH.GetKeyDatPrV(WccSzCnt);
  WccSzCnt.Sort(true);
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSnap::GlobalRelabel	(	PNEANet &	Net,
		TPRManager &	PRM,
		const int &	SrcNId,
		const int &	SnkNId
	)

Implements the Global Relabeling heuristic.

Since labels reflect an estimate of the distance from a node to the sink node, every now and then the Global Relabel heuristic will be run. This BFS over the residual network starting from the sink and updates each nodes label as the distance to the sink. Unreacheable nodes from the sink have their labels set to N, where N is the number of nodes.

Definition at line 363 of file flow.cpp.

References TSnap::TPRManager::Capacity(), TQQueue< TVal >::Empty(), TSnap::TPRManager::Excess(), TSnap::TPRManager::Flow(), TNEANet::TNodeI::GetInDeg(), TNEANet::TNodeI::GetInEId(), TNEANet::TNodeI::GetInNId(), TSnap::TPRManager::GetMaxLabel(), TNEANet::TNodeI::GetOutDeg(), TNEANet::TNodeI::GetOutEId(), TNEANet::TNodeI::GetOutNId(), TSnap::TPRManager::IsActive(), TSnap::TPRManager::Label(), TQQueue< TVal >::Pop(), TQQueue< TVal >::Push(), TSnap::TPRManager::PushActive(), TSnap::TPRManager::RemoveActive(), TSnap::TPRManager::SetLabel(), and TQQueue< TVal >::Top().

Referenced by GetMaxFlowIntPR().

                                                                                         {
  TIntQ NodeQ;
  int size = Net->GetMxNId();
  TIntV NodeV(size);
  for (int i = 0; i < size; i++) { NodeV[i] = 0; }
  NodeQ.Push(SnkNId);
  NodeV[SnkNId] = 1;
  int MaxLabel = PRM.GetMaxLabel();
  while (!NodeQ.Empty()) {
    // Backward search
    int NId = NodeQ.Top(); NodeQ.Pop();
    const TNEANet::TNodeI &NI = Net->GetNI(NId);
    // Check all edges that point out of the current node for those over which flow can be returned.
    for (int EdgeN = 0; EdgeN < NI.GetOutDeg(); EdgeN++) {
      int OutNId = NI.GetOutNId(EdgeN);
      int EId = NI.GetOutEId(EdgeN);
      if (!NodeV[OutNId] && PRM.Flow(EId) > 0) {
        NodeV[OutNId] = 1;
        NodeQ.Push(OutNId);
        PRM.SetLabel(OutNId, PRM.Label(NId) + 1);
      }
    }
    // Check all edges that point into the current node for those over which flow can be added.
    for (int EdgeN = 0; EdgeN < NI.GetInDeg(); EdgeN++) {
      int InNId = NI.GetInNId(EdgeN);
      int EId = NI.GetInEId(EdgeN);
      if (!NodeV[InNId] && PRM.Capacity(EId) > PRM.Flow(EId)) {
        NodeV[InNId] = 1;
        NodeQ.Push(InNId);
        PRM.SetLabel(InNId, PRM.Label(NId) + 1);
      }
    }
  }

  for (TNEANet::TNodeI NI = Net->BegNI(); NI != Net->EndNI(); NI++) {
    int NId = NI.GetId();
    if (NodeV[NId]) {
      if (PRM.Excess(NId) > 0 && PRM.Label(NId) < MaxLabel && NId != SnkNId) {
        if (!PRM.IsActive(NId)) { PRM.PushActive(NId); }
      }
    } else {
      if (PRM.IsActive(NId)) { PRM.RemoveActive(NId); }
      PRM.SetLabel(NId, MaxLabel);
    }
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

double TSnap::Infomap	(	PUNGraph &	Graph,
		TCnComV &	CmtyV
	)

Rosvall-Bergstrom community detection algorithm based on information theoretic approach. See: Rosvall M., Bergstrom C. T., Maps of random walks on complex networks reveal community structure, Proc. Natl. Acad. Sci. USA 105, 1118–1123 (2008)

Definition at line 123 of file cmty.cpp.

References TCnCom::Add(), TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), THash< TKey, TDat, THashFunc >::DelKey(), TSnap::TSnapDetail::Equation(), THash< TKey, TDat, THashFunc >::GetDat(), THash< TKey, TDat, THashFunc >::Len(), TSnap::TSnapDetail::MapEquationNew2Modules(), and THash< TKey, TDat, THashFunc >::SortByDat().

                                               {        
  TIntH DegH; 
  TIntFltH PAlpha; // probability of visiting node alpha
  TIntH Module; // module of each node
  TIntFltH Qi; // probability of leaving each module
  float SumPAlphaLogPAlpha = 0.0;
  int Br = 0;
  const int e = Graph->GetEdges(); 

  // initial values
  for (TUNGraph::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    DegH.AddDat(NI.GetId(), NI.GetDeg());
    float d = ((float)NI.GetDeg()/(float)(2*e));
    PAlpha.AddDat(NI.GetId(), d);
    SumPAlphaLogPAlpha += d*log(d);
    Module.AddDat(NI.GetId(),Br);
    Qi.AddDat(Module[Br],1.0);
    Br+=1;
  }

  float MinCodeLength = TSnapDetail::Equation(Graph,PAlpha,SumPAlphaLogPAlpha,Qi);
  float NewCodeLength, PrevIterationCodeLength = 0.0;
  int OldModule, NewModule;

  do {
    PrevIterationCodeLength = MinCodeLength;
      for (TUNGraph::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
        MinCodeLength = TSnapDetail::Equation(Graph, PAlpha, SumPAlphaLogPAlpha, Qi);
        for (int i=0; i<DegH.GetDat(NI.GetId()); i++) {
          OldModule = Module.GetDat(NI.GetId());
          NewModule = Module.GetDat(NI.GetNbrNId(i));
          if (OldModule!=NewModule){
            Module.DelKey(NI.GetId()); 
            Module.AddDat(NI.GetId(),NewModule);
            Qi = TSnapDetail::MapEquationNew2Modules(Graph,Module,Qi,OldModule, NewModule);
            NewCodeLength = TSnapDetail::Equation(Graph,PAlpha,SumPAlphaLogPAlpha, Qi);
            if (NewCodeLength<MinCodeLength) {
              MinCodeLength = NewCodeLength;
              OldModule = NewModule;
            } else {
              Module.DelKey(NI.GetId());
              Module.AddDat(NI.GetId(),OldModule);
            }
          }
       }
     }
   } while (MinCodeLength<PrevIterationCodeLength);

  Module.SortByDat(true);
  int Mod=-1;
  for (int i=0; i<Module.Len(); i++) {
    if (Module[i]>Mod){
      Mod = Module[i];
      TCnCom t;
      for (TUNGraph::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++){
        if (Module.GetDat(NI.GetId())==Mod)
        t.Add(NI.GetId());
      }
      CmtyV.Add(t);
    }
  }

  return MinCodeLength;
}

Here is the call graph for this function:

int TSnap::IntFlowBiDBFS	(	const PNEANet &	Net,
		const int &	CapIndex,
		TIntV &	Flow,
		TIntQ &	FwdNodeQ,
		TIntH &	PredEdgeH,
		TIntQ &	BwdNodeQ,
		TIntH &	SuccEdgeH,
		const int &	SrcNId,
		const int &	SnkNId
	)

Definition at line 4 of file flow.cpp.

References THash< TKey, TDat, THashFunc >::AddDat(), TQQueue< TVal >::Empty(), TNEANet::TNodeI::GetInDeg(), TNEANet::TNodeI::GetInEId(), TNEANet::TNodeI::GetInNId(), TNEANet::TNodeI::GetOutDeg(), TNEANet::TNodeI::GetOutEId(), TNEANet::TNodeI::GetOutNId(), THash< TKey, TDat, THashFunc >::IsKey(), TQQueue< TVal >::Pop(), TQQueue< TVal >::Push(), and TQQueue< TVal >::Top().

Referenced by FindAugV().

                                                                                                                                                                                     {
  FwdNodeQ.Push(SrcNId);
  PredEdgeH.AddDat(SrcNId, -1);
  BwdNodeQ.Push(SnkNId);
  SuccEdgeH.AddDat(SnkNId, -1);
  while (!FwdNodeQ.Empty() && !BwdNodeQ.Empty()) {
    // Forward search
    const TNEANet::TNodeI &FwdNI = Net->GetNI(FwdNodeQ.Top()); FwdNodeQ.Pop();
    // Check all edges that point into the current node for those over which flow can be returned.
    for (int EdgeN = 0; EdgeN < FwdNI.GetInDeg(); EdgeN++) {
      int NextNId = FwdNI.GetInNId(EdgeN);
      int NextEId = FwdNI.GetInEId(EdgeN);
      if (!PredEdgeH.IsKey(NextNId) && Flow[NextEId] > 0) {
        PredEdgeH.AddDat(NextNId, NextEId);
        if (SuccEdgeH.IsKey(NextNId)) {
          return NextNId;
        }
        FwdNodeQ.Push(NextNId);
      }
    }
    // Check all edges that point out of the current node for those over which flow can be added.
    for (int EdgeN = 0; EdgeN < FwdNI.GetOutDeg(); EdgeN++) {
      int NextNId = FwdNI.GetOutNId(EdgeN);
      int NextEId = FwdNI.GetOutEId(EdgeN);
      if (!PredEdgeH.IsKey(NextNId) && Net->GetIntAttrIndDatE(NextEId, CapIndex) > Flow[NextEId]) {
        PredEdgeH.AddDat(NextNId, NextEId);
        if (SuccEdgeH.IsKey(NextNId)) {
          return NextNId;
        }
        FwdNodeQ.Push(NextNId);
      }
    }
    // Backward search
    const TNEANet::TNodeI &BwdNI = Net->GetNI(BwdNodeQ.Top());  BwdNodeQ.Pop();
    // Check all edges that point out of the current node for those over which flow can be returned.
    for (int EdgeN = 0; EdgeN < BwdNI.GetOutDeg(); EdgeN++) {
      int PrevNId = BwdNI.GetOutNId(EdgeN);
      int PrevEId = BwdNI.GetOutEId(EdgeN);
      if (!SuccEdgeH.IsKey(PrevNId) && Flow[PrevEId] > 0) {
        SuccEdgeH.AddDat(PrevNId, PrevEId);
        if (PredEdgeH.IsKey(PrevNId)) {
          return PrevNId;
        }
        BwdNodeQ.Push(PrevNId);
      }
    }
    // Check all edges that point into the current node for those over which flow can be added.
    for (int EdgeN = 0; EdgeN < BwdNI.GetInDeg(); EdgeN++) {
      int PrevNId = BwdNI.GetInNId(EdgeN);
      int PrevEId = BwdNI.GetInEId(EdgeN);
      if (!SuccEdgeH.IsKey(PrevNId) && Net->GetIntAttrIndDatE(PrevEId, CapIndex) > Flow[PrevEId]) {
        SuccEdgeH.AddDat(PrevNId, PrevEId);
        if (PredEdgeH.IsKey(PrevNId)) {
          return PrevNId;
        }
        BwdNodeQ.Push(PrevNId);
      }
    }
  }
  return -1;
}

Here is the call graph for this function:

Here is the caller graph for this function:

bool TSnap::IsAllValVNeg	(	TFltV &	ValV,
		const bool &	InvertSign
	)

Definition at line 163 of file gsvd.cpp.

References TVec< TVal, TSizeTy >::Len().

Referenced by GetEigVec(), and GetSngVec().

                                                       {
  bool IsAllNeg=true;
  for (int i = 0; i < ValV.Len(); i++) {
    if (ValV[i]>0.0) { IsAllNeg=false; break; }
  }
  if (IsAllNeg && InvertSign) {
    for (int i = 0; i < ValV.Len(); i++) { 
      ValV[i] = -ValV[i]; }
  }
  return IsAllNeg;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

bool TSnap::IsConnected

(

const PGraph &

Graph

)

Tests whether the Graph is (weakly) connected.

Definition at line 305 of file cncom.h.

References IsWeaklyConn().

Referenced by IsTree().

                                      {
  return IsWeaklyConn(Graph);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

bool TSnap::IsTree	(	const PGraph &	Graph,
		int &	RootNIdX
	)

Definition at line 460 of file alg.h.

References IsConnected().

Referenced by TGHash< TDat >::AddKey(), TGHash< TDat >::GetNodeMap(), GetTreeRootNId(), and TGHash< TDat >::IsGetKeyId().

                                               {
  if (Graph->GetNodes() == 1 && Graph->GetEdges() == 0) {
    RootNId = Graph->BegNI().GetId();
    return true;
  }
  RootNId = -1;
  if (Graph->GetNodes() != Graph->GetEdges()+1) { return false; }
  int NZeroOutDeg = 0;
  int ZeroOutDegN = -1;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetOutDeg() == 0) {
      ZeroOutDegN = NI.GetId();  NZeroOutDeg++;
    }
    if (NI.GetDeg() == 0) { return false; } // isolated nodes
  }
  if (NZeroOutDeg==1) {
    if (! TSnap::IsConnected(Graph)) { return false; }
    RootNId = ZeroOutDegN;  return true;
  }
  return false;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

bool TSnap::IsWeaklyConn

(

const PGraph &

Graph

)

Tests whether the Graph is weakly connected.

Definition at line 310 of file cncom.h.

References gfDirected, HasGraphFlag, and TSnapQueue< TVal >::Push().

Referenced by IsConnected().

                                       {
  if (Graph->Empty()) {
    return true;
  }
  THashSet<TInt> VisitedNId(Graph->GetNodes());
  TSnapQueue<int> NIdQ(Graph->GetNodes()+1);
  typename PGraph::TObj::TNodeI NI;
  // the rest of the nodes
  NIdQ.Push(Graph->BegNI().GetId());
  while (! NIdQ.Empty()) {
    const typename PGraph::TObj::TNodeI Node = Graph->GetNI(NIdQ.Top());  NIdQ.Pop();
    if (HasGraphFlag(typename PGraph::TObj, gfDirected)) {
      for (int e = 0; e < Node.GetInDeg(); e++) {
        const int InNId = Node.GetInNId(e);
        if (! VisitedNId.IsKey(InNId)) { NIdQ.Push(InNId);  VisitedNId.AddKey(InNId); }
      }
    }
    for (int e = 0; e < Node.GetOutDeg(); e++) {
      const int OutNId = Node.GetOutNId(e);
      if (! VisitedNId.IsKey(OutNId)) { NIdQ.Push(OutNId);  VisitedNId.AddKey(OutNId); }
    }
  }
  if (VisitedNId.Len() < Graph->GetNodes()) { return false; }
  return true;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

PGraph TSnap::LoadConnList

(

const TStr &

InFNm

)

Loads a (directed, undirected or multi) graph from a text file InFNm with 1 node and all its edges in a single line.

Loads Whitespace separated file of several columns: <source node="" id>=""> <destination node="" id1>=""> <destination node="" id2>="">

Whitespace separated file of several columns: <source node="" id>=""> <destination node="" id1>=""> <destination node="" id2>=""> ... First column of each line contains a source node id followed by ids of the destination nodes. For example, '1 2 3' encodes edges 1–>2 and 1–>3. Note that this format allows for saving isolated nodes.

Definition at line 152 of file gio.h.

References TSsParser::GetInt(), TSsParser::IsInt(), TSsParser::Len(), TSsParser::Next(), and ssfWhiteSep.

                                       {
  TSsParser Ss(InFNm, ssfWhiteSep, true, true, true);
  PGraph Graph = PGraph::TObj::New();
  while (Ss.Next()) {
    if (! Ss.IsInt(0)) { continue; }
    const int SrcNId = Ss.GetInt(0);
    if (! Graph->IsNode(SrcNId)) { Graph->AddNode(SrcNId); }
    for (int dst = 1; dst < Ss.Len(); dst++) {
      const int DstNId = Ss.GetInt(dst);
      if (! Graph->IsNode(DstNId)) { Graph->AddNode(DstNId); }
      Graph->AddEdge(SrcNId, DstNId);
    }
  }
  Graph->Defrag();
  return Graph;
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::LoadConnListStr	(	const TStr &	InFNm,
		TStrHash< TInt > &	StrToNIdH
	)

Loads a (directed, undirected or multi) graph from a text file InFNm with 1 node and all its edges in a single line.

Loads Whitespace separated file of several columns: <source node="" id>=""> <destination node="" id1>=""> <destination node="" id2>="">, with a mapping of strings to node IDs.

Whitespace separated file of several columns: <source node="" name>=""> <destination node name 1> <destination node name 2> ... First colum of each line contains a source node name followed by ids of the destination nodes. For example, 'A B C' encodes edges A–>B and A–>C. Note that this format allows for saving isolated nodes. stores the mapping from node names to node ids.

Definition at line 176 of file gio.h.

References TStrHash< TDat, TStringPool, THashFunc >::AddDatId(), TSsParser::Len(), TSsParser::Next(), and ssfWhiteSep.

                                                                     {
  TSsParser Ss(InFNm, ssfWhiteSep, true, true, true);
  PGraph Graph = PGraph::TObj::New();
  while (Ss.Next()) {
    const int SrcNId = StrToNIdH.AddDatId(Ss[0]);
    if (! Graph->IsNode(SrcNId)) { Graph->AddNode(SrcNId); }
    for (int dst = 1; dst < Ss.Len(); dst++) {
      const int DstNId = StrToNIdH.AddDatId(Ss[dst]);
      if (! Graph->IsNode(DstNId)) { Graph->AddNode(DstNId); }
      Graph->AddEdge(SrcNId, DstNId);
    }
  }
  Graph->Defrag();
  return Graph;
}

Here is the call graph for this function:

PNGraph TSnap::LoadDyNet

(

const TStr &

FNm

)

For more info see ORA Network Analysis Data (http://www.casos.cs.cmu.edu/computational_tools/data2.php)

Loads a directed network in the DyNetML format. Loads only the first network in the file FNm.

Definition at line 4 of file gio.cpp.

References TNGraph::AddEdge(), THashSet< TKey, THashFunc >::AddKey(), TNGraph::AddNode(), TXmlLx::GetArg(), THashSet< TKey, THashFunc >::GetKeyId(), TXmlLx::GetSym(), IAssert, TNGraph::IsNode(), TZipIn::IsZipFNm(), TZipIn::New(), TFIn::New(), TNGraph::New(), TXmlLx::Sym, TXmlLx::TagNm, xspTruncate, xsyEof, and xsySTag.

                                   {
  TXmlLx XmlLx(TZipIn::IsZipFNm(FNm)?TZipIn::New(FNm):TFIn::New(FNm), xspTruncate);
  THashSet<TStr> NIdStr;
  while (XmlLx.GetSym()!=xsyEof) {
    if (XmlLx.Sym==xsySTag && XmlLx.TagNm=="network") {
      PNGraph G = TNGraph::New();
      XmlLx.GetSym();
      while (XmlLx.TagNm=="link") {
        TStr Str1, Val1, Str2, Val2;
        XmlLx.GetArg(0, Str1, Val1);  XmlLx.GetArg(1, Str2, Val2);
        IAssert(Str1=="source" && Str2=="target");
        NIdStr.AddKey(Val1); NIdStr.AddKey(Val2);
        const int src=NIdStr.GetKeyId(Val1);
        const int dst=NIdStr.GetKeyId(Val2);
        if (! G->IsNode(src)) { G->AddNode(src); }
        if (! G->IsNode(dst)) { G->AddNode(dst); }
        G->AddEdge(src, dst);
        XmlLx.GetSym();
      }
      return G;
    }
  }
  return PNGraph();
}

Here is the call graph for this function:

TVec< PNGraph > TSnap::LoadDyNetGraphV

(

const TStr &

FNm

)

For more info see ORA Network Analysis Data (http://www.casos.cs.cmu.edu/computational_tools/data2.php)

Loads directed networks in the DyNetML format. Loads all the networks in the file FNm.

Definition at line 30 of file gio.cpp.

References TVec< TVal, TSizeTy >::Add(), TNGraph::AddEdge(), THashSet< TKey, THashFunc >::AddKey(), TNGraph::AddNode(), TXmlLx::GetArg(), THashSet< TKey, THashFunc >::GetKeyId(), TXmlLx::GetSym(), IAssert, TNGraph::IsNode(), TZipIn::IsZipFNm(), TZipIn::New(), TFIn::New(), TNGraph::New(), TXmlLx::Sym, TXmlLx::TagNm, xspTruncate, xsyEof, and xsySTag.

                                               {
  TXmlLx XmlLx(TZipIn::IsZipFNm(FNm)?TZipIn::New(FNm):TFIn::New(FNm), xspTruncate);
  TVec<PNGraph> GraphV;
  THashSet<TStr> NIdStr;
  while (XmlLx.GetSym()!=xsyEof) {
    if (XmlLx.Sym==xsySTag && XmlLx.TagNm=="network") {
      PNGraph G = TNGraph::New();
      GraphV.Add(G);
      XmlLx.GetSym();
      while (XmlLx.TagNm=="link") {
        TStr Str1, Val1, Str2, Val2;
        XmlLx.GetArg(0, Str1, Val1);  XmlLx.GetArg(1, Str2, Val2);
        IAssert(Str1=="source" && Str2=="target");
        NIdStr.AddKey(Val1); NIdStr.AddKey(Val2);
        const int src=NIdStr.GetKeyId(Val1);
        const int dst=NIdStr.GetKeyId(Val2);
        if (! G->IsNode(src)) { G->AddNode(src); }
        if (! G->IsNode(dst)) { G->AddNode(dst); }
        G->AddEdge(src, dst);
        XmlLx.GetSym();
      }
    }
  }
  return GraphV;
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::LoadEdgeList	(	const TStr &	InFNm,
		const int &	SrcColId,
		const int &	DstColId
	)

Loads a (directed, undirected or multi) graph from a text file InFNm with 1 edge per line (whitespace separated columns, integer node ids).

Loads the format saved by TSnap::SaveEdgeList()

Whitespace separated file of several columns: ... <source node="" id>=""> ... <destination node="" id>=""> ... SrcColId and DstColId are column indexes of source/destination (integer!) node ids. This means there is one edge per line and node IDs are assumed to be integers.

Definition at line 68 of file gio.h.

References TSsParser::GetInt(), TSsParser::Next(), and ssfWhiteSep.

                                                                                 {
  TSsParser Ss(InFNm, ssfWhiteSep, true, true, true);
  PGraph Graph = PGraph::TObj::New();
  int SrcNId, DstNId;
  while (Ss.Next()) {
    if (! Ss.GetInt(SrcColId, SrcNId) || ! Ss.GetInt(DstColId, DstNId)) { continue; }
    if (! Graph->IsNode(SrcNId)) { Graph->AddNode(SrcNId); }
    if (! Graph->IsNode(DstNId)) { Graph->AddNode(DstNId); }
    Graph->AddEdge(SrcNId, DstNId);
  }
  Graph->Defrag();
  return Graph;
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::LoadEdgeList	(	const TStr &	InFNm,
		const int &	SrcColId,
		const int &	DstColId,
		const char &	Separator
	)

Loads a (directed, undirected or multi) graph from a text file InFNm with 1 edge per line ('Separator' separated columns, integer node ids).

Loads the format saved by TSnap::SaveEdgeList() if we set Separator=''.

'Separator' separated file of several columns: ... <source node="" id>=""> ... <destination node="" id>=""> ... SrcColId and DstColId are column indexes of source/destination (integer!) node ids. This means there is one edge per line and node IDs are assumed to be integers.

Definition at line 88 of file gio.h.

References TSsParser::GetInt(), and TSsParser::Next().

                                                                                                        {
  TSsParser Ss(InFNm, Separator);
  PGraph Graph = PGraph::TObj::New();
  int SrcNId, DstNId;
  while (Ss.Next()) {
    if (! Ss.GetInt(SrcColId, SrcNId) || ! Ss.GetInt(DstColId, DstNId)) { continue; }
    if (! Graph->IsNode(SrcNId)) { Graph->AddNode(SrcNId); }
    if (! Graph->IsNode(DstNId)) { Graph->AddNode(DstNId); }
    Graph->AddEdge(SrcNId, DstNId);
  }
  Graph->Defrag();
  return Graph;
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::LoadEdgeListStr	(	const TStr &	InFNm,
		const int &	SrcColId,
		const int &	DstColId
	)

Loads a (directed, undirected or multi) graph from a text file InFNm with 1 edge per line (whitespace separated columns, arbitrary string node ids).

Loads the format saved by TSnap::SaveEdgeList(), where node IDs are strings.

Whitespace separated file of several columns: ... <source node="" id>=""> ... <destination node="" id>=""> ... SrcColId and DstColId are column indexes of source/destination (string) node ids. This means there is one edge per line and node IDs can be arbitrary STRINGs. Note that the mapping of node names to ids is discarded.

Definition at line 109 of file gio.h.

References TStrHash< TDat, TStringPool, THashFunc >::AddKey(), Mega, TSsParser::Next(), and ssfWhiteSep.

                                                                                    {
  TSsParser Ss(InFNm, ssfWhiteSep);
  PGraph Graph = PGraph::TObj::New();
  TStrHash<TInt> StrToNIdH(Mega(1), true); // hash-table mapping strings to integer node ids
  while (Ss.Next()) {
    const int SrcNId = StrToNIdH.AddKey(Ss[SrcColId]);
    const int DstNId = StrToNIdH.AddKey(Ss[DstColId]);
    if (! Graph->IsNode(SrcNId)) { Graph->AddNode(SrcNId); }
    if (! Graph->IsNode(DstNId)) { Graph->AddNode(DstNId); }
    Graph->AddEdge(SrcNId, DstNId);
  }
  Graph->Defrag();
  return Graph;
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::LoadEdgeListStr	(	const TStr &	InFNm,
		const int &	SrcColId,
		const int &	DstColId,
		TStrHash< TInt > &	StrToNIdH
	)

Loads a (directed, undirected or multi) graph from a text file InFNm with 1 edge per line (whitespace separated columns, arbitrary string node ids).

Loads the format saved by TSnap::SaveEdgeList(), where node IDs are strings and mapping of strings to node ids are stored.

Whitespace separated file of several columns: ... <source node="" id>=""> ... <destination node="" id>=""> ... SrcColId and DstColId are column indexes of source/destination (string) node ids. This means there is one edge per line and node IDs can be arbitrary STRINGs. The mapping of strings to node ids in stored in StrToNIdH. To map between node names and ids use: NId = StrToNIdH.GetKeyId(NodeName) and TStr NodeName = StrToNIdH.GetKey(NId);

Definition at line 132 of file gio.h.

References TStrHash< TDat, TStringPool, THashFunc >::AddKey(), TSsParser::Next(), and ssfWhiteSep.

                                                                                                               {
  TSsParser Ss(InFNm, ssfWhiteSep);
  PGraph Graph = PGraph::TObj::New();
  while (Ss.Next()) {
    const int SrcNId = StrToNIdH.AddKey(Ss[SrcColId]);
    const int DstNId = StrToNIdH.AddKey(Ss[DstColId]);
    if (! Graph->IsNode(SrcNId)) { Graph->AddNode(SrcNId); }
    if (! Graph->IsNode(DstNId)) { Graph->AddNode(DstNId); }
    Graph->AddEdge(SrcNId, DstNId);
  }
  Graph->Defrag();
  return Graph;
}

Here is the call graph for this function:

template<class PGraph >

PGraph TSnap::LoadPajek

(

const TStr &

InFNm

)

Loads a (directed, undirected or multi) graph from Pajek .PAJ format file.

Function supports both the 1 edge per line (<source> <destination> <weight>) as well as the 1 node per line (<source> <destination1> <destination2> ...) formats.

Definition at line 193 of file gio.h.

References EAssert, TSsParser::Eof(), TSsParser::GetInt(), TSsParser::IsInt(), TSsParser::Len(), TSsParser::Next(), ssfSpaceSep, and TSsParser::ToLc().

                                    {
  PGraph Graph = PGraph::TObj::New();
  TSsParser Ss(InFNm, ssfSpaceSep, true, true, true);
  while ((Ss.Len()==0 || strstr(Ss[0], "*vertices") == NULL) && ! Ss.Eof()) {
    Ss.Next();  Ss.ToLc(); }
  // nodes
  bool EdgeList = true;
  EAssert(strstr(Ss[0], "*vertices") != NULL);
  while (Ss.Next()) {
    Ss.ToLc();
    if (Ss.Len()>0 && Ss[0][0] == '%') { continue; } // comment
    if (strstr(Ss[0], "*arcslist")!=NULL || strstr(Ss[0],"*edgeslist")!=NULL) { EdgeList=false; break; } 
    if (strstr(Ss[0], "*arcs")!=NULL || strstr(Ss[0],"*edges")!=NULL) { break; } // arcs are directed, edges are undirected
    Graph->AddNode(Ss.GetInt(0));
  }
  // edges
  while (Ss.Next()) {
    if (Ss.Len()>0 && Ss[0][0] == '%') { continue; } // comment
    if (Ss.Len()>0 && Ss[0][0] == '*') { break; }
    if (EdgeList) {
      // <source> <destination> <weight>
      if (Ss.Len() >= 3 && Ss.IsInt(0) && Ss.IsInt(1)) {
        Graph->AddEdge(Ss.GetInt(0), Ss.GetInt(1)); }
    } else {
      // <source> <destination1> <destination2> <destination3> ...
      const int SrcNId = Ss.GetInt(0);
      for (int i = 1; i < Ss.Len(); i++) {
        Graph->AddEdge(SrcNId, Ss.GetInt(i)); }
    }
  }
  return Graph;
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::MakeUnDir

(

const PGraph &

Graph

)

Makes the graph undirected. For every edge (u,v) an edge (v,u) is added (if it does not yet exist).

Definition at line 353 of file alg.h.

References TVec< TVal, TSizeTy >::Add(), CAssert, gfDirected, HasGraphFlag, and TVec< TVal, TSizeTy >::Len().

Referenced by GetUnDir().

                                    {
  CAssert(HasGraphFlag(typename PGraph::TObj, gfDirected)); // graph has to be directed
  TIntPrV EdgeV;
  for (typename PGraph::TObj::TEdgeI EI = Graph->BegEI(); EI < Graph->EndEI(); EI++) {
    const int SrcNId = EI.GetSrcNId();
    const int DstNId = EI.GetDstNId();
    if (! Graph->IsEdge(DstNId, SrcNId)) {
      EdgeV.Add(TIntPr(DstNId, SrcNId));
    }
  }
  for (int i = 0; i < EdgeV.Len(); i++) {
    Graph->AddEdge(EdgeV[i].Val1, EdgeV[i].Val2);
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::PlotClustCf	(	const PGraph &	Graph,
		const TStr &	FNmPref,
		TStr	DescStr = TStr()
	)

Plots the distribution of clustering coefficient of a Graph.

Definition at line 111 of file statplot.h.

References TGnuPlot::AddPlot(), TStr::CStr(), TStr::Empty(), TStr::Fmt(), GetClustCf(), gpsLog10XY, gpwLinesPoints, TGnuPlot::SavePng(), TGnuPlot::SetScale(), and TGnuPlot::SetXYLabel().

                                                                         {
  TFltPrV DegToCCfV;
  int64 ClosedTriads, OpenTriads;
  const double CCF = GetClustCf(Graph, DegToCCfV, ClosedTriads, OpenTriads);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot GnuPlot("ccf."+FNmPref,
    TStr::Fmt("%s. G(%d, %d). Average clustering: %.4f  OpenTriads: %d (%.4f)  ClosedTriads: %d (%.4f)", DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges(),
    CCF, OpenTriads, OpenTriads/double(OpenTriads+ClosedTriads), ClosedTriads, ClosedTriads/double(OpenTriads+ClosedTriads)));
  GnuPlot.AddPlot(DegToCCfV, gpwLinesPoints, "", "pt 6");
  GnuPlot.SetXYLabel("Node degree", "Average clustering coefficient");
  GnuPlot.SetScale(gpsLog10XY);
  GnuPlot.SavePng();
}

Here is the call graph for this function:

void TSnap::PlotEigValDistr	(	const PUNGraph &	Graph,
		const int &	EigVals,
		const TStr &	FNmPref,
		TStr	DescStr
	)

Plots the distribution of components of the leading eigen-vector of the Graph adjacency matrix. Plots first EigVals values.

Definition at line 14 of file statplot.cpp.

References THash< TKey, TDat, THashFunc >::AddDat(), TStr::CStr(), TStr::Empty(), TVec< TVal, TSizeTy >::Empty(), TStr::Fmt(), GetEigVals(), THash< TKey, TDat, THashFunc >::GetKeyDatPrV(), gpsAuto, gpwLinesPoints, TVec< TVal, TSizeTy >::Last(), TVec< TVal, TSizeTy >::Len(), TGnuPlot::PlotValV(), and TVec< TVal, TSizeTy >::Sort().

                                                                                                   {
  const int NBuckets = 50;
  TFltV EigValV;
  for (int f = 1; EigValV.Empty() && f < 4; f++) {
    TSnap::GetEigVals(Graph, f*EigVals, EigValV);
  }
  EigValV.Sort(true);
  THash<TFlt, TFlt> BucketCntH;
  double Step = (EigValV.Last()-EigValV[0]) / double(NBuckets-1);
  for (int i = 0; i < NBuckets; i++) {
    BucketCntH.AddDat(EigValV[0]+Step*(i+0.5), 0);
  }
  for (int i = 0; i < EigValV.Len(); i++) {
    const int Bucket = (int) floor((EigValV[i]-EigValV[0]) / Step);
    BucketCntH[Bucket] += 1;
  }
  TFltPrV EigCntV;
  BucketCntH.GetKeyDatPrV(EigCntV);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot::PlotValV(EigCntV, "eigDistr."+FNmPref, TStr::Fmt("%s. G(%d, %d). Largest eig val = %f", DescStr.CStr(),
    Graph->GetNodes(), Graph->GetEdges(), EigValV.Last().Val), "Eigen value", "Count", gpsAuto, false, gpwLinesPoints);
}

Here is the call graph for this function:

void TSnap::PlotEigValRank	(	const PUNGraph &	Graph,
		const int &	EigVals,
		const TStr &	FNmPref,
		TStr	DescStr
	)

Plots the eigen-value rank distribution of the Graph adjacency matrix. Plots first EigVals eigenvalues.

Definition at line 5 of file statplot.cpp.

References TStr::CStr(), TStr::Empty(), TStr::Fmt(), GetEigVals(), gpsLog10XY, gpwLinesPoints, TGnuPlot::PlotValV(), and TVec< TVal, TSizeTy >::Sort().

                                                                                                  {
  TFltV EigValV;
  TSnap::GetEigVals(Graph, EigVals, EigValV);
  EigValV.Sort(false);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot::PlotValV(EigValV, "eigVal."+FNmPref, TStr::Fmt("%s. G(%d, %d). Largest eig val = %f",
    DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges(), EigValV[0].Val), "Rank", "Eigen value", gpsLog10XY, false, gpwLinesPoints);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::PlotHops	(	const PGraph &	Graph,
		const TStr &	FNmPref,
		TStr	DescStr = TStr(),
		const bool &	IsDir = false,
		const int &	NApprox = 32
	)

Plots the cumulative distribution of the shortest path lengths of a Graph. Implementation is based on ANF.

Parameters

IsDir

false: ignore edge directions and consider graph as undirected.

Definition at line 126 of file statplot.h.

References TGnuPlot::AddPlot(), TSnap::TSnapDetail::CalcEffDiam(), TStr::CStr(), TStr::Empty(), TStr::Fmt(), GetAnf(), gpsLog10Y, gpwLinesPoints, TGnuPlot::SavePng(), TGnuPlot::SetScale(), and TGnuPlot::SetXYLabel().

                                                                                                             {
  TIntFltKdV DistNbrsV;
  TSnap::GetAnf(Graph, DistNbrsV, -1, IsDir, NApprox);
  const double EffDiam = TSnap::TSnapDetail::CalcEffDiam(DistNbrsV, 0.9);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot GnuPlot("hop."+FNmPref, TStr::Fmt("%s. Hop plot. EffDiam: %g, G(%d, %d)",
    DescStr.CStr(), EffDiam, Graph->GetNodes(), Graph->GetEdges()));
  GnuPlot.SetXYLabel("Number of hops", "Number of pairs of nodes");
  GnuPlot.SetScale(gpsLog10Y);
  GnuPlot.AddPlot(DistNbrsV, gpwLinesPoints, "", "pt 6");
  GnuPlot.SavePng();
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::PlotInDegDistr	(	const PGraph &	Graph,
		const TStr &	FNmPref,
		TStr	DescStr = TStr(),
		const bool &	PlotCCdf = false,
		const bool &	PowerFit = false
	)

Plots the in-degree distribution of a Graph.

Parameters

PlotCCdf	Plots the distribution as a Complementary Cummulative distribution function.
PowerFit	Fits a Power-Law to the distribution.

Definition at line 47 of file statplot.h.

References TStr::CStr(), TStr::Empty(), TStr::Fmt(), TGUtil::GetCCdf(), GetInDegCnt(), gpsLog10XY, gpwLinesPoints, TVec< TVal, TSizeTy >::Len(), and TGnuPlot::PlotValV().

                                                                                                                        {
  TIntPrV DegCntV;
  TSnap::GetInDegCnt(Graph, DegCntV);
  const double AvgDeg = 2*Graph->GetEdges()/double(Graph->GetNodes());
  int AboveAvg=0, Above2Avg=0;
  for (int i = 0; i < DegCntV.Len(); i++) {
    if (DegCntV[i].Val1 > AvgDeg) { AboveAvg += DegCntV[i].Val2; }
    if (DegCntV[i].Val1 > 2*AvgDeg) { Above2Avg += DegCntV[i].Val2; }
  }
  if (PlotCCdf) {
    DegCntV = TGUtil::GetCCdf(DegCntV); }
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot::PlotValV(DegCntV, (PlotCCdf?"inDegC.":"inDeg.")+FNmPref,
    TStr::Fmt("%s. G(%d, %d). %d (%.4f) nodes with in-deg > avg deg (%.1f), %d (%.4f) with >2*avg.deg", DescStr.CStr(),
      Graph->GetNodes(), Graph->GetEdges(), AboveAvg, AboveAvg/double(Graph->GetNodes()), AvgDeg, Above2Avg, Above2Avg/double(Graph->GetNodes())),
    "In-degree", PlotCCdf?"Count (CCDF)":"Count", gpsLog10XY, PowerFit, gpwLinesPoints);
}

Here is the call graph for this function:

void TSnap::PlotInvParticipRat	(	const PUNGraph &	Graph,
		const int &	MaxEigVecs,
		const int &	TimeLimit,
		const TStr &	FNmPref,
		TStr	DescStr = TStr()
	)

Plots the inverse participation ratio. See Spectra of "real-world" graphs: Beyond the semicircle law by Farkas, Derenyi, Barabasi and Vicsek.

Definition at line 39 of file statplot.cpp.

References TVec< TVal, TSizeTy >::Add(), TStr::CStr(), TStr::Empty(), TVec< TVal, TSizeTy >::Empty(), TStr::Fmt(), GetInvParticipRat(), gpsLog10Y, gpwPoints, TVec< TVal, TSizeTy >::Last(), TVec< TVal, TSizeTy >::Len(), and TGnuPlot::PlotValV().

                                                                                                                               {
  TFltPrV EigIprV;
  GetInvParticipRat(Graph, MaxEigVecs, TimeLimit, EigIprV);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  if (EigIprV.Empty()) { DescStr+=". FAIL"; EigIprV.Add(TFltPr(-1,-1)); return; }
  TGnuPlot::PlotValV(EigIprV, "eigIPR."+FNmPref, TStr::Fmt("%s. G(%d, %d). Largest eig val = %f (%d values)",
    DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges(), EigIprV.Last().Val1(), EigIprV.Len()),
    "Eigenvalue", "Inverse Participation Ratio of corresponding Eigenvector", gpsLog10Y, false, gpwPoints);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::PlotKCoreEdges	(	const PGraph &	Graph,
		const TStr &	FNmPref,
		TStr	DescStr = TStr()
	)

Plots the k-Core edge-size distribution: Core k vs. number of edges in k-core.

Definition at line 175 of file statplot.h.

References TStr::CStr(), TStr::Empty(), TStr::Fmt(), GetKCoreEdges(), gpsLog10Y, gpwLinesPoints, and TGnuPlot::PlotValV().

                                                                            {
  TIntPrV CoreEdgesV;
  TSnap::GetKCoreEdges(Graph, CoreEdgesV);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot::PlotValV(CoreEdgesV, "coreEdges."+FNmPref, TStr::Fmt("%s. G(%d, %d).", DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges()), "k-Core", "Number of edges in the k-Core", gpsLog10Y, false, gpwLinesPoints);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::PlotKCoreNodes	(	const PGraph &	Graph,
		const TStr &	FNmPref,
		TStr	DescStr = TStr()
	)

Plots the k-Core node-size distribution: Core k vs. number of nodes in k-core.

Definition at line 167 of file statplot.h.

References TStr::CStr(), TStr::Empty(), TStr::Fmt(), GetKCoreNodes(), gpsLog10Y, gpwLinesPoints, and TGnuPlot::PlotValV().

                                                                            {
  TIntPrV CoreNodesV;
  TSnap::GetKCoreNodes(Graph, CoreNodesV);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot::PlotValV(CoreNodesV, "coreNodes."+FNmPref, TStr::Fmt("%s. G(%d, %d).", DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges()), "k-Core", "Number of nodes in the k-Core", gpsLog10Y, false, gpwLinesPoints);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::PlotOutDegDistr	(	const PGraph &	Graph,
		const TStr &	FNmPref,
		TStr	DescStr = TStr(),
		const bool &	PlotCCdf = false,
		const bool &	PowerFit = false
	)

Plots the out-degree distribution of a Graph.

Parameters

PlotCCdf	Plots the distribution as a Complementary Cumulative Distribution Function (CCDF).
PowerFit	Fits a Power-Law to the distribution.

Definition at line 66 of file statplot.h.

References TStr::CStr(), TStr::Empty(), TStr::Fmt(), TGUtil::GetCCdf(), GetOutDegCnt(), gpsLog10XY, gpwLinesPoints, TVec< TVal, TSizeTy >::Len(), and TGnuPlot::PlotValV().

                                                                                                                         {
  TIntPrV DegCntV;
  TSnap::GetOutDegCnt(Graph, DegCntV);
  const double AvgDeg = 2*Graph->GetEdges()/double(Graph->GetNodes());
  int AboveAvg=0, Above2Avg=0;
  for (int i = 0; i < DegCntV.Len(); i++) {
    if (DegCntV[i].Val1 > AvgDeg) { AboveAvg += DegCntV[i].Val2; }
    if (DegCntV[i].Val1 > 2*AvgDeg) { Above2Avg += DegCntV[i].Val2; }
  }
  if (PlotCCdf) {
    DegCntV = TGUtil::GetCCdf(DegCntV); }
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot::PlotValV(DegCntV, (PlotCCdf?"outDegC.":"outDeg.")+FNmPref,
    TStr::Fmt("%s. G(%d, %d). %d (%.4f) nodes with out-deg > avg deg (%.1f), %d (%.4f) with >2*avg.deg", DescStr.CStr(),
      Graph->GetNodes(), Graph->GetEdges(), AboveAvg, AboveAvg/double(Graph->GetNodes()), AvgDeg, Above2Avg, Above2Avg/double(Graph->GetNodes())),
    "Out-degree", PlotCCdf?"Count (CCDF)":"Count", gpsLog10XY, PowerFit, gpwLinesPoints);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::PlotSccDistr	(	const PGraph &	Graph,
		const TStr &	FNmPref,
		TStr	DescStr = TStr()
	)

Plots the distribution of sizes of strongly connected components of a Graph.

Definition at line 98 of file statplot.h.

References TGnuPlot::AddPlot(), TStr::CStr(), TStr::Empty(), TStr::Fmt(), GetSccSzCnt(), gpsLog10XY, gpwLinesPoints, and TVec< TVal, TSizeTy >::Last().

                                                                          {
  TIntPrV SccSzCnt;
  TSnap::GetSccSzCnt(Graph, SccSzCnt);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot GnuPlot("scc."+FNmPref, TStr::Fmt("%s. G(%d, %d). Largest component has %f nodes",
    DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges(), SccSzCnt.Last().Val1/double(Graph->GetNodes())));
  GnuPlot.AddPlot(SccSzCnt, gpwLinesPoints, "", "pt 6");
  GnuPlot.SetXYLabel("Size of strongly connected component", "Number of components");
  GnuPlot.SetScale(gpsLog10XY);
  GnuPlot.SavePng();
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::PlotShortPathDistr	(	const PGraph &	Graph,
		const TStr &	FNmPref,
		TStr	DescStr = TStr(),
		int	TestNodes = TInt::Mx
	)

Plots the distribution of the shortest path lengths of a Graph. Implementation is based on BFS.

Definition at line 140 of file statplot.h.

References TVec< TVal, TSizeTy >::Add(), THash< TKey, TDat, THashFunc >::AddDat(), TSnap::TSnapDetail::CalcAvgDiamPdf(), TSnap::TSnapDetail::CalcEffDiamPdf(), TStr::CStr(), TBreathFS< PGraph >::DoBfs(), TStr::Empty(), TStr::Fmt(), THash< TKey, TDat, THashFunc >::GetKey(), gpsLog10Y, gpwLinesPoints, TVec< TVal, TSizeTy >::Last(), THash< TKey, TDat, THashFunc >::Len(), TMath::Mn(), TInt::Mx, TBreathFS< PGraph >::NIdDistH, TGnuPlot::PlotValV(), TInt::Rnd, TVec< TVal, TSizeTy >::Shuffle(), and THash< TKey, TDat, THashFunc >::SortByKey().

                                                                                               {
  TIntH DistToCntH;
  TBreathFS<PGraph> BFS(Graph);
  // shotest paths
  TIntV NodeIdV;
  Graph->GetNIdV(NodeIdV);  NodeIdV.Shuffle(TInt::Rnd);
  for (int tries = 0; tries < TMath::Mn(TestNodes, Graph->GetNodes()); tries++) {
    const int NId = NodeIdV[tries];
    BFS.DoBfs(NId, true, false, -1, TInt::Mx);
    for (int i = 0; i < BFS.NIdDistH.Len(); i++) {
      DistToCntH.AddDat(BFS.NIdDistH[i]) += 1; }
  }
  DistToCntH.SortByKey(true);
  TFltPrV DistNbrsPdfV;
  for (int i = 0; i < DistToCntH.Len(); i++) {
    DistNbrsPdfV.Add(TFltPr(DistToCntH.GetKey(i)(), DistToCntH[i]()));
  }
  const double EffDiam = TSnap::TSnapDetail::CalcEffDiamPdf(DistNbrsPdfV, 0.9);
  const double AvgDiam = TSnap::TSnapDetail::CalcAvgDiamPdf(DistNbrsPdfV);
  const int FullDiam = (int) DistNbrsPdfV.Last().Val1;
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot::PlotValV(DistNbrsPdfV, "diam."+FNmPref,
    TStr::Fmt("%s. G(%d, %d). Diam: avg:%.2f  eff:%.2f  max:%d", DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges(),
    AvgDiam, EffDiam, FullDiam), "Number of hops", "Number of shortest paths", gpsLog10Y, false, gpwLinesPoints);
}

Here is the call graph for this function:

void TSnap::PlotSngValDistr	(	const PNGraph &	Graph,
		const int &	SngVals,
		const TStr &	FNmPref,
		TStr	DescStr
	)

Plots the rank distribution of singular values of the Graph adjacency matrix. Plots first SngVals values.

Definition at line 58 of file statplot.cpp.

References THash< TKey, TDat, THashFunc >::AddDat(), TStr::CStr(), TStr::Empty(), TVec< TVal, TSizeTy >::Empty(), TStr::Fmt(), TNGraph::GetEdges(), THash< TKey, TDat, THashFunc >::GetKeyDatPrV(), TNGraph::GetNodes(), GetSngVals(), gpsAuto, gpwLinesPoints, TVec< TVal, TSizeTy >::Last(), TVec< TVal, TSizeTy >::Len(), TGnuPlot::PlotValV(), and TVec< TVal, TSizeTy >::Sort().

                                                                                                  {
  const int NBuckets = 50;
  TFltV SngValV;
  for (int f = 1; SngValV.Empty() && f < 4; f++) {
    TSnap::GetSngVals(Graph, f*SngVals, SngValV);
  }
  SngValV.Sort(true);
  THash<TFlt, TFlt> BucketCntH;
  double Step = (SngValV.Last()-SngValV[0]) / double(NBuckets-1);
  for (int i = 0; i < NBuckets; i++) {
    BucketCntH.AddDat(SngValV[0]+Step*(i+0.5), 0);
  }
  for (int i = 0; i < SngValV.Len(); i++) {
    const int Bucket = (int) floor((SngValV[i]-SngValV[0]) / Step);
    BucketCntH[Bucket] += 1;
  }
  TFltPrV EigCntV;
  BucketCntH.GetKeyDatPrV(EigCntV);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot::PlotValV(EigCntV, "sngDistr."+FNmPref, TStr::Fmt("%s. G(%d, %d). Largest eig val = %f", DescStr.CStr(),
    Graph->GetNodes(), Graph->GetEdges(), SngValV.Last().Val), "Singular value", "Count", gpsAuto, false, gpwLinesPoints);
}

Here is the call graph for this function:

void TSnap::PlotSngValRank	(	const PNGraph &	Graph,
		const int &	SngVals,
		const TStr &	FNmPref,
		TStr	DescStr
	)

Plots the rank distribution of singular values of the Graph adjacency matrix. Plots first SngVals values.

Definition at line 49 of file statplot.cpp.

References TStr::CStr(), TStr::Empty(), TStr::Fmt(), TNGraph::GetEdges(), TNGraph::GetNodes(), GetSngVals(), gpsLog10XY, gpwLinesPoints, TGnuPlot::PlotValV(), and TVec< TVal, TSizeTy >::Sort().

                                                                                                 {
  TFltV SngValV;
  TSnap::GetSngVals(Graph, SngVals, SngValV);
  SngValV.Sort(false);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot::PlotValV(SngValV, "sngVal."+FNmPref, TStr::Fmt("%s. G(%d, %d). Largest eig val = %f",
    DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges(), SngValV[0].Val), "Rank", "Singular value", gpsLog10XY, false, gpwLinesPoints);
}

Here is the call graph for this function:

void TSnap::PlotSngVec	(	const PNGraph &	Graph,
		const TStr &	FNmPref,
		TStr	DescStr
	)

Plots the distribution of the values of the leading left singular vector of the Graph adjacency matrix. Plots first SngVals values.

Definition at line 81 of file statplot.cpp.

References TStr::CStr(), TStr::Empty(), TStr::Fmt(), TNGraph::GetEdges(), TNGraph::GetNodes(), GetSngVec(), gpsLog10XY, gpwLinesPoints, TGUtil::MakeExpBins(), TGnuPlot::PlotValV(), and TVec< TVal, TSizeTy >::Sort().

                                                                         {
  TFltV LeftSV, RightSV;
  TSnap::GetSngVec(Graph, LeftSV, RightSV);
  LeftSV.Sort(false);
  RightSV.Sort(false);
  TFltV BinV;
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGUtil::MakeExpBins(LeftSV, BinV, 1.01);
  TGnuPlot::PlotValV(BinV, "sngVecL."+FNmPref, TStr::Fmt("%s. G(%d, %d). Left signular vector",
    DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges()), "Rank", "Component of left singular vector", gpsLog10XY, false, gpwLinesPoints);
  TGnuPlot::PlotValV(BinV, "sngVecL."+FNmPref, TStr::Fmt("%s. G(%d, %d). Right signular vector",
    DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges()), "Rank", "Component of right singular vector", gpsLog10XY, false, gpwLinesPoints);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::PlotWccDistr	(	const PGraph &	Graph,
		const TStr &	FNmPref,
		TStr	DescStr = TStr()
	)

Plots the distribution of sizes of weakly connected components of a Graph.

Definition at line 85 of file statplot.h.

References TGnuPlot::AddPlot(), TStr::CStr(), TStr::Empty(), TStr::Fmt(), GetWccSzCnt(), gpsLog10XY, gpwLinesPoints, and TVec< TVal, TSizeTy >::Last().

                                                                          {
  TIntPrV WccSzCnt;
  TSnap::GetWccSzCnt(Graph, WccSzCnt);
  if (DescStr.Empty()) { DescStr = FNmPref; }
  TGnuPlot GnuPlot("wcc."+FNmPref, TStr::Fmt("%s. G(%d, %d). Largest component has %f nodes",
    DescStr.CStr(), Graph->GetNodes(), Graph->GetEdges(), WccSzCnt.Last().Val1/double(Graph->GetNodes())));
  GnuPlot.AddPlot(WccSzCnt, gpwLinesPoints, "", "pt 6");
  GnuPlot.SetXYLabel("Size of weakly connected component", "Number of components");
  GnuPlot.SetScale(gpsLog10XY);
  GnuPlot.SavePng();
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::PrintInfo	(	const PGraph &	Graph,
		const TStr &	Desc = "",
		const TStr &	OutFNm = "",
		const bool &	Fast = true
	)

Prints basic graph statistics.

Parameters

Fast	true: only computes basic statistics (that can be computed fast). For more extensive information (and longer execution times) set Fast = false.

Definition at line 84 of file gbase.h.

References THash< TKey, TDat, THashFunc >::AddKey(), TStr::CStr(), TStr::Empty(), GetBfsEffDiam(), GetFlagStr(), TInt::GetMn(), TInt::GetMx(), GetMxSccSz(), GetMxWccSz(), TUInt64::GetStr(), GetTriads(), gfMx, gfUndef, HasGraphFlag, and THash< TKey, TDat, THashFunc >::Len().

Referenced by main(), and TKronMomentsFit::Test().

                                                                                            {
  int BiDirEdges=0, ZeroNodes=0, ZeroInNodes=0, ZeroOutNodes=0, SelfEdges=0, NonZIODegNodes=0;
  THash<TIntPr, TInt> UniqDirE, UniqUnDirE;
  FILE *F = stdout;
  if (! OutFNm.Empty()) F = fopen(OutFNm.CStr(), "wt");
  if (! Desc.Empty()) { fprintf(F, "%s:", Desc.CStr()); }
  else { fprintf(F, "Graph:"); }
  for (int f = gfUndef; f < gfMx; f++) {
    if (HasGraphFlag(typename PGraph::TObj, TGraphFlag(f))) {
      fprintf(F, " %s", TSnap::GetFlagStr(TGraphFlag(f)).CStr()); }
  }
  // calc stat
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetDeg()==0) ZeroNodes++;
    if (NI.GetInDeg()==0) ZeroInNodes++;
    if (NI.GetOutDeg()==0) ZeroOutNodes++;
    if (NI.GetInDeg()!=0 && NI.GetOutDeg()!=0) NonZIODegNodes++;
    if (! Fast || Graph->GetNodes() < 1000) {
      const int NId = NI.GetId();
      for (int edge = 0; edge < NI.GetOutDeg(); edge++) {
        const int DstNId = NI.GetOutNId(edge);
        if (Graph->IsEdge(DstNId, NId)) BiDirEdges++;
        if (NId == DstNId) SelfEdges++;
        UniqDirE.AddKey(TIntPr(NId, DstNId));
        UniqUnDirE.AddKey(TIntPr(TInt::GetMn(NId, DstNId), TInt::GetMx(NId, DstNId)));
      }
    }
  }
  int64 Closed=0, Open=0;
  double WccSz=0, SccSz=0;
  double EffDiam=0;
  int FullDiam=0;
  if (! Fast) {
    TSnap::GetTriads(Graph, Closed, Open);
    WccSz = TSnap::GetMxWccSz(Graph);
    SccSz = TSnap::GetMxSccSz(Graph);
    TSnap::GetBfsEffDiam(Graph, 100, false, EffDiam, FullDiam);
  }
  // print info
  fprintf(F, "\n");
  fprintf(F, "  Nodes:                    %d\n", Graph->GetNodes());
  fprintf(F, "  Edges:                    %d\n", Graph->GetEdges());
  fprintf(F, "  Zero Deg Nodes:           %d\n", ZeroNodes);
  fprintf(F, "  Zero InDeg Nodes:         %d\n", ZeroInNodes);
  fprintf(F, "  Zero OutDeg Nodes:        %d\n", ZeroOutNodes);
  fprintf(F, "  NonZero In-Out Deg Nodes: %d\n", NonZIODegNodes);
  if (! Fast) {
    fprintf(F, "  Unique directed edges:    %d\n", UniqDirE.Len());
    fprintf(F, "  Unique undirected edges:  %d\n", UniqUnDirE.Len());
    fprintf(F, "  Self Edges:               %d\n", SelfEdges);
    fprintf(F, "  BiDir Edges:              %d\n", BiDirEdges);
    fprintf(F, "  Closed triangles:         %s\n", TUInt64::GetStr(Closed).CStr());
    fprintf(F, "  Open triangles:           %s\n", TUInt64::GetStr(Open).CStr());
    fprintf(F, "  Frac. of closed triads:   %f\n", Closed/double(Closed+Open));
    fprintf(F, "  Connected component size: %f\n", WccSz);
    fprintf(F, "  Strong conn. comp. size:  %f\n", SccSz);
    fprintf(F, "  Approx. full diameter:    %d\n", FullDiam);
    fprintf(F, "  90%% effective diameter:  %f\n", EffDiam);
    //fprintf(F, "  Core\tNodes\tEdges\n");
    //for (int i  = 0; i < CNodesV.Len(); i++) {
    //  printf("  %d\t%d\t%d\n", CNodesV[i].Val1(), CNodesV[i].Val2(), CEdgesV[i].Val2());
    //}
  }
  if (! OutFNm.Empty()) { fclose(F); }
}

Here is the call graph for this function:

Here is the caller graph for this function:

int TSnap::PushRelabel	(	TPRManager &	PRM,
		const int &	NId,
		const TNEANet::TNodeI &	NI
	)

Returns the ID of the neighbor that NId pushes to, -1 if no push was made.

Definition at line 328 of file flow.cpp.

References TSnap::TPRManager::Capacity(), TSnap::TPRManager::EdgeNum(), TSnap::TPRManager::Flow(), TNEANet::TNodeI::GetDeg(), TNEANet::TNodeI::GetInDeg(), TNEANet::TNodeI::GetInEId(), TNEANet::TNodeI::GetInNId(), TNEANet::TNodeI::GetOutEId(), TNEANet::TNodeI::GetOutNId(), TSnap::TPRManager::Label(), PushToInNbr(), PushToOutNbr(), and Relabel().

Referenced by GetMaxFlowIntPR().

                                                                           {
  int EdgeN = PRM.EdgeNum(NId);
  int EId = -1, NbrNId = -1, ResFlow = 0;
  int Cutoff = NI.GetInDeg();
  if (EdgeN < Cutoff) {
    EId = NI.GetInEId(EdgeN);
    NbrNId = NI.GetInNId(EdgeN);
    ResFlow = PRM.Flow(EId);
  } else {
    EId = NI.GetOutEId(EdgeN - Cutoff);
    NbrNId = NI.GetOutNId(EdgeN - Cutoff);
    ResFlow = PRM.Capacity(EId) - PRM.Flow(EId);
  }
  if (ResFlow > 0 && PRM.Label(NId) - 1 == PRM.Label(NbrNId)) {
    if (EdgeN < Cutoff) {
      PushToInNbr(PRM, NId, NbrNId, EId);
    } else {
      PushToOutNbr(PRM, NId, NbrNId, EId);
    }
    return NbrNId;
  }
  if (EdgeN + 1 == NI.GetDeg()) {
    PRM.EdgeNum(NId) = 0;
    Relabel(PRM, NId, NI);
  } else {
    PRM.EdgeNum(NId)++;
  }
  return -1;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSnap::PushToInNbr	(	TPRManager &	PRM,
		const int &	NId,
		const int &	InNId,
		const int &	EId
	)

Returns flow from a node NId to a neighbor InNId over edge EId.

Definition at line 297 of file flow.cpp.

References TSnap::TPRManager::Excess(), TSnap::TPRManager::Flow(), and min.

Referenced by PushRelabel().

                                                                                     {
  int MinPush = min(PRM.Flow(EId), PRM.Excess(NId));
  PRM.Flow(EId) -= MinPush;
  PRM.Excess(NId) -= MinPush;
  PRM.Excess(InNId) += MinPush;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSnap::PushToOutNbr	(	TPRManager &	PRM,
		const int &	NId,
		const int &	OutNId,
		const int &	EId
	)

Pushes flow from a node NId to a neighbor OutNId over edge EId.

Definition at line 289 of file flow.cpp.

References TSnap::TPRManager::Capacity(), TSnap::TPRManager::Excess(), TSnap::TPRManager::Flow(), and min.

Referenced by PushRelabel().

                                                                                       {
  int MinPush = min(PRM.Capacity(EId) - PRM.Flow(EId), PRM.Excess(NId));
  PRM.Flow(EId) += MinPush;
  PRM.Excess(NId) -= MinPush;
  PRM.Excess(OutNId) += MinPush;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSnap::Relabel	(	TPRManager &	PRM,
		const int &	NId,
		const TNEANet::TNodeI &	NI
	)

Increases the label of a node NId to allow valid pushes to some neighbor.

Definition at line 305 of file flow.cpp.

References TSnap::TPRManager::Capacity(), TSnap::TPRManager::Flow(), TNEANet::TNodeI::GetInDeg(), TNEANet::TNodeI::GetInEId(), TNEANet::TNodeI::GetInNId(), TSnap::TPRManager::GetMaxLabel(), TNEANet::TNodeI::GetOutDeg(), TNEANet::TNodeI::GetOutEId(), TNEANet::TNodeI::GetOutNId(), TSnap::TPRManager::Label(), min, and TSnap::TPRManager::SetLabel().

Referenced by PushRelabel().

                                                                        {
  int MaxLabel = PRM.GetMaxLabel();
  int MinLabel = MaxLabel;
  for (int EdgeN = 0; EdgeN < NI.GetInDeg(); EdgeN++) {
    if (PRM.Flow(NI.GetInEId(EdgeN)) > 0) {
      int InLabel = PRM.Label(NI.GetInNId(EdgeN));
      MinLabel = min(MinLabel, InLabel);
    }
  }
  for (int EdgeN = 0; EdgeN < NI.GetOutDeg(); EdgeN++) {
    if (PRM.Capacity(NI.GetOutEId(EdgeN)) > PRM.Flow(NI.GetOutEId(EdgeN))) {
      int OutLabel = PRM.Label(NI.GetOutNId(EdgeN));
      MinLabel = min(MinLabel, OutLabel);
    }
  }
  if (MinLabel == MaxLabel) {
    PRM.SetLabel(NId, MaxLabel);
  } else {
    PRM.SetLabel(NId, MinLabel + 1);
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::SaveEdgeList	(	const PGraph &	Graph,
		const TStr &	OutFNm,
		const TStr &	Desc = TStr()
	)

Saves a graph into a text file. Each line contains two columns and encodes a single edge: <source node="" id>=""><tab><destination node="" id>="">

Definition at line 227 of file gio.h.

References TStr::CStr(), TStr::Empty(), gfDirected, and HasGraphFlag.

Referenced by main().

                                                                             {
  FILE *F = fopen(OutFNm.CStr(), "wt");
  if (HasGraphFlag(typename PGraph::TObj, gfDirected)) { fprintf(F, "# Directed graph: %s \n", OutFNm.CStr()); } 
  else { fprintf(F, "# Undirected graph (each unordered pair of nodes is saved once): %s\n", OutFNm.CStr()); }
  if (! Desc.Empty()) { fprintf(F, "# %s\n", Desc.CStr()); }
  fprintf(F, "# Nodes: %d Edges: %d\n", Graph->GetNodes(), Graph->GetEdges());
  if (HasGraphFlag(typename PGraph::TObj, gfDirected)) { fprintf(F, "# FromNodeId\tToNodeId\n"); }
  else { fprintf(F, "# NodeId\tNodeId\n"); }
  for (typename PGraph::TObj::TEdgeI ei = Graph->BegEI(); ei < Graph->EndEI(); ei++) {
    fprintf(F, "%d\t%d\n", ei.GetSrcNId(), ei.GetDstNId());
  }
  fclose(F);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::SaveGViz	(	const PGraph &	Graph,
		const TStr &	OutFNm,
		const TStr &	Desc = TStr(),
		const bool &	NodeLabels = false,
		const TIntStrH &	NIdColorH = TIntStrH()
	)

Save a graph in GraphVizp .DOT format.

Save a graph in GraphVizp .DOT format.

Parameters

NIdColorH

Maps node ids to node colors (see GraphViz documentation for more details).

Definition at line 369 of file gio.h.

References TStr::CStr(), TStr::Empty(), THash< TKey, TDat, THashFunc >::GetDat(), gfDirected, HasGraphFlag, and THash< TKey, TDat, THashFunc >::IsKey().

Referenced by DrawGViz().

                                                                                                                            {
  const bool IsDir = HasGraphFlag(typename PGraph::TObj, gfDirected);
  FILE *F = fopen(OutFNm.CStr(), "wt");
  if (! Desc.Empty()) fprintf(F, "/*****\n%s\n*****/\n\n", Desc.CStr());
  if (IsDir) { fprintf(F, "digraph G {\n"); } else { fprintf(F, "graph G {\n"); }
  fprintf(F, "  graph [splines=false overlap=false]\n"); //size=\"12,10\" ratio=fill
  // node  [width=0.3, height=0.3, label=\"\", style=filled, color=black]
  // node  [shape=box, width=0.3, height=0.3, label=\"\", style=filled, fillcolor=red]
  fprintf(F, "  node  [shape=ellipse, width=0.3, height=0.3%s]\n", NodeLabels?"":", label=\"\"");
  // node colors
  //for (int i = 0; i < NIdColorH.Len(); i++) {
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NIdColorH.IsKey(NI.GetId())) {
      fprintf(F, "  %d [style=filled, fillcolor=\"%s\"];\n", NI.GetId(), NIdColorH.GetDat(NI.GetId()).CStr()); }
    else {
      fprintf(F, "  %d ;\n", NI.GetId());
    }
  }
  // edges
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetOutDeg()==0 && NI.GetInDeg()==0 && !NIdColorH.IsKey(NI.GetId())) {
      fprintf(F, "%d;\n", NI.GetId()); }
    else {
      for (int e = 0; e < NI.GetOutDeg(); e++) {
        if (! IsDir && NI.GetId() > NI.GetOutNId(e)) { continue; }
        fprintf(F, "  %d %s %d;\n", NI.GetId(), IsDir?"->":"--", NI.GetOutNId(e));
      }
    }
  }
  if (! Desc.Empty()) {
    fprintf(F, "  label = \"\\n%s\\n\";", Desc.CStr());
    fprintf(F, "  fontsize=24;\n");
  }
  fprintf(F, "}\n");
  fclose(F);
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PGraph >

void TSnap::SaveGViz	(	const PGraph &	Graph,
		const TStr &	OutFNm,
		const TStr &	Desc,
		const TIntStrH &	NIdLabelH
	)

Save a graph in GraphVizp .DOT format.

Save a graph in GraphVizp .DOT format.

Parameters

NIdLabelH

Maps node ids to node string labels.

Definition at line 407 of file gio.h.

References TStr::CStr(), TStr::Empty(), THash< TKey, TDat, THashFunc >::GetDat(), gfDirected, and THash< TKey, TDat, THashFunc >::IsKey().

                                                                                                    {
  const bool IsDir = Graph->HasFlag(gfDirected);
  FILE *F = fopen(OutFNm.CStr(), "wt");
  if (! Desc.Empty()) fprintf(F, "/*****\n%s\n*****/\n\n", Desc.CStr());
  if (IsDir) { fprintf(F, "digraph G {\n"); } else { fprintf(F, "graph G {\n"); }
  fprintf(F, "  graph [splines=true overlap=false]\n"); //size=\"12,10\" ratio=fill
  fprintf(F, "  node  [shape=ellipse, width=0.3, height=0.3]\n");
  // node colors
  //for (int i = 0; i < NodeLabelH.Len(); i++) {
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    fprintf(F, "  %d [label=\"%s\"];\n", NI.GetId(), NIdLabelH.GetDat(NI.GetId()).CStr());
}
  // edges
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    if (NI.GetOutDeg()==0 && NI.GetInDeg()==0 && ! NIdLabelH.IsKey(NI.GetId())) {
      fprintf(F, "%d;\n", NI.GetId()); }
    else {
      for (int e = 0; e < NI.GetOutDeg(); e++) {
        if (! IsDir && NI.GetId() > NI.GetOutNId(e)) { continue; }
        fprintf(F, "  %d %s %d;\n", NI.GetId(), IsDir?"->":"--", NI.GetOutNId(e));
      }
    }
  }
  if (! Desc.Empty()) {
    fprintf(F, "  label = \"\\n%s\\n\";", Desc.CStr());
    fprintf(F, "  fontsize=24;\n");
  }
  fprintf(F, "}\n");
  fclose(F);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::SaveMatlabSparseMtx	(	const PGraph &	Graph,
		const TStr &	OutFNm
	)

Saves a graph in a MATLAB sparse matrix format.

Each line contains a tuple of 3 values: <source node="" id>=""><tab><destination node="" id>=""><tab>1.

Definition at line 351 of file gio.h.

References THashSet< TKey, THashFunc >::AddKey(), TStr::CStr(), gfDirected, and HasGraphFlag.

                                                                  {
  FILE *F = fopen(OutFNm.CStr(), "wt");
  TIntSet NIdSet(Graph->GetNodes()); // so that
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
    NIdSet.AddKey(NI.GetId());
  }
  for (typename PGraph::TObj::TEdgeI EI = Graph->BegEI(); EI < Graph->EndEI(); EI++) {
    const int Src = NIdSet.GetKeyId(EI.GetSrcNId())+1;
    const int Dst = NIdSet.GetKeyId(EI.GetDstNId())+1;
    fprintf(F, "%d\t%d\t1\n", Src, Dst);
    if (! HasGraphFlag(typename PGraph::TObj, gfDirected) && Src!=Dst) {
      fprintf(F, "%d\t%d\t1\n", Dst, Src);
    }
  }
  fclose(F);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::SavePajek	(	const PGraph &	Graph,
		const TStr &	OutFNm
	)

Saves a graph in a Pajek .NET format.

Definition at line 242 of file gio.h.

References THash< TKey, TDat, THashFunc >::AddDat(), TStr::CStr(), gfDirected, and HasGraphFlag.

                                                        {
  TIntH NIdToIdH(Graph->GetNodes(), true);
  FILE *F = fopen(OutFNm.CStr(), "wt");
  fprintf(F, "*Vertices %d\n", Graph->GetNodes());
  int i = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++, i++) {
    fprintf(F, "%d  \"%d\" ic Red fos 10\n", i+1, NI.GetId()); // ic: internal color, fos: font size
    NIdToIdH.AddDat(NI.GetId(), i+1);
  }
  if (HasGraphFlag(typename PGraph::TObj, gfDirected)) {
    fprintf(F, "*Arcs %d\n", Graph->GetEdges()); } // arcs are directed, edges are undirected
  else {
    fprintf(F, "*Edges %d\n", Graph->GetEdges());
  }
  for (typename PGraph::TObj::TEdgeI EI = Graph->BegEI(); EI < Graph->EndEI(); EI++) {
    const int SrcNId = NIdToIdH.GetDat(EI.GetSrcNId());
    const int DstNId = NIdToIdH.GetDat(EI.GetDstNId());
    fprintf(F, "%d %d %d c Black\n", SrcNId, DstNId, 1); // width=1
  }
  fclose(F);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::SavePajek	(	const PGraph &	Graph,
		const TStr &	OutFNm,
		const TIntStrH &	NIdColorH
	)

Saves a graph in a Pajek .NET format.

NIdColorH maps node ids to node colors. Default node color is Red. See http://vlado.fmf.uni-lj.si/pub/networks/pajek/doc/pajekman.pdf for a list of supported color names.

Definition at line 267 of file gio.h.

References THash< TKey, TDat, THashFunc >::AddDat(), TStr::CStr(), THash< TKey, TDat, THashFunc >::GetDat(), gfDirected, HasGraphFlag, and THash< TKey, TDat, THashFunc >::IsKey().

                                                                                   {
  TIntH NIdToIdH(Graph->GetNodes(), true);
  FILE *F = fopen(OutFNm.CStr(), "wt");
  fprintf(F, "*Vertices %d\n", Graph->GetNodes());
  int i = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++, i++) {
    fprintf(F, "%d  \"%d\" ic %s fos 10\n", i+1, NI.GetId(),
      NIdColorH.IsKey(NI.GetId()) ? NIdColorH.GetDat(NI.GetId()).CStr() : "Red");
    NIdToIdH.AddDat(NI.GetId(), i+1);
  }
  if (HasGraphFlag(typename PGraph::TObj, gfDirected)) {
    fprintf(F, "*Arcs %d\n", Graph->GetEdges()); } // arcs are directed, edges are undirected
  else {
    fprintf(F, "*Edges %d\n", Graph->GetEdges());
  }
  for (typename PGraph::TObj::TEdgeI EI = Graph->BegEI(); EI < Graph->EndEI(); EI++) {
    const int SrcNId = NIdToIdH.GetDat(EI.GetSrcNId());
    const int DstNId = NIdToIdH.GetDat(EI.GetDstNId());
    fprintf(F, "%d %d %d c Black\n", SrcNId, DstNId, 1);
  }
  fclose(F);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::SavePajek	(	const PGraph &	Graph,
		const TStr &	OutFNm,
		const TIntStrH &	NIdColorH,
		const TIntStrH &	NIdLabelH
	)

Saves a graph in a Pajek .NET format.

NIdColorH maps node ids to node colors. Default node color is Red. NIdLabelH maps node ids to node string labels. See http://vlado.fmf.uni-lj.si/pub/networks/pajek/doc/pajekman.pdf for a list of supported color names.

Definition at line 294 of file gio.h.

References THash< TKey, TDat, THashFunc >::AddDat(), TStr::CStr(), TStr::Fmt(), THash< TKey, TDat, THashFunc >::GetDat(), gfDirected, HasGraphFlag, and THash< TKey, TDat, THashFunc >::IsKey().

                                                                                                              {
  TIntH NIdToIdH(Graph->GetNodes(), true);
  FILE *F = fopen(OutFNm.CStr(), "wt");
  fprintf(F, "*Vertices %d\n", Graph->GetNodes());
  int i = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++, i++) {
    fprintf(F, "%d  \"%s\" ic %s fos 10\n", i+1,
      NIdLabelH.IsKey(NI.GetId()) ? NIdLabelH.GetDat(NI.GetId()).CStr() : TStr::Fmt("%d", NI.GetId()).CStr(),
      NIdColorH.IsKey(NI.GetId()) ? NIdColorH.GetDat(NI.GetId()).CStr() : "Red");
    NIdToIdH.AddDat(NI.GetId(), i+1);
  }
  if (HasGraphFlag(typename PGraph::TObj, gfDirected)) {
    fprintf(F, "*Arcs %d\n", Graph->GetEdges()); } // arcs are directed, edges are undirected
  else {
    fprintf(F, "*Edges %d\n", Graph->GetEdges());
  }
  for (typename PGraph::TObj::TEdgeI EI = Graph->BegEI(); EI < Graph->EndEI(); EI++) {
    const int SrcNId = NIdToIdH.GetDat(EI.GetSrcNId());
    const int DstNId = NIdToIdH.GetDat(EI.GetDstNId());
    fprintf(F, "%d %d %d c Black\n", SrcNId, DstNId, 1);
  }
  fclose(F);
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::SavePajek	(	const PGraph &	Graph,
		const TStr &	OutFNm,
		const TIntStrH &	NIdColorH,
		const TIntStrH &	NIdLabelH,
		const TIntStrH &	EIdColorH
	)

Saves a graph in a Pajek .NET format.

NIdColorH maps node ids to node colors. Default node color is Red. NIdLabelH maps node ids to node string labels. EIdColorH maps edge ids to node colors. Default edge color is Black. See http://vlado.fmf.uni-lj.si/pub/networks/pajek/doc/pajekman.pdf for a list of supported color names.

Definition at line 323 of file gio.h.

References THash< TKey, TDat, THashFunc >::AddDat(), CAssert, TStr::CStr(), TStr::Fmt(), THash< TKey, TDat, THashFunc >::GetDat(), gfDirected, gfMultiGraph, HasGraphFlag, and THash< TKey, TDat, THashFunc >::IsKey().

                                                                                                                                         {
  CAssert(HasGraphFlag(typename PGraph::TObj, gfMultiGraph)); // network needs to have edge ids
  TIntH NIdToIdH(Graph->GetNodes(), true);
  FILE *F = fopen(OutFNm.CStr(), "wt");
  fprintf(F, "*Vertices %d\n", Graph->GetNodes());
  int i = 0;
  for (typename PGraph::TObj::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++, i++) {
    fprintf(F, "%d  \"%s\" ic %s fos 10\n", i+1,
      NIdLabelH.IsKey(NI.GetId()) ? NIdLabelH.GetDat(NI.GetId()).CStr() : TStr::Fmt("%d", NI.GetId()).CStr(),
      NIdColorH.IsKey(NI.GetId()) ? NIdColorH.GetDat(NI.GetId()).CStr() : "Red");
    NIdToIdH.AddDat(NI.GetId(), i+1);
  }
  if (HasGraphFlag(typename PGraph::TObj, gfDirected)) {
    fprintf(F, "*Arcs %d\n", Graph->GetEdges()); } // arcs are directed, edges are undirected
  else {
    fprintf(F, "*Edges %d\n", Graph->GetEdges());
  }
  for (typename PGraph::TObj::TEdgeI EI = Graph->BegEI(); EI < Graph->EndEI(); EI++) {
    const int SrcNId = NIdToIdH.GetDat(EI.GetSrcNId());
    const int DstNId = NIdToIdH.GetDat(EI.GetDstNId());
    fprintf(F, "%d %d 1 c %s\n", SrcNId, DstNId,
      EIdColorH.IsKey(EI.GetId()) ? EIdColorH.GetDat(EI.GetId()).CStr() : "Black");
  }
  fclose(F);
}

Here is the call graph for this function:

void TSnap::SetAllInvertSign	(	TFltV &	ValV,
		const double &	Val
	)

Definition at line 158 of file gsvd.cpp.

References TVec< TVal, TSizeTy >::Len().

                                                      {
  for (int i = 0; i < ValV.Len(); i++) { 
    ValV[i] = -ValV[i]; 
  }
}

Here is the call graph for this function:

template<class PGraph >

void TSnap::TestAnf

(

)

Definition at line 241 of file anf.h.

References TVec< TVal, TSizeTy >::Add(), TGraphAnf< PGraph >::GetGraphAnf(), TMom::GetMean(), TMom::GetSDev(), TVec< TVal, TSizeTy >::Last(), and TVec< TVal, TSizeTy >::Len().

                                       {
  PGraph Graph = PGraph::TObj::New();
  //Graph:
  //  0    2 ----> 3
  //       ^       |
  //       |       |
  //       |       ^
  //  1    5 <---- 4
  for (int v = 0; v < 6; v++) { Graph->AddNode(v); }
  Graph->AddEdge(2, 3);
  Graph->AddEdge(3, 4);
  Graph->AddEdge(4, 5);
  Graph->AddEdge(5, 2);
  TFltV AnfV;
  for (int t = 0; t < 10; t++) {
    TGraphAnf<PGraph> Anf(Graph, 128, 5, t+1);
    TIntFltKdV DistToNbrsV;
    Anf.GetGraphAnf(DistToNbrsV, 5, true);
    printf("\n--seed: %d---------------------\n", t+1);
    for (int i = 0; i < DistToNbrsV.Len(); i++) {
      printf("dist: %d\t hops:%f\n", DistToNbrsV[i].Key(), DistToNbrsV[i].Dat());
    }
    AnfV.Add(DistToNbrsV.Last().Dat);
  }
  TMom Mom(AnfV);
  printf("-----------\nAvgAnf: %f  StDev:  %f\n", Mom.GetMean(), Mom.GetSDev());//*/
  // const int NApprox = 32;
  /*printf("\nANF vs. SAMPLE diam test (10 runs of ANF, NApprox=%d):\n", NApprox);
  //Graph = TGGen<PGraph>::GenGrid(20, 20);
  Graph = TGAlg::GetMxWcc(TGGen<PGraph>::GenRnd(1000, 10000));
  TFltV FullAnf, EffAnf;
  for (int tryn = 0; tryn < 10; tryn++) {
    FullAnf.Add(GetEffDiam(Graph, false, 1.0, NApprox));
    EffAnf.Add(GetEffDiam(Graph, false, 0.9, NApprox));
  }
  TMom FullMom(FullAnf);
  TMom AnfMom(EffAnf);
  printf("  Sample FullDiam:      %d\n", TGAlg::GetBfsFullDiam(Graph, 100, false));
  printf("  Anf    FullDiam:      %f  [%f]\n", FullMom.GetMean(), FullMom.GetSDev());
  printf("  Sample EffDiam [90%%]: %f\n", TGAlg::GetBfsEffDiam(Graph, 100, false));
  printf("  Anf    EffDiam [90%%]: %f  [%f]\n", AnfMom.GetMean(), AnfMom.GetSDev());
  // epinions
  printf("\nEpinions graph:\n");
  { typedef PNGraph PGraph;
  PGraph G = TGGen<PGraph>::GenEpinions();
  TIntFltKdV DistToPairsV;
  GetAnf(G, DistToPairsV, 50, true);
  for(int i = 0; i < DistToPairsV.Len(); i++) {
    printf("\t%d\t%f\n", DistToPairsV[i].Key, DistToPairsV[i].Dat); }
  printf("\nUndir\n");
  TAnf<PGraph>::GetAnf(G, DistToPairsV, 50, false);
  for(int j = 0; j < DistToPairsV.Len(); j++) {
    printf("\t%d\t%f\n", DistToPairsV[j].Key, DistToPairsV[j].Dat); }
  }//*/
}

Here is the call graph for this function: