SNAP Library , Developer Reference  2013-01-07 14:03:36
SNAP, a general purpose, high performance system for analysis and manipulation of large networks
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Defines
Static Public Member Functions
TSpecFunc Class Reference

#include <xmath.h>

List of all members.

Static Public Member Functions

static void GammaPSeries (double &gamser, const double &a, const double &x, double &gln)
static void GammaQContFrac (double &gammcf, const double &a, const double &x, double &gln)
static double GammaQ (const double &a, const double &x)
static double LnGamma (const double &xx)
static double BetaCf (const double &a, const double &b, const double &x)
static double BetaI (const double &a, const double &b, const double &x)
static void LinearFit (const TVec< TFltPr > &XY, double &A, double &B, double &SigA, double &SigB, double &Chi2, double &R2)
static void PowerFit (const TVec< TFltPr > &XY, double &A, double &B, double &SigA, double &SigB, double &Chi2, double &R2)
static void LogFit (const TVec< TFltPr > &XY, double &A, double &B, double &SigA, double &SigB, double &Chi2, double &R2)
static void ExpFit (const TVec< TFltPr > &XY, double &A, double &B, double &SigA, double &SigB, double &Chi2, double &R2)
static double LnComb (const int &n, const int &k)
static double Entropy (const TIntV &ValV)
static double Entropy (const TFltV &ValV)
static void EntropyFracDim (const TIntV &ValV, TFltV &EntropyV)
static void EntropyFracDim (const TFltV &ValV, TFltV &EntropyV)
static double EntropyBias (const double &B)
static double GetPowerCoef (const TFltV &XValV, double MinX=-1.0)
static double GetPowerCoef (const TFltPrV &XValCntV, double MinX=-1.0)

Detailed Description

Definition at line 89 of file xmath.h.

Member Function Documentation

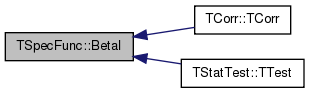
double TSpecFunc::BetaCf ( const double &  a,
const double &  b,
const double &  x 
) [static]

Definition at line 99 of file xmath.cpp.

References Fail.

Referenced by BetaI().

                                                                         {
  static const double MAXIT=100;
  static const double EPS=3.0e-7;
  static const double FPMIN=1.0e-30;
  int m,m2;
  double aa,c,d,del,h,qab,qam,qap;

  qab=a+b;
  qap=a+1.0;
  qam=a-1.0;
  c=1.0;
  d=1.0-qab*x/qap;
  if (fabs(d) < FPMIN) d=FPMIN;
  d=1.0/d;
  h=d;
  for (m=1;m<=MAXIT;m++) {
    m2=2*m;
    aa=m*(b-m)*x/((qam+m2)*(a+m2));
    d=1.0+aa*d;
    if (fabs(d) < FPMIN) d=FPMIN;
    c=1.0+aa/c;
    if (fabs(c) < FPMIN) c=FPMIN;
    d=1.0/d;
    h *= d*c;
    aa = -(a+m)*(qab+m)*x/((a+m2)*(qap+m2));
    d=1.0+aa*d;
    if (fabs(d) < FPMIN) d=FPMIN;
    c=1.0+aa/c;
    if (fabs(c) < FPMIN) c=FPMIN;
    d=1.0/d;
    del=d*c;
    h *= del;
    if (fabs(del-1.0) < EPS) break;
  }
  if (m > MAXIT){Fail;}// a or b too big, or MAXIT too small in betacf
  return h;
}

Here is the caller graph for this function:

double TSpecFunc::BetaI ( const double &  a,
const double &  b,
const double &  x 
) [static]

Definition at line 137 of file xmath.cpp.

References BetaCf(), Fail, and LnGamma().

Referenced by TCorr::TCorr(), and TStatTest::TTest().

                                                                        {
  double bt;

  if (x < 0.0 || x > 1.0){Fail;} // Bad x in routine betai
  if (x == 0.0 || x == 1.0) bt=0.0;
  else
    bt=exp(LnGamma(a+b)-LnGamma(a)-LnGamma(b)+a*log(x)+b*log(1.0-x));
  if (x < (a+1.0)/(a+b+2.0))
    return bt*BetaCf(a,b,x)/a;
  else
    return 1.0-bt*BetaCf(b,a,1.0-x)/b;
}

Here is the call graph for this function:

Here is the caller graph for this function:

double TSpecFunc::Entropy ( const TIntV &  ValV) [static]

Definition at line 231 of file xmath.cpp.

References TVec< TVal >::Len().

Referenced by EntropyFracDim().

                                           {
  TFltV NewValV(ValV.Len());
  for (int i = 0; i < ValV.Len(); i++) { NewValV[i] = ValV[i]; }
  return Entropy(NewValV);
}

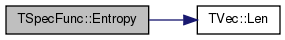
Here is the call graph for this function:

Here is the caller graph for this function:

double TSpecFunc::Entropy ( const TFltV &  ValV) [static]

Definition at line 238 of file xmath.cpp.

References TVec< TVal >::Len(), and TMath::LogOf2.

                                           {
  double Sum=0, Ent=0;
  for (int i = 0; i < ValV.Len(); i++) {
    const double& Val = ValV[i];
    if (Val > 0.0) { Ent -= Val * log(Val);  Sum += Val; }
  }
  if (Sum > 0.0) {
    Ent /= Sum;
    Ent += log(Sum);
    Ent /= TMath::LogOf2;
  } else return 1.0;
  return Ent;
}

Here is the call graph for this function:

double TSpecFunc::EntropyBias ( const double &  B) [static]

Definition at line 285 of file xmath.cpp.

References THash< TKey, TDat, THashFunc >::AddDat(), THash< TKey, TDat, THashFunc >::Empty(), THash< TKey, TDat, THashFunc >::GetDat(), THash< TKey, TDat, THashFunc >::IsKey(), and TMath::Round().

                                            {
  static TFltFltH BToP;
  if (BToP.Empty()) {
    for (double p = 0.5; p < 1.0; p +=0.0001) {
      double H = p * log(p) + (1.0-p) * log(1.0 - p);
      H = -H / log(2.0);
      BToP.AddDat(TMath::Round(H, 3), p);
    }
  }
  if (BToP.IsKey(TMath::Round(B, 3))) { return BToP.GetDat(TMath::Round(B, 3)); }
  else { return -1.0; }
}

Here is the call graph for this function:

void TSpecFunc::EntropyFracDim ( const TIntV &  ValV,
TFltV &  EntropyV 
) [static]

Definition at line 252 of file xmath.cpp.

References IAssert, and TVec< TVal >::Len().

                                                                 {
  TFltV NewValV(ValV.Len());
  for (int i = 0; i < ValV.Len(); i++) { 
    IAssert(ValV[i]==1 || ValV[i] == 0);
    NewValV[i] = ValV[i]; 
  }
  EntropyFracDim(NewValV, EntropyV);
}

Here is the call graph for this function:

void TSpecFunc::EntropyFracDim ( const TFltV &  ValV,
TFltV &  EntropyV 
) [static]

Definition at line 264 of file xmath.cpp.

References TVec< TVal >::Add(), TVec< TVal >::Clr(), Entropy(), TVec< TVal >::Gen(), IAssert, TVec< TVal >::Len(), TVec< TVal >::MoveFrom(), and TVec< TVal >::Reverse().

                                                                 {
  TFltV ValV1, ValV2;
  int Pow2 = 1;
  while (2*Pow2 <= ValV.Len()) { Pow2 *= 2; }
  ValV1.Gen(Pow2);
  for (int i = 0; i < Pow2; i++) { ValV1[i] = ValV[i]; 
    IAssert(ValV[i]==1.0 || ValV[i] == 0.0); }
  EntropyV.Clr();
  EntropyV.Add(Entropy(ValV1)); // 2^Pow2 windows
  while (ValV1.Len() > 2) {
    ValV2.Gen(ValV1.Len() / 2);
    for (int i = 0; i < ValV1.Len(); i++) {
      ValV2[i/2] += ValV1[i];
    }
    EntropyV.Add(Entropy(ValV2));
    ValV1.MoveFrom(ValV2);
  }
  EntropyV.Reverse();
}

Here is the call graph for this function:

void TSpecFunc::ExpFit ( const TVec< TFltPr > &  XY,
double &  A,
double &  B,
double &  SigA,
double &  SigB,
double &  Chi2,
double &  R2 
) [static]

Definition at line 218 of file xmath.cpp.

References TVec< TVal >::Add(), TVec< TVal >::Len(), and LinearFit().

Referenced by TGnuPlot::AddExpFit().

                                                       {
  // Y = A * exp(B*X)
  TFltPrV XLogY(XY.Len(), 0);
  double AA, BB;
  for (int s = 0; s < XY.Len(); s++) {
    XLogY.Add(TFltPr(XY[s].Val1, log((double)XY[s].Val2)));
  }
  TSpecFunc::LinearFit(XLogY, AA, BB, SigA, SigB, Chi2, R2);
  A = exp(AA);
  B = BB;
}

Here is the call graph for this function:

Here is the caller graph for this function:

void TSpecFunc::GammaPSeries ( double &  gamser,
const double &  a,
const double &  x,
double &  gln 
) [static]

Definition at line 9 of file xmath.cpp.

References Fail, and IAssert.

                                                               {
  static const int ITMAX=100;
  static const double EPS=3.0e-7;
  int n;
  double sum, del, ap;

  gln=LnGamma(a);
  if (x <= 0.0){
    IAssert(x>=0); /*if (x < 0.0) nrerror("x less than 0 in routine gser");*/
    gamser=0.0;
    return;
  } else {
    ap=a;
    del=sum=1.0/a;
    for (n=1; n<=ITMAX; n++){
      ++ap;
      del *= x/ap;
      sum += del;
      if (fabs(del) < fabs(sum)*EPS){
        gamser=sum*exp(-x+a*log(x)-(gln));
        return;
      }
    }
    Fail; /*nrerror("a too large, ITMAX too small in routine gser");*/
    return;
  }
}
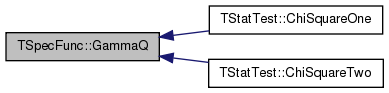
double TSpecFunc::GammaQ ( const double &  a,
const double &  x 
) [static]

Definition at line 68 of file xmath.cpp.

References IAssert.

Referenced by TStatTest::ChiSquareOne(), and TStatTest::ChiSquareTwo().

                                                         {
  IAssert((x>=0)&&(a>0));
  double gamser, gammcf, gln;
  if (x<(a+1.0)){
    GammaPSeries(gamser,a,x,gln);
    return 1.0-gamser;
  } else {
    GammaQContFrac(gammcf,a,x,gln);
    return gammcf;
  }
}

Here is the caller graph for this function:

void TSpecFunc::GammaQContFrac ( double &  gammcf,
const double &  a,
const double &  x,
double &  gln 
) [static]

Definition at line 38 of file xmath.cpp.

References IAssert.

                                                               {
  static const int ITMAX=100;
  static const double EPS=3.0e-7;
  static const double  FPMIN=1.0e-30;
  int i;
  double an, b, c, d, del, h;

  gln=LnGamma(a);
  b=x+1.0-a;
  c=1.0/FPMIN;
  d=1.0/b;
  h=d;
  for (i=1;i<=ITMAX;i++){
    an = -i*(i-a);
    b += 2.0;
    d=an*d+b;
    if (fabs(d) < FPMIN) d=FPMIN;
    c=b+an/c;
    if (fabs(c) < FPMIN) c=FPMIN;
    d=1.0/d;
    del=d*c;
    h *= del;
    if (fabs(del-1.0) < EPS) break;
  }
  IAssert(i<=ITMAX);
  /*if (i > ITMAX) nrerror("a too large, ITMAX too small in gcf");*/
  gammcf=exp(-x+a*log(x)-(gln))*h;
}
double TSpecFunc::GetPowerCoef ( const TFltV &  XValV,
double  MinX = -1.0 
) [static]

Definition at line 299 of file xmath.cpp.

References IAssert, and TVec< TVal >::Len().

Referenced by TGnuPlot::AddPwrFit2().

                                                              {
  for (int i = 0; MinX <= 0.0 && i < XValV.Len(); i++) { 
    MinX = XValV[i]; }
  IAssert(MinX > 0.0);
  double LnSum=0.0;
  for (int i = 0; i < XValV.Len(); i++) {
    if (XValV[i].Val < MinX) continue;
    LnSum += log(XValV[i] / MinX);
  }
  return 1.0 + double(XValV.Len()) / LnSum;
}

Here is the call graph for this function:

Here is the caller graph for this function:

double TSpecFunc::GetPowerCoef ( const TFltPrV &  XValCntV,
double  MinX = -1.0 
) [static]

Definition at line 311 of file xmath.cpp.

References IAssert, and TVec< TVal >::Len().

                                                                   {
  for (int i = 0; MinX <= 0.0 && i < XValCntV.Len(); i++) { 
    MinX = XValCntV[i].Val1; }
  IAssert(MinX > 0.0);
  double NSamples=0.0, LnSum=0.0;
  for (int i = 0; i < XValCntV.Len(); i++) {
    if (XValCntV[i].Val1() < MinX) continue;
    LnSum += XValCntV[i].Val2 * log(XValCntV[i].Val1 / MinX);
    NSamples += XValCntV[i].Val2;
  }
  return 1.0 + NSamples / LnSum;
}

Here is the call graph for this function:

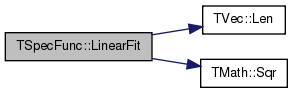
void TSpecFunc::LinearFit ( const TVec< TFltPr > &  XY,
double &  A,
double &  B,
double &  SigA,
double &  SigB,
double &  Chi2,
double &  R2 
) [static]

Definition at line 150 of file xmath.cpp.

References TVec< TVal >::Len(), and TMath::Sqr().

Referenced by TGnuPlot::AddLinFit(), ExpFit(), LogFit(), and PowerFit().

                                                       {
  // y = a + bx :: SigA (SigB): A's uncertainty; Chi2: std dev on all points
  int i;
  double t, sxoss, sx = 0.0, sy = 0.0, st2 = 0.0, ss, sigdat;

  A = B = SigA = SigB = Chi2 = 0.0;
  for (i = 0; i < XY.Len(); i++) {
    sx += XY[i].Val1;
    sy += XY[i].Val2;
  }
  ss = XY.Len();
  sxoss = sx / ss;
  for (i = 0; i <XY.Len(); i++) {
    t = XY[i].Val1 - sxoss;
    st2 += t*t;
    B += t * XY[i].Val2;
  }
  B /= st2;
  A = (sy - sx * B) / ss;
  SigA = sqrt((1.0 + sx * sx / (ss * st2)) / ss);
  SigB = sqrt(1.0 / st2);
  for (i = 0; i < XY.Len(); i++)
    Chi2 += TMath::Sqr(XY[i].Val2 - A - B * XY[i].Val1);
  sigdat = sqrt(Chi2 / (XY.Len() - 2));
  SigA *= sigdat;
  SigB *= sigdat;

  // calculate R squared
  { double N = XY.Len(), sXY=0.0, sX=0.0, sY=0.0, sSqX=0.0, sSqY=0.0;
  for (int s =0; s < XY.Len(); s++) {
    sX += XY[s].Val1;  sY += XY[s].Val2;
    sXY += XY[s].Val1 * XY[s].Val2;
    sSqX += TMath::Sqr(XY[s].Val1);
    sSqY += TMath::Sqr(XY[s].Val2);
  }
  R2 = TMath::Sqr(N*sXY - sX*sY) / ((N*sSqX - sX*sX) * (N*sSqY - sY*sY)); }
  if (1.1 < R2 || -1.1 > R2) R2 = 0.0;
  if (_isnan(A) || ! _finite(A)) A = 0.0;
  if (_isnan(B) || ! _finite(B)) B = 0.0;
}

Here is the call graph for this function:

Here is the caller graph for this function:

double TSpecFunc::LnComb ( const int &  n,
const int &  k 
) [static]

Definition at line 95 of file xmath.cpp.

References LnGamma().

                                                  {
  return LnGamma(n+1)-LnGamma(k+1)-LnGamma(n-k+1);
}

Here is the call graph for this function:

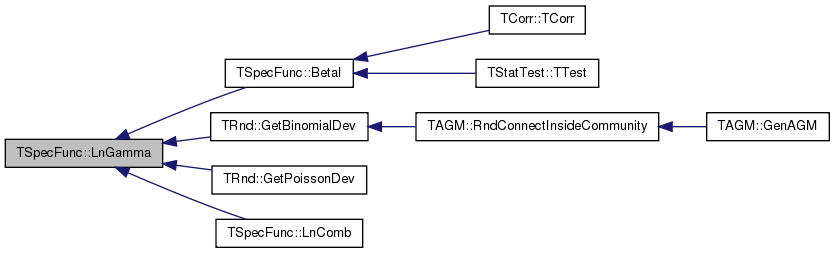
double TSpecFunc::LnGamma ( const double &  xx) [static]

Definition at line 80 of file xmath.cpp.

Referenced by BetaI(), TRnd::GetBinomialDev(), TRnd::GetPoissonDev(), and LnComb().

                                          {
  double x, y, tmp, ser;
  static double cof[6]={76.18009172947146,-86.50532032941677,
          24.01409824083091,-1.231739572450155,
          0.1208650973866179e-2,-0.5395239384953e-5};
  int j;

  y=x=xx;
  tmp=x+5.5;
  tmp -= (x+0.5)*log(tmp);
  ser=1.000000000190015;
  for (j=0;j<=5;j++) ser += cof[j]/++y;
  return -tmp+log(2.5066282746310005*ser/x);
}

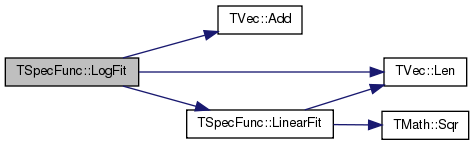
Here is the caller graph for this function:

void TSpecFunc::LogFit ( const TVec< TFltPr > &  XY,
double &  A,
double &  B,
double &  SigA,
double &  SigB,
double &  Chi2,
double &  R2 
) [static]

Definition at line 208 of file xmath.cpp.

References TVec< TVal >::Add(), TVec< TVal >::Len(), and LinearFit().

Referenced by TGnuPlot::AddLogFit().

                                                       {
  // Y = A + B*log(X)
  TFltPrV LogXY(XY.Len(), 0);
  for (int s = 0; s < XY.Len(); s++) {
    LogXY.Add(TFltPr(log((double)XY[s].Val1), XY[s].Val2));
  }
  TSpecFunc::LinearFit(LogXY, A, B, SigA, SigB, Chi2, R2);
}

Here is the call graph for this function:

Here is the caller graph for this function:

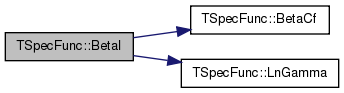
void TSpecFunc::PowerFit ( const TVec< TFltPr > &  XY,
double &  A,
double &  B,
double &  SigA,
double &  SigB,
double &  Chi2,
double &  R2 
) [static]

Definition at line 193 of file xmath.cpp.

References TVec< TVal >::Add(), TVec< TVal >::Len(), and LinearFit().

Referenced by TGnuPlot::AddPwrFit1(), TGnuPlot::AddPwrFit2(), and TGnuPlot::AddPwrFit3().

                                                       {
  // y = a x^b :: SigA (SigB): A's uncertainty; Chi2: std dev on all points
  // log fit
  double AA, BB;
  TFltPrV LogXY(XY.Len(), 0);
  for (int s = 0; s < XY.Len(); s++) {
    LogXY.Add(TFltPr(log((double)XY[s].Val1), log((double)XY[s].Val2)));
  }
  TSpecFunc::LinearFit(LogXY, AA, BB, SigA, SigB, Chi2, R2);
  A = exp(AA);  B = BB;
  if (_isnan(AA) || ! _finite(AA)) A = 0.0;
  if (_isnan(BB) || ! _finite(BB)) B = 0.0;
}

Here is the call graph for this function:

Here is the caller graph for this function:

The documentation for this class was generated from the following files: