|
SNAP Library , Developer Reference
2013-01-07 14:03:36
SNAP, a general purpose, high performance system for analysis and manipulation of large networks
|
|
SNAP Library , Developer Reference
2013-01-07 14:03:36
SNAP, a general purpose, high performance system for analysis and manipulation of large networks
|
#include <kronecker.h>
Public Member Functions | |
| TKronMomentsFit (const PUNGraph &G) | |
| TFltQu | EstABC (const int &R) |
Static Public Member Functions | |
| static void | Test () |
Public Attributes | |
| double | Edges |
| double | Hairpins |
| double | Tripins |
| double | Triads |
Definition at line 303 of file kronecker.h.
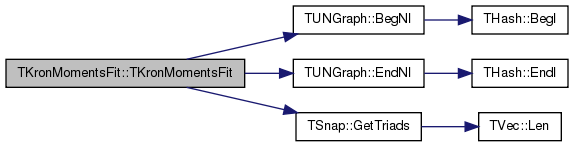
| TKronMomentsFit::TKronMomentsFit | ( | const PUNGraph & | G | ) | [inline] |
Definition at line 307 of file kronecker.h.
References TUNGraph::BegNI(), Edges, TUNGraph::EndNI(), TSnap::GetTriads(), Hairpins, Triads, and Tripins.
{
Edges=0; Hairpins=0; Tripins=0; Triads=0;
for (TUNGraph::TNodeI NI = G->BegNI(); NI < G->EndNI(); NI++) {
const int d = NI.GetOutDeg();
Edges += d;
Hairpins += d*(d-1.0);
Tripins += d*(d-1.0)*(d-2.0);
}
Edges /= 2.0;
Hairpins /= 2.0;
Tripins /= 6.0;
int ot,ct;
Triads = TSnap::GetTriads(G, ot, ct)/3.0;
printf("E:%g\tH:%g\tT:%g\tD:%g\n", Edges, Hairpins, Tripins, Triads);
}
| TFltQu TKronMomentsFit::EstABC | ( | const int & | R | ) | [inline] |
Definition at line 323 of file kronecker.h.
References Edges, Hairpins, TMath::IsInEps(), TFlt::Mx, Triads, and Tripins.
Referenced by Test().
{
const double Step = 0.01;
double MinScore=TFlt::Mx;
double A=0, B=0, C=0;
//Edges=log(Edges); Hairpins=log(Hairpins); Tripins=log(Tripins); Triads=log(Triads);
for (double a = 1.0; a > Step; a-=Step) {
for (double b = Step; b <= 1.0; b+=Step) {
for (double c = Step; c <= a; c+=Step) {
double EE = ( pow(a+2*b+c, R) - pow(a+c, R) ) / 2.0;
double EH = ( pow(pow(a+b,2) + pow(b+c,2), R)
-2*pow(a*(a+b)+c*(c+b), R)
-pow(a*a + 2*b*b + c*c, R)
+2*pow(a*a + c*c, R) ) / 2.0;
double ET = ( pow(pow(a+b,3)+pow(b+c,3), R)
-3*pow(a*pow(a+b,2)+c*pow(b+c,2), R)
-3*pow(a*a*a + c*c*c + b*(a*a+c*c) + b*b*(a+c) + 2*b*b*b ,R)
+2*pow(a*a*a + 2*b*b*b + c*c*c, R)
+5*pow(a*a*a + c*c*c + b*b*(a+c), R)
+4*pow(a*a*a + c*c*c + b*(a*a+c*c), R)
-6*pow(a*a*a + c*c*c, R) ) / 6.0;
double ED = ( pow(a*a*a + 3*b*b*(a+c) + c*c*c, R)
-3*pow(a*(a*a+b*b) + c*(b*b+c*c), R)
+2*pow(a*a*a+c*c*c, R) ) / 6.0;
if (EE < 0) { EE = 1; }
if (EH < 0) { EH = 1; }
if (ET < 0) { ET = 1; }
if (ED < 0) { ED = 1; }
//EE=log(EE); EH=log(EH); ET=log(ET); ED=log(ED);
double Score = pow(Edges-EE,2)/EE + pow(Hairpins-EH ,2)/EH + pow(Tripins-ET, 2)/ET + pow(Triads-ED, 2)/ED;
//double Score = fabs(Edges-EE)/EE + fabs(Hairpins-EH)/EH + fabs(Tripins-ET)/ET + fabs(Triads-ED)/ED;
//double Score = log(pow(Edges-EE,2)/EE) + log(pow(Hairpins-EH,2)/EH) + log(pow(Tripins-ET, 2)/ET) + log(pow(Triads-ED, 2)/ED);
if (MinScore > Score || (a==0.9 && b==0.6 && c==0.2) || (TMath::IsInEps(a-0.99,1e-6) && TMath::IsInEps(b-0.57,1e-6) && TMath::IsInEps(c-0.05,1e-6)))
{
printf("%.03f %.03f %0.03f %10.4f %10.10g\t%10.10g\t%10.10g\t%10.10g\n", a,b,c, log10(Score), EE, EH, ET, ED);
//printf("%.03f %.03f %0.03f %g\n", a,b,c, log(Score));
A=a; B=b; C=c; MinScore=Score;
}
}
}
}
printf("\t\t\t %10.10g\t%10.10g\t%10.10g\t%10.10g\n", Edges, Hairpins, Tripins, Triads);
return TFltQu(A,B,C,MinScore);
}
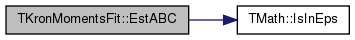

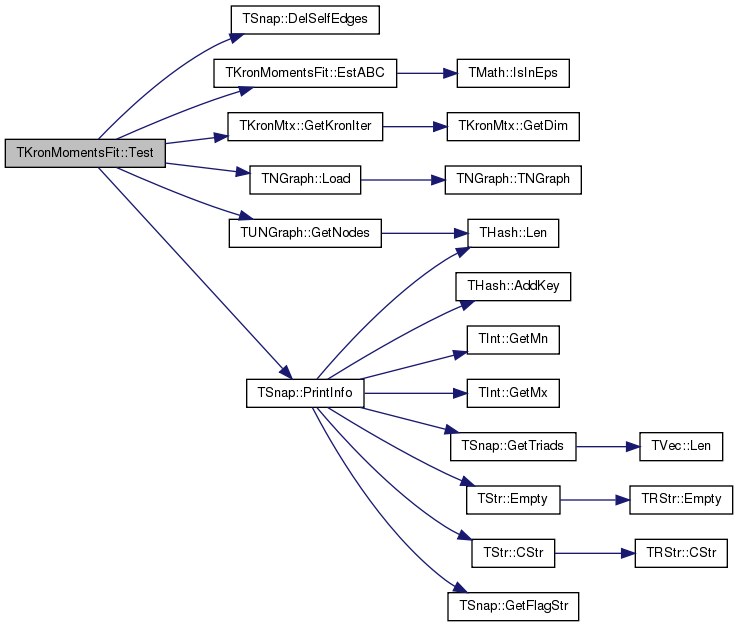
| static void TKronMomentsFit::Test | ( | ) | [inline, static] |
Definition at line 367 of file kronecker.h.
References TSnap::DelSelfEdges(), EstABC(), TKronMtx::GetKronIter(), TUNGraph::GetNodes(), TNGraph::Load(), and TSnap::PrintInfo().
{
TFIn FIn("as20.ngraph");
PUNGraph G = TSnap::ConvertGraph<PUNGraph>(TNGraph::Load(FIn));
//PUNGraph G = TKronMtx::GenFastKronecker(TKronMtx::GetMtx("0.9, 0.6; 0.6, 0.2"), 14, false, 0)->GetUNGraph();
//PUNGraph G = TUNGraph::GetSmallGraph();
TSnap::PrintInfo(G);
TSnap::DelSelfEdges(G);
TSnap::PrintInfo(G);
TKronMomentsFit Fit(G);
printf("iter %d\n", TKronMtx::GetKronIter(G->GetNodes(), 2));
Fit.EstABC(TKronMtx::GetKronIter(G->GetNodes(), 2)); //*/
}
| double TKronMomentsFit::Edges |
Definition at line 305 of file kronecker.h.
Referenced by EstABC(), and TKronMomentsFit().
| double TKronMomentsFit::Hairpins |
Definition at line 305 of file kronecker.h.
Referenced by EstABC(), and TKronMomentsFit().
| double TKronMomentsFit::Triads |
Definition at line 305 of file kronecker.h.
Referenced by EstABC(), and TKronMomentsFit().
| double TKronMomentsFit::Tripins |
Definition at line 305 of file kronecker.h.
Referenced by EstABC(), and TKronMomentsFit().