#include <exp.h>

Collaboration diagram for TExpBi:

Public Member Functions
	TExpBi ()
TExpBi &	operator= (const TExpBi &)
bool	operator== (const TExpBi &) const
bool	IsExpBiId (const TStr &ExpBiNm, TExpBiId &ExpBiId)
bool	IsExpBiId (const TStr &ExpBiNm)
TExpBiArgType	GetExpBiArgType (const TExpBiId &ExpBiId)
void	AssertArgs (const int &RqArgs, const int &ActArgs)
void	AssertArgValType (const TExpValType &ExpValType, const PExpVal &ExpVal)
PExpVal	GetBiConstVal (const TExpBiId &ExpBiId)
PExpVal	GetBiFuncVal (const TExpBiId &ExpBiId, const TExpValV &ArgValV, const PExpEnv &ExpEnv)
Private Member Functions
void	AddBi (const TStr &ExpBiNm, const TExpBiId &ExpBiId, const TExpBiArgType &ExpBiArgType=ebatUndef)
Private Attributes
TStrIntH	ExpBiNmToIdH
TIntIntH	ExpBiIdToArgTypeH
PExpVal	Val_Undef
PExpVal	Val_True
PExpVal	Val_False
PExpVal	Val_E
PExpVal	Val_Pi

Detailed Description

Definition at line 140 of file exp.h.

Constructor & Destructor Documentation

TExpBi::TExpBi ( )

Definition at line 183 of file exp.cpp.

References AddBi(), TMath::E, ebatFlt, ebatFltFlt, ebatVoid, ebi_Abs, ebi_ACos, ebi_ASin, ebi_ATan, ebi_BinDev, ebi_Ceil, ebi_Cos, ebi_CosH, ebi_E, ebi_Exp, ebi_ExpDev, ebi_False, ebi_Floor, ebi_Frac, ebi_GamDev, ebi_Int, ebi_Log, ebi_Log10, ebi_NrmDev, ebi_Pi, ebi_PoiDev, ebi_Pow, ebi_Sin, ebi_SinH, ebi_Sqr, ebi_Sqrt, ebi_Tan, ebi_TanH, ebi_True, ebi_Undef, ebi_UniDev, ebi_UniDevStep, TExpVal::GetUndefExpVal(), TExpVal::New(), TMath::Pi, Val_E, Val_False, Val_Pi, Val_True, and Val_Undef.

              :
  ExpBiNmToIdH(100), ExpBiIdToArgTypeH(100){
  // constants
  AddBi("Undef", ebi_Undef);
  AddBi("True", ebi_True);
  AddBi("False", ebi_False);
  AddBi("E", ebi_E);
  AddBi("Pi", ebi_Pi);

  // trigonometric funcions
  AddBi("Sin", ebi_Sin, ebatFlt);
  AddBi("Cos", ebi_Cos, ebatFlt);
  AddBi("Tan", ebi_Tan, ebatFlt);
  AddBi("ASin", ebi_ASin, ebatFlt);
  AddBi("ACos", ebi_ACos, ebatFlt);
  AddBi("ATan", ebi_ATan, ebatFlt);
  AddBi("SinH", ebi_SinH, ebatFlt);
  AddBi("CosH", ebi_CosH, ebatFlt);
  AddBi("TanH", ebi_TanH, ebatFlt);

  // exponential functions
  AddBi("Pow", ebi_Pow, ebatFltFlt);
  AddBi("Exp", ebi_Exp, ebatFlt);
  AddBi("Sqr", ebi_Sqr, ebatFlt);
  AddBi("Sqrt", ebi_Sqrt, ebatFlt);
  AddBi("Log", ebi_Log, ebatFlt);
  AddBi("Log10", ebi_Log10, ebatFlt);

  // number manipulation functions
  AddBi("Ceil", ebi_Ceil, ebatFlt);
  AddBi("Floor", ebi_Floor, ebatFlt);
  AddBi("Int", ebi_Int, ebatFlt);
  AddBi("Frac", ebi_Frac, ebatFlt);
  AddBi("Abs", ebi_Abs, ebatFlt);

  // random deviates
  AddBi("UniDev", ebi_UniDev, ebatVoid);
  AddBi("NrmDev", ebi_NrmDev, ebatVoid);
  AddBi("ExpDev", ebi_ExpDev, ebatVoid);
  AddBi("GamDev", ebi_GamDev, ebatFlt);
  AddBi("PoiDev", ebi_PoiDev, ebatFlt);
  AddBi("BinDev", ebi_BinDev, ebatFltFlt);
  AddBi("UniDevStep", ebi_UniDevStep, ebatFltFlt);

  // assign values to constants
  Val_Undef=TExpVal::GetUndefExpVal();
  Val_True=TExpVal::New(double(1));
  Val_False=TExpVal::New(double(0));
  Val_E=TExpVal::New(TMath::E);
  Val_Pi=TExpVal::New(TMath::Pi);
}

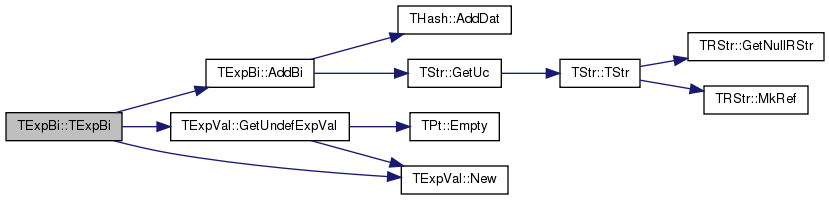
Here is the call graph for this function:

Member Function Documentation

void TExpBi::AddBi	(	const TStr &	ExpBiNm,
		const TExpBiId &	ExpBiId,
		const TExpBiArgType &	ExpBiArgType = `ebatUndef`
	)		`[private]`

Definition at line 235 of file exp.cpp.

References THash< TKey, TDat, THashFunc >::AddDat(), ExpBiIdToArgTypeH, ExpBiNmToIdH, and TStr::GetUc().

Referenced by TExpBi().

                                   {
  ExpBiNmToIdH.AddDat(ExpBiNm.GetUc(), TInt(int(ExpBiId)));
  ExpBiIdToArgTypeH.AddDat(TInt(int(ExpBiId)), TInt(int(ExpBiArgType)));
}

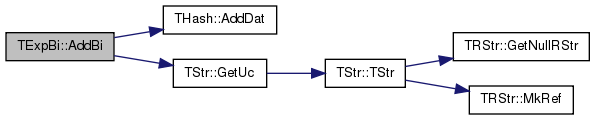
Here is the call graph for this function:

Here is the caller graph for this function:

void TExpBi::AssertArgs	(	const int &	RqArgs,
		const int &	ActArgs
	)

Definition at line 255 of file exp.cpp.

References TExcept::Throw().

Referenced by GetBiFuncVal().

                                                            {
  if (RqArgs!=ActArgs){
    TExcept::Throw("Invalid number of arguments.");
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

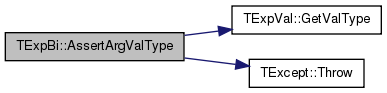
void TExpBi::AssertArgValType	(	const TExpValType &	ExpValType,
		const PExpVal &	ExpVal
	)

Definition at line 261 of file exp.cpp.

References TExpVal::GetValType(), and TExcept::Throw().

Referenced by GetBiFuncVal().

                                                      {
  if (ExpValType!=ExpVal->GetValType()){
    TExcept::Throw("Invalid type of argument.");
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

PExpVal TExpBi::GetBiConstVal ( const TExpBiId & ExpBiId )

Definition at line 268 of file exp.cpp.

References ebi_E, ebi_False, ebi_Pi, ebi_True, ebi_Undef, TExcept::Throw(), Val_E, Val_False, Val_Pi, Val_True, and Val_Undef.

Referenced by TExp::EvalExp().

                                                    {
  switch (ExpBiId){
    case ebi_Undef: return Val_Undef;
    case ebi_True: return Val_True;
    case ebi_False: return Val_False;
    case ebi_E: return Val_E;
    case ebi_Pi: return Val_Pi;
    default: TExcept::Throw("Invalid constant."); return Val_Undef;
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

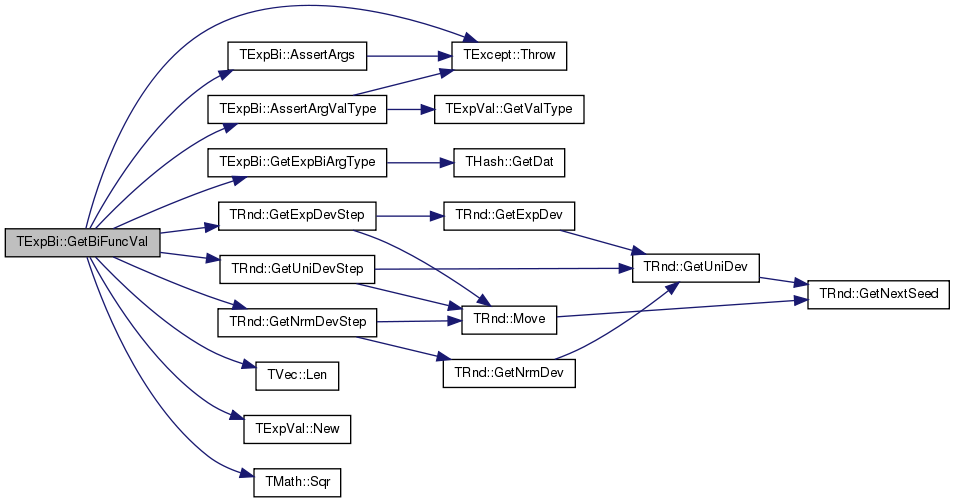
PExpVal TExpBi::GetBiFuncVal	(	const TExpBiId &	ExpBiId,
		const TExpValV &	ArgValV,
		const PExpEnv &	ExpEnv
	)

Definition at line 279 of file exp.cpp.

References AssertArgs(), AssertArgValType(), ebatFlt, ebatFltFlt, ebatUndef, ebatVoid, ebi_Abs, ebi_ACos, ebi_ASin, ebi_ATan, ebi_BinDev, ebi_Ceil, ebi_Cos, ebi_CosH, ebi_Exp, ebi_ExpDev, ebi_ExpDevStep, ebi_Floor, ebi_Frac, ebi_GamDev, ebi_Int, ebi_Log, ebi_Log10, ebi_NrmDev, ebi_NrmDevStep, ebi_PoiDev, ebi_Pow, ebi_Sin, ebi_SinH, ebi_Sqr, ebi_Sqrt, ebi_Tan, ebi_TanH, ebi_UniDev, ebi_UniDevStep, evtFlt, Fail, GetExpBiArgType(), TRnd::GetExpDevStep(), TRnd::GetNrmDevStep(), TRnd::GetUniDevStep(), TVec< TVal >::Len(), TExpVal::New(), TMath::Sqr(), and TExcept::Throw().

Referenced by TExp::EvalExp().

                                                                         {
  TExpBiArgType ExpBiArgType=TExpBi::GetExpBiArgType(ExpBiId);
  int Args=ArgValV.Len();
  double ArgFlt1=0; double ArgFlt2=0;
  switch (ExpBiArgType){
    case ebatUndef: Fail; break;
    case ebatVoid:
      AssertArgs(0, Args); break;
    case ebatFlt:
      AssertArgs(1, Args);
      AssertArgValType(evtFlt, ArgValV[0]);
      ArgFlt1=ArgValV[0]->GetFltVal(); break;
    case ebatFltFlt:
      AssertArgs(2, Args);
      AssertArgValType(evtFlt, ArgValV[0]);
      AssertArgValType(evtFlt, ArgValV[1]);
      ArgFlt1=ArgValV[0]->GetFltVal();
      ArgFlt2=ArgValV[1]->GetFltVal(); break;
    default: Fail;
  }
  PExpVal ExpVal;
  switch (ExpBiId){
    // trigonometric funcions
    case ebi_Sin: ExpVal=TExpVal::New(sin(ArgFlt1)); break;
    case ebi_Cos: ExpVal=TExpVal::New(cos(ArgFlt1)); break;
    case ebi_Tan: ExpVal=TExpVal::New(tan(ArgFlt1)); break;
    case ebi_ASin: ExpVal=TExpVal::New(asin(ArgFlt1)); break;
    case ebi_ACos: ExpVal=TExpVal::New(acos(ArgFlt1)); break;
    case ebi_ATan: ExpVal=TExpVal::New(atan(ArgFlt1)); break;
    case ebi_SinH: ExpVal=TExpVal::New(sinh(ArgFlt1)); break;
    case ebi_CosH: ExpVal=TExpVal::New(cosh(ArgFlt1)); break;
    case ebi_TanH: ExpVal=TExpVal::New(tanh(ArgFlt1)); break;

    // exponential functions
    case ebi_Pow: ExpVal=TExpVal::New(pow(ArgFlt1, ArgFlt2)); break;
    case ebi_Exp: ExpVal=TExpVal::New(exp(ArgFlt1)); break;
    case ebi_Sqr: ExpVal=TExpVal::New(TMath::Sqr(ArgFlt1)); break;
    case ebi_Sqrt: ExpVal=TExpVal::New(sqrt(ArgFlt1)); break;
    case ebi_Log: ExpVal=TExpVal::New(log(ArgFlt1)); break;
    case ebi_Log10: ExpVal=TExpVal::New(log10(ArgFlt1)); break;

    // number manipulation functions
    case ebi_Ceil: ExpVal=TExpVal::New(ceil(ArgFlt1)); break;
    case ebi_Floor: ExpVal=TExpVal::New(floor(ArgFlt1)); break;
    case ebi_Int:{
      double Int; modf(ArgFlt1, &Int);
      ExpVal=TExpVal::New(Int); break;}
    case ebi_Frac:{
      double Frac, Int; Frac=modf(ArgFlt1, &Int);
      ExpVal=TExpVal::New(Frac); break;}
    case ebi_Abs: ExpVal=TExpVal::New(fabs(ArgFlt1)); break;

    // random deviates
    case ebi_UniDev: ExpVal=TExpVal::New(ExpEnv->GetRnd().GetUniDev()); break;
    case ebi_NrmDev: ExpVal=TExpVal::New(ExpEnv->GetRnd().GetNrmDev()); break;
    case ebi_ExpDev: ExpVal=TExpVal::New(ExpEnv->GetRnd().GetExpDev()); break;
    case ebi_GamDev:{
      int ArgInt1=int(ArgFlt1);
      ExpVal=TExpVal::New(ExpEnv->GetRnd().GetGammaDev(ArgInt1)); break;}
    case ebi_PoiDev:{
      ExpVal=TExpVal::New(ExpEnv->GetRnd().GetPoissonDev(ArgFlt1)); break;}
    case ebi_BinDev:{
      int ArgInt2=int(ArgFlt2);
      ExpVal=TExpVal::New(ExpEnv->GetRnd().GetBinomialDev(ArgFlt1, ArgInt2)); break;}
    case ebi_UniDevStep:{
      int ArgInt1=int(ArgFlt1); if (ArgInt1<0){ArgInt1=0;}
      int ArgInt2=int(ArgFlt2);
      ExpVal=TExpVal::New(TRnd::GetUniDevStep(ArgInt1, ArgInt2)); break;}
    case ebi_NrmDevStep:{
      int ArgInt1=int(ArgFlt1); if (ArgInt1<0){ArgInt1=0;}
      int ArgInt2=int(ArgFlt2);
      ExpVal=TExpVal::New(TRnd::GetNrmDevStep(ArgInt1, ArgInt2)); break;}
    case ebi_ExpDevStep:{
      int ArgInt1=int(ArgFlt1); if (ArgInt1<0){ArgInt1=0;}
      int ArgInt2=int(ArgFlt2);
      ExpVal=TExpVal::New(TRnd::GetExpDevStep(ArgInt1, ArgInt2)); break;}

    default: TExcept::Throw("Invalid function.");
  }
  return ExpVal;
}

Here is the call graph for this function:

Here is the caller graph for this function:

TExpBiArgType TExpBi::GetExpBiArgType ( const TExpBiId & ExpBiId )

Definition at line 250 of file exp.cpp.

References ExpBiIdToArgTypeH, and THash< TKey, TDat, THashFunc >::GetDat().

Referenced by GetBiFuncVal().

                                                            {
  TInt ExpBiArgType=ExpBiIdToArgTypeH.GetDat(TInt(int(ExpBiId)));
  return TExpBiArgType(int(ExpBiArgType));
}

Here is the call graph for this function:

Here is the caller graph for this function:

bool TExpBi::IsExpBiId	(	const TStr &	ExpBiNm,
		TExpBiId &	ExpBiId
	)

Definition at line 241 of file exp.cpp.

References ebi_Undef, ExpBiNmToIdH, TStr::GetUc(), and THash< TKey, TDat, THashFunc >::IsKey().

Referenced by IsExpBiId(), and TExp::TExp().

                                                            {
  int ExpBiIdP;
  if (ExpBiNmToIdH.IsKey(ExpBiNm.GetUc(), ExpBiIdP)){
    ExpBiId=TExpBiId(int(ExpBiNmToIdH[ExpBiIdP])); return true;
  } else {
    ExpBiId=ebi_Undef; return false;
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

bool TExpBi::IsExpBiId ( const TStr & ExpBiNm ) [inline]

Definition at line 154 of file exp.h.

References IsExpBiId().

                                     {
    TExpBiId ExpBiId; return IsExpBiId(ExpBiNm, ExpBiId);}

Here is the call graph for this function:

TExpBi& TExpBi::operator= ( const TExpBi & ) [inline]

Definition at line 150 of file exp.h.

References Fail.

{Fail; return *this;}

bool TExpBi::operator== ( const TExpBi & ) const [inline]

Definition at line 151 of file exp.h.

References Fail.

{Fail; return false;}

Member Data Documentation

TIntIntH TExpBi::ExpBiIdToArgTypeH [private]

Definition at line 143 of file exp.h.

Referenced by AddBi(), and GetExpBiArgType().

TStrIntH TExpBi::ExpBiNmToIdH [private]

Definition at line 142 of file exp.h.

Referenced by AddBi(), and IsExpBiId().

PExpVal TExpBi::Val_E [private]

Definition at line 144 of file exp.h.

Referenced by GetBiConstVal(), and TExpBi().

PExpVal TExpBi::Val_False [private]

Definition at line 144 of file exp.h.

Referenced by GetBiConstVal(), and TExpBi().

PExpVal TExpBi::Val_Pi [private]

Definition at line 144 of file exp.h.

Referenced by GetBiConstVal(), and TExpBi().

PExpVal TExpBi::Val_True [private]

Definition at line 144 of file exp.h.

Referenced by GetBiConstVal(), and TExpBi().

PExpVal TExpBi::Val_Undef [private]

Definition at line 144 of file exp.h.

Referenced by GetBiConstVal(), and TExpBi().

The documentation for this class was generated from the following files:

glib-core/exp.h
glib-core/exp.cpp

Public Member Functions

Private Member Functions

Private Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation